Tutorial 链接:Lesson 1 提到的LR背景知识_Omar
PPT Pg-1-56
首先一些历史定义的基本了解:
Trying to get programs to work in a reasonable way to predict stu.
–R. Kohn (2015)
一些定义:
统计:通常是人类的数学模型。
数据挖掘:通常是人类“洞察”的模型。
监督学习:有监督的机器学习:大多数实际的机器学习都使用有监督的学习。 在监督学习中,具有输入变量(x)和输出变量(Y),并使用一种算法来学习从输入到输出的映射函数Y = f(X)。 目标是很好地近似映射函数,以便在拥有新的输入数据(x)时可以预测该数据的输出变量(Y)。监督学习问题可以进一步分为回归和分类问题。(更主流)
非监督学习:没有将输出与真实标签进行比较以评估其性能的基本事实。
当然还有强化学习,半监督学习等。
几何模型:使用来自几何的直觉,例如分离(超)平面,线性变换和距离度量。
概率模型:不同随机变量之间关系的数学模型,通常情况下刻画了一个或多个随机变量之间的相互非确定性的概率关系。
逻辑模型:逻辑数据模型反映的是对数据的观点,是对概念数据模型进一步的分解和细化。
线性回归
线性回归尝试通过将线性方程式拟合到观测数据来模拟两个变量之间的关系。一个变量被认为是解释性变量,另一个被认为是因变量。例如,建模者可能希望使用线性回归模型将个体的体重与其身高相关联。数学角度来看就是最小二乘。
Symbolic :表假设模型,tree,graph
Numeric:表function,NN,Linner equation
回归问题的用处:非线性问题-Swish函数,神经网络-Efficientnet,回归树-决策树DT,KNN
Outcome will be a linear sum of feature values with appropriate weights.
Note: the term regression is overloaded { it can refer to:
The process of determining the weights for the regression equation, or
The regression equation itself.
线性回归线的方程式为Y = a + bX,其中X是解释变量,Y是因变量。线的斜率是b,a是截距。
PPT公式含义:

b是Coefficient,X是解释变量,Y是因变量,整体表达为一个线性的预测。
从结果上来看预测值和实际值之间的差就是误差值。
那么所有点的误差集合就可以用均方误差表示(这里其实还要除n才是均方误差也就是在PPT32页的MSE):
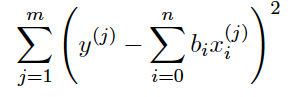
均方误差是指预测值与实际观察值之间的平方差的平均值。 不管它们的方向如何,它只关心平均误差幅度。 但是,由于平方,与偏离实际值的预测相比,远离实际值的预测会受到严重的惩罚。那么我们想要一个好的模型,就要最小化这个MSE。
最小二乘
“最小二乘”方法是一种数学回归分析的形式,用于确定最适合一组数据的线,以可视方式演示数据点之间的关系。 数据的每个点表示一个已知自变量与一个未知因变量之间的关系。
通过最小化曲线上各点的偏移量的平方和(“残差”)来找到与给定点集最匹配的曲线的数学过程。如下图要找到一根到各个点之间直线距离最短的线:

数学概念
Probability: reasons from populations to samples
This is deductive reasoning, and is usually sound (in the logical sense
of the word)
Statistics: reasons from samples to populations
This is inductive reasoning, and is usually unsound (in the logical sense
of the word)
Deductive Reasoning,演绎推理是有效推理的基本形式,前提是保证猜想的真实性,通过假设、观察、证实来得到结论。
Inductive Reasoning,归纳推理,根据已有的结论来推理,通过观察、假设得到理论。
平均数:


f=frequency 一个数字出现的次数。
求期望:


标准差/方差
标准差是方差的平方根

按么标准差的作用就是让我们的方差数据可以更容易被理解。找到一个很好的例子:方差/标准差-例子
协方差Cov和相关系数Corr
用作量化两个连续变量X和Y之间的线性相关性的量度。其值在-1至+1之间变化。


以下引用 https://www.zhihu.com/question/20852004
Cov协方差
可以通俗的理解为:两个变量在变化过程中是同方向变化?还是反方向变化?同向或反向程度如何?
你变大,同时我也变大,说明两个变量是同向变化的,这时协方差就是正的。
你变大,同时我变小,说明两个变量是反向变化的,这时协方差就是负的。
从数值来看,协方差的数值越大,两个变量同向程度也就越大。反之亦然。
相关系数Corr,一种剔除了两个变量量纲影响、标准化后的特殊协方差。
既然是一种特殊的协方差,那它:
1、也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负。
2、由于它是标准化后的协方差,它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度。
课本概念(Corr):
值的符号告诉您关联的方向(正相关,负相关)
数值告诉你的只是数据的分散性
相关性系数不表示任何关系。也就是说,给定一个特定的x,就不能用r值来计算y值
两个数据集有可能具有相同的相关性,但是不同的关系
两个数据集可能有不同的相关性,但是相同的关系
原则:不要用相关性来比较数据集。尽你所能导出的是x,y之间是正的关系还是负的关系
原则:不要用相关性来暗示x导致y
样本和估计
对于相当同质的群体(群体),我们不需要收集大量数据(我们不需要几次啜饮一杯茶来判断它是否太热。)
对于不规则的群体,我们需要对整个群体进行测量,或者 找到一些不必这样做就可以很好地了解群体的方法
抽样是一种得出有关人口结论的方法,无需测量所有人口。结论不必完全准确
没有系统偏差,或者至少没有我们在计算中无法解释的偏差
如果样本与我们试图得出一些结论的人群非常相似,所有这些都是可能的
可计算获得不具代表性样品的可能性(所以,如果这个机会很大,我们可以选择不得出任何结论。)
获得不具代表性的样本的机会随着样本的大小而减少
使用样本估计人口的某些方面是一项常见的任务。除了估算之外,我们还想了解估算的准确性(通常用置信限表示)
从样本中计算出的一些度量是对相应总体值的很好估计。例如,样本均值m是总体均值的一个很好的估计。但情况并非总是如此。例如,样本的范围通常低估了总体的范围
“良好估计”的含义。一个意思是估计值平均是正确的。例如,平均而言,样本的平均值是总体平均值的一个很好的估计值例如,当抽取多个样本并找到每个样本的平均值时,这些平均值的平均值刚好等于总体平均值
这样的估计量被认为是统计上无偏的
回归问题
回归问题是当输出变量是实数或连续值时,例如“工资”或“权重”。 可以使用许多不同的模型,最简单的是线性回归。 它试图使数据适合通过这些点的最佳超平面。
举些例子:
以下哪项是回归问题?
预测一个人的年龄
预测一个人的国籍
预测公司的股价明天是否会上涨
预测文件是否与目击不明飞行物有关?
Ans–预测一个人的年龄。
























 420
420

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








