SML-Abridgelab

Abridgelab

实验背景

本实验主要研究了割边(桥)的寻找算法(Tarjan)以及A*启发式算法

实验细节

1 Bridges

假设有连通图G，e是其中一条边，如果G-e是不连通的，则边e是图G的一条割割边，即桥。此情形下，G-e必包含两个连通分支。

1.1 makeGraph

 makeGraph : edge seq -> ugraph

 type vertex = int
 type edge = vertex * vertex
 type edges = edge seq

 type ugraph = (vertex seq) seq

函数功能：

将所给的边集(Seq形式存储)转换成无向图(ugraph)

函数思路：

首先通过map将所给边集里的所有边映成无向边，然后通过collect整理即可

函数代码：

  fun cmp (x,y) =
  	if x>y then GREATER
  	else if x<y then LESS
  	else EQUAL

  fun makeGraph (E : edge seq) : ugraph = 
  	if length E = 0 then empty()
  	else 
  	let 
  		val firSeq = append (E,(map (fn (x,y) => (y,x)) E))
  		val secSeq = collect cmp firSeq
  		val res = map (fn (x,y) => y) secSeq
  	in 
  		res
  	end

渐进复杂度分析：

firSeq: W=W(append)+W(map)=O(|E|) S=O(1)

secSeq: W=W(collect)=O(|E|log|E|) S=O(log^2|E|)

res: W=O(|V|) S=O(1)

而|E|<=|V|^2

故W(makeGraph)=O(|E|log|V|) S(makeGraph)=O(log^2|V|)

1.2 findBridges

findBridges : ugraph -> edge seq

函数功能：

求出所给无向图中的桥，即割边

函数思路：

对无向图运用Tarjan算法。即：

声明一个长度为全部点的个数的STSeq,其中每个元素均为三元组(isVisited,dfn,low)

分别表示：

isVisted:该点是否被访问过

dfn:在深度优先搜索中该点被访问的次序

low:深度优先搜索中该点可以往回追溯到的最先被访问的点

例如：

1->2->3->4

那么1，2，3，4的dfn分别为0，1，2，3，low则均为0

而本身点由0~|V|-1的整数表示，所以可以一一对应每个点的信息

初始化STSeq之后从给定点开始深度优先搜索，根据搜索到的点的访问与否可分为如下两种情况(假设某次搜索的边为(u,v))：

(1)v未访问

首先v.dfn以及v.low均为v被访问的次序

其次v.low修改为min(v.low,w.low)，w为边(v,w)的终点

(2)v已访问

u.low修改为min(u.low,v.dfn)

注意：由于用(u,v),(v,u)来表示一条无向边，所以需要防止访问过v之后接着访问回u

深搜并修改完每个点的信息之后，对于边(u,v)，如果u.dfn<v.low,那么这条边就是一条割边

函数代码：

  fun findBridges (G : ugraph) : edges = 
  	if length G = 0 then empty() 
  	else
  	let
  		val preSTSeq = STSeq.fromSeq (tabulate (fn _ => (false,0,0)) (length G))
  		fun DFS (fp,p) ((X,pre,label),v) = 
  			case (STSeq.nth X v) of 
  				(true,dfn,low) => 
    				if v=fp then (X,pre,label)
    				else (STSeq.update (p,(true,#2 (STSeq.nth X p),min(#3 (STSeq.nth X p),dfn))) X ,pre,label) 
  				|(false,dfn,low) =>
    				let
    					val X' = STSeq.update (v,(true,label+1,label+1)) X
    					val neighbor = nth G v
    					val (X'',pre',label') = iter (DFS (p,v)) (X',pre,label+1) neighbor
    					val X''' = STSeq.update (p,(true,#2 (STSeq.nth X'' p),min(#3 (STSeq.nth X'' p),#3 (STSeq.nth X'' v)))) X''
    					val p' = STSeq.nth X''' p 
    					val v' = STSeq.nth X''' v
    					val pre'' = if #2 p' < #3 v' then append (pre',singleton (p,v)) else pre' 
    				in
    					(X''',pre'',label')
    				end
  			val res = #2 (DFS (0,0) ((preSTSeq,empty(),0),0))
  	in
  		res
  	end

渐进复杂度分析：

由于采用STSeq存储各点信息，故有对其修改的操作均为常数时间

而割边相对于|E|、|V|很小，故每次发现割边的append操作可忽略

那么该算法时间复杂度即为基于STSeq的深度优先搜索的时间复杂度

即W=S= O(|V| + |E|)

2 Paths “R” Us

2.1 Using Dijkstra’s

2.1.1 Give an example of a graph on ≤ 4 vertices with negative edge weights where Dijkstra’s
algorithm fails to find the shortest paths. List the priority queue operations (i.e. insertions and updates
of shortest path lengths) up to the point of failure. Clearly point out where the algorithm has failed and
what it should have done.

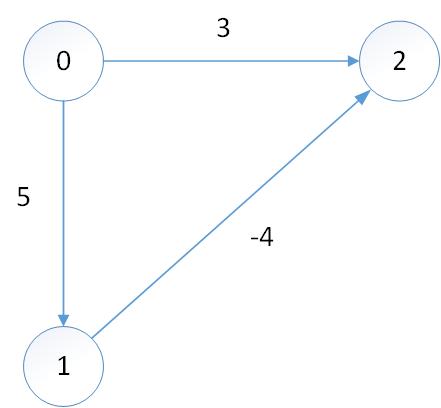
(1)0入队，<(0,0)> | <>

(2)0出队，1,2入队，<(2,3),(1,5)> | <(0,0)>

(3)2出队,<(1,5)> | <(0,0),(2,3)>

(4)1出队,<> | <(0,0),(1,5),(2,3)>

(5)所得0->2路径长为3，显然最短路径应为1，故错误

2.1.2 Assuming there are no negative-weight cycles in G, how would you modify Dijkstra’s
to accomodate negative edge weights and return the correct solution?

使用Bellman-ford算法

2.2 The A ∗ Heuristic

2.2.1 Briefly argue why the Euclidean distance heuristic is both admissible and consistent for
edge weights that represent distances between vertices in Euclidean space.

admissible:由于欧式距离即两点之间的直线距离(即最短距离)，故满足admissible

consistent:对于两点u,v，h(u)<h(v)+E(u,v)<=h(v)+w(u,v)  故满足consistent

2.2.2 Give a heuristic that causes A ∗ to perform exactly as Dijkstra’s algorithm would.

h为常数即可，例如h(v)=0

2.2.3 Give an example of a weighted graph on ≤ 4 vertices with a heuristic that is admissible
but inconsistent, where the Dijkstra-based A ∗ algorithm fails to find the shortest path from a single source
s to a single target t. Label each vertex with its heuristic value, and clearly mark the vertices s and t. In
2-3 clear sentences, explain why the shortest path is not found (e.g., when does the algorithm fail, what
exactly does it do wrong.)

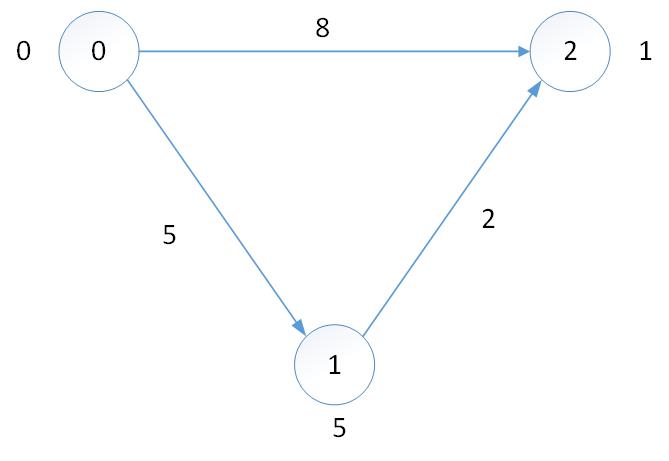
如图，首先(0,0)入队出队后，(2,8+1),(1,5+5)入队，然后(2,8+1)优先出队，使得0->2的最短路径是(0,2)，事

实上最短路径为0->1->2

2.2.4 Give an example of a weighted graph on ≤ 4 vertices with heuristic values that are inadmissible, where

the A ∗ algorithm fails to find the shortest path from a single source to a single target.
Again, clearly label your vertices with heuristic values and explain why the shortest path is not found.

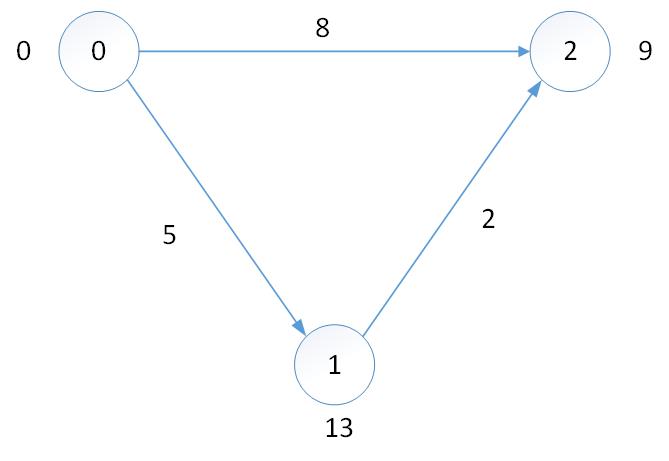
如图，首先(0,0)入队出队后，(2,8+9),(1,5+13)入队，然后(2,8+9)优先出队，使得0->2最短路径为0->2，矛盾。

2.2.5 makeGraph

makeGraph : edge seq -> graph

type graph = (weight Table.table) Table.table

函数功能：

将所给边集转换成邻接表形式

函数思路：

将有向边映成无向边后collect整理即可

函数代码：

  fun makeGraph (E : edge Seq.seq) : graph = 
    let
      val PreL = Seq.map (fn (u,v,w) => (u,Seq.singleton (v,w)) ) E
      val PreR = Seq.map (fn (u,v,w) => (v,Seq.empty ()) ) E
      val Res = Table.collect (Seq.append (PreL,PreR))
    in
      Table.map (fn x => (Table.fromSeq (Seq.flatten x))) Res
    end

渐进复杂度分析：

W= O(|E|log|V|) S=O(log 2 |V|)

2.2.6 findPath

findPath : heuristic -> graph -> (set * set)-> (vertex * real) option

函数功能：

返回所给图中A*启发式算法得出的最短路径

函数思路：

将每次入队的路径长度替换为d(v)+h(v)，之后运用Dijkstra算法即可

函数代码：

  fun findPath h G (S, T) = 
    let
      fun AStar (G, u) =
      let
        fun N(v) =
            case Table.find G v
              of NONE => Table.empty ()
               | SOME nbr => nbr

        fun dijkstra' D Q =
            case PQ.deleteMin Q
              of (NONE, _) => D
               | (SOME (d, v), Q') =>
                 case Table.find D v
                   of SOME _ => dijkstra' D Q'
                    | NONE =>
                      let
                        val insert = Table.insert (fn _ => raise SegmentFault)
                        val D' = insert (v, d) D
                        fun relax (q, (u, w)) = PQ.insert (d+w+h(u)-h(v), u) q
                        val Q'' = Table.iter relax Q' (N v)
                      in dijkstra' D' Q''
                      end
      in
        dijkstra' (Table.empty ()) (PQ.singleton (0.0+h(u), u))
      end
      val pre = Seq.flatten (Seq.map (fn x => Table.toSeq (AStar (G,x))) (Set.toSeq S))
      val res = Seq.filter (fn (x,y) => Set.find T x) pre
    in
      if Seq.length res = 0 then NONE
      else
        SOME (Seq.reduce (fn ((a,b),(c,d)) => if b<d then (a,b) else (c,d)) (#1 (Seq.nth res 0),100000.0) res)
    end

渐进复杂度分析：

上述修改仅为替换，相比较Dijkstra算法多了加减运算，故时间复杂度不变