数学建模笔记——动态规划

---

前言

**动态规划（dynamic programming）**是运筹学的一个分支，是求解决策过程（decision
process）最优化的数学方法。20 世纪 50 年代初 R. E. Bellman 等人在研究多阶段决策过
程(multistep decision process)的优化问题时，提出了著名的最优性原理（principle of
optimality），把多阶段过程转化为一系列单阶段问题，逐个求解，创立了解决这类过程
优化问题的新方法—动态规划。1957 年出版了他的名著《Dynamic Programming》，这
是该领域的第一本著作。

动态规划问世以来，在经济管理、生产调度、工程技术和最优控制等方面得到了广
泛的应用。例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题，用动
态规划方法比用其它方法求解更为方便。

虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题，但是一些与时
间无关的静态规划（如线性规划、非线性规划），只要人为地引进时间因素，把它视为
多阶段决策过程，也可以用动态规划方法方便地求解。

应指出，动态规划是求解某类问题的一种方法，是考察问题的一种途径，而不是
一种特殊算法（如线性规划是一种算法）。因而，它不象线性规划那样有一个标准的数
学表达式和明确定义的一组规则，而必须对具体问题进行具体分析处理。因此，在学习
时，除了要对基本概念和方法正确理解外，应以丰富的想象力去建立模型，用创造性的
技巧去求解。

---

一、简单说动态规划

上文说到动态规划是求解某类问题的一种方法，是考察问题的一种途径，而不是
一种特殊算法，其必须对具体问题进行具体分析处理。举个例子。
如上图，是一个线路网，连线上的数字表示两点之间的距离（或费用）。试寻求一条由 A
到G 距离最短（或费用最省）的路线。

动态规划首先要做的就是对整个过程进行自然划分，通常根据时间顺序或空间顺序特征来划分阶
段，以便按阶段的次序解优化问题，一般用下标k表示第k阶段，上述问题的阶段就是A，B，…，G，。其次，确定每个阶段初始时的状态和允许状态集合，分别用小写xk和大写Xk来表示，还是拿上述问题举例，第二阶段的状态就有B1、B2，第三阶段的状态就有C1、C2、C3、C4。然后当一个阶段的状态确定后，就要做出选择从而演变到下一阶段，这个叫决策，一般用uk表示，Uk则表示允许决策集合，比如当走到B1时，可是选择去C1、C2、C3，这就是决策。

确定好xk和uk等变量后，还需要确定一个状态转移方程和一个指标函数，前者用于更新状态，后者用于评估当前决策的好坏。上述问题的状态转移方程实际上就是一个关于xk的函数：xk+1=uk(xk)，例如uk(B1)=C1,C2,C3。指标函数则是xk和uk(xk)间的数字，记为d(xk, uk(xk))。最后就是确定递归方程和自由终端条件了，一般都长这样：fk(xk)=min(d(xk, uk(xk)) + fk+1(xk+1)), fn+1(xn+1)=0

二、问题求解

1.最短路线问题

具体问题在上面，直接上代码：

# 状态变量x
# 允许状态集合X
X = {
    1: (1,),
    2: (1, 2),
    3: (1, 2, 3, 4),
    4: (1, 2, 3),
    5: (1, 2, 3),
    6: (1, 2),
    7: (1,),
}
# 决策变量u
# 允许决策集合U
U = {
    1: {1: (1, 2)},
    2: {1: (1, 2, 3), 2: (2, 3, 4)},
    3: {1: (1, 2), 2: (1, 2), 3: (2, 3), 4: (2, 3)},
    4: {1: (1, 2), 2: (2, 3), 3: (2, 3)},
    5: {1: (1, 2), 2: (1, 2), 3: (1, 2)},
    6: {1: (1,), 2: (1,)},
    7: {1: ()}
}
# 状态转移方程
# 阶段指标v和指标函数V
v = {
    1: {1: (5, 3)},
    2: {1: (1, 3, 6), 2: (8, 7, 6)},
    3: {1: (6, 8), 2: (3, 5), 3: (3, 3), 4: (8, 4)},
    4: {1: (2, 2), 2: (1, 2), 3: (3, 3)},
    5: {1: (3, 5), 2: (5, 2), 3: (6, 6)},
    6: {1: (4,), 2: (3,)},
    7: {1: (0,)}
}


# 递归方程
def f(k, xk):
    if k == len(v):
        return 0, [(7, 1), ]
    min = 1e06
    for idx, x in enumerate(U[k][xk]):
        tmp = v[k][xk][idx] + f(k + 1, x)[0]
        if tmp < min:
            xx = x
            min = tmp
    return min, [(k, xk), ] + f(k + 1, xx)[1]


R = f(2, 2)
print(f"最短路径为:{R[1][0]}", end='')
for r in R[1][1:]:
    print(f"-->{r}", end='')
print(f", 最短距离为{R[0]}")

结果展示：

2.生产计划问题

工厂生产某种产品，每单位（千件）的成本为 1（千元），每次开工的固定成本为 3
（千元），工厂每季度的最大生产能力为 6（千件）。经调查，市场对该产品的需求量第
一、二、三、四季度分别为 2，3，2，4（千件）。如果工厂在第一、二季度将全年的需
求都生产出来，自然可以降低成本（少付固定成本费），但是对于第三、四季度才能上
市的产品需付存储费，每季每千件的存储费为 0.5（千元）。还规定年初和年末这种产品
均无库存。试制定一个生产计划，即安排每个季度的产量，使一年的总费用（生产成本
和存储费）最少。
上代码：

# 状态变量x
# 允许状态集合X
X = {
    0: [0],
    1: [],
    2: [],
    3: [],
    4: [0]
}
# 决策变量u
# 允许决策集合U
U = [0, 1, 2, 3, 4, 5, 6]
# 状态转移方程
d = [2, 3, 2, 4]
for k in range(4)[::-1][:-1]:
    for u in U:
        for xk_1 in X[k + 1]:
            tmp = xk_1 + d[k] - u
            if tmp >= 0 and tmp not in X[k]:
                X[k].append(tmp)


# 阶段指标v和指标函数V
def v(k, xk, uk):
    if uk > 0:
        return 0.5 * xk + 3 + uk
    else:
        return 0.5 * xk


# 递归方程
def f(k, xk):
    assert xk in X[k]
    if k == len(X) - 1:
        assert xk == 0
        return 0, [(len(X), -1), ]
    min = 1e06
    for xk_1 in X[k + 1]:
        uk = xk_1 + d[k] - xk
        if uk < 0 or uk > 6:
            continue
        tmp = v(k, xk, uk) + f(k + 1, xk_1)[0]
        if tmp < min:
            xxk_1 = xk_1
            u = uk
            min = tmp
    return min, [(k + 1, u), ] + f(k + 1, xxk_1)[1]


R = f(0, 0)
for k, r in enumerate(R[1][:-1]):
    print(f"第{k + 1}季度生产{r[1]}")
print(f"最少费用为{R[0]}")

结果展示：

3.资源分配问题

设某工厂有 1000 台机器，生产两种产品 A、B ，若投入 x 台机器生产 A 产品，则纯收入为5x ，若投入 y 台机器生产 B 种产品，则纯收入为4y ，又知：生产 A 种产品机器的年折损率为 20%，生产 B 产品机器的年折损率为 10%，问在 5 年内如何安排各年度的生产计划，才能使总收入最高？
上代码：

# 状态变量x
# 允许状态集合X
X = {
    0: [1000],
    1: [],
    2: [],
    3: [],
    4: [],
}
# 决策变量u
# 允许决策集合U
U = list(range(1001))
# 状态转移方程
# xk_1 = 0.9 * xk - 0.1 * uk


# 阶段指标v和指标函数V
def v(k, xk, uk):
    return uk + 4 * xk


# 递归方程
def f(k, xk):
    if k == len(X):
        return 0, [(len(X), -1, -1), ]
    max = 0
    for uk in [0, xk]:
        if uk < 0 or uk > xk:
            continue
        xk_1 = 0.9 * xk - 0.1 * uk
        tmp = v(k, xk, uk) + f(k+1, xk_1)[0]
        if tmp > max:
            u = uk
            xxk_1 = xk_1
            max = tmp
    return max, [(k, u, xk), ] + f(k+1, xxk_1)[1]


R = f(0, 1000)
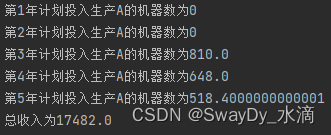
for k, r in enumerate(R[1][:-1]):
    print(f"第{k + 1}年计划投入生产A的机器数为{r[1]}")
print(f"总收入为{R[0]}")

结果展示：

总结

以上就是今天要讲的内容，本文仅仅简单介绍了动态规划，而动态规划其实是一种非常需要丰富想象力，创造力的解决问题的方式，只有深刻理解了相关的概念才能在实际问题中得心应手。一起加油吧！