算法学习03 动态规划-背包问题

OYYHXPJR

已于 2024-03-30 20:29:18 修改

阅读量905

点赞数 17

文章标签：算法学习动态规划

于 2024-01-30 22:59:17 首次发布

本文链接：https://blog.csdn.net/OYYHXPJR/article/details/135928375

版权

背包问题

01背包问题（每件物品最多只能用一次）

#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int v[N];    // 体积
int w[N];    // 价值 
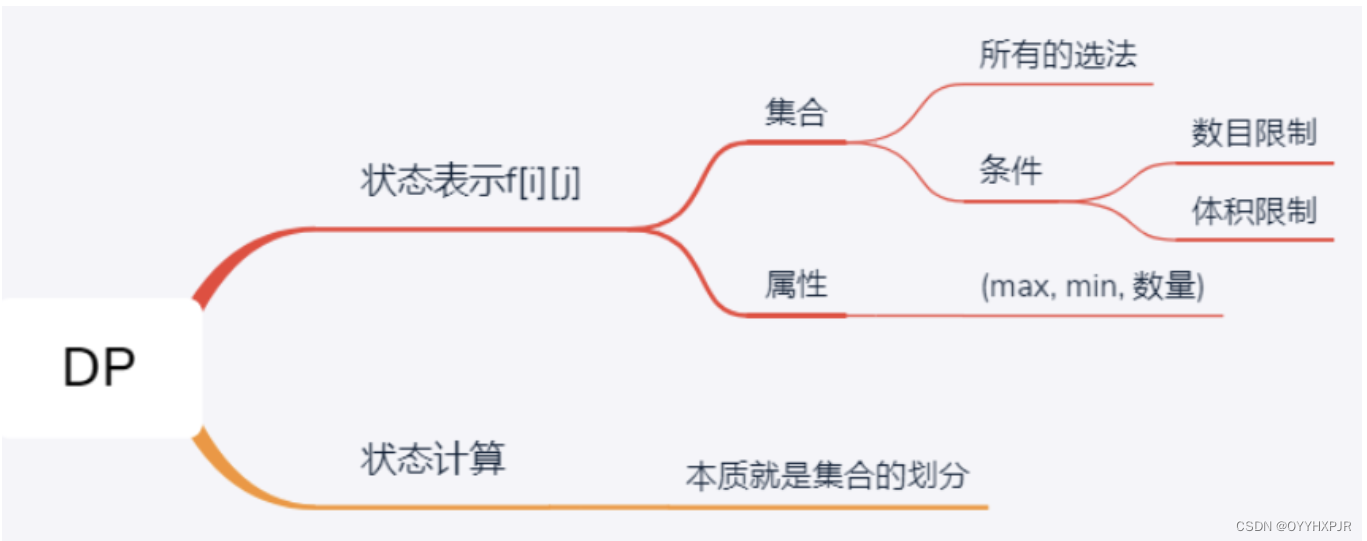
int f[N][N];  // f[i][j], j体积下前i个物品的最大价值 

int main() 
{
    int n, m;   
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }           
    cout << f[n][m] << endl;
    return 0;
}

作者：深蓝
链接：https://www.acwing.com/solution/content/1374/
来源：AcWing

将状态f[i][j]优化到一维f[j]，实际上只需要做一个等价变形。

为什么可以这样变形呢？我们定义的状态f[i][j]可以求得任意合法的i与j最优解，但题目只需要求得最终状态f[n][m]，因此我们只需要一维的空间来更新状态。

（1）状态f[j]定义：N件物品，背包容量j下的最优解。

（2）注意枚举背包容量j必须从m开始。

（3）为什么一维情况下枚举背包容量需要逆序？在二维情况下，状态f[i][j]是由上一轮i - 1的状态得来的，f[i][j]与f[i - 1][j]是独立的。而优化到一维后，如果我们还是正序，则有f[较小体积]更新到f[较大体积]，则有可能本应该用第i-1轮的状态却用的是第i轮的状态。

（4）例如，一维状态第i轮对体积为 3的物品进行决策，则f[7]由f[4]更新而来，这里的f[4]正确应该是f[i - 1][4]，但从小到大枚举j这里的f[4]在第i轮计算却变成了f[i][4]。当逆序枚举背包容量j时，我们求f[7]同样由f[4]更新，但由于是逆序，这里的f[4]还没有在第i轮计算，所以此时实际计算的f[4]仍然是f[i - 1][4]。

如果使用顺序，会先更新f[4],再更新f[7]，对于这个书包问题来讲，就是有可能，在更新f[4]的时候，已经把这次能加的物品加进来了，然后更新f[7]的时候，还有可能再加一次，所以必须使用逆序，保证，f[4]是没有加入新物品前，背包里的最优解。

（5）简单来说，一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」，逆序则不会有这样的问题。

状态转移方程为：f[j] = max(f[j], f[j - v[i]] + w[i] 。

for(int i = 1; i <= n; i++) 
    for(int j = m; j >= 0; j--)
    {
        if(j < v[i]) 
            f[i][j] = f[i - 1][j];  // 优化前
            f[j] = f[j];            // 优化后，该行自动成立，可省略。
        else    
            f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);  // 优化前
            f[j] = max(f[j], f[j - v[i]] + w[i]);                   // 优化后
    }

实际上，只有当枚举的背包容量 >= v[i] 时才会更新状态，因此我们可以修改循环终止条件进一步优化。

for(int i = 1; i <= n; i++)
{
    for(int j = m; j >= v[i]; j--)  //j从最大容量开始枚举，大于等于相应的体积
        f[j] = max(f[j], f[j - v[i]] + w[i]);
}

01背包实战

[NOIP2005 普及组] 采药 - 洛谷

识别模型然后套模板就可以了，这个题的T（限制的采药时间相当于是背包的体积），M（药的种类数相当于是背包可以选的种类数）

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int m, n;
int f[N];

int main()
{
    cin >> m >> n;//别输入反了，n是个数，m是背包的体积
    for (int i = 0; i < n; i ++ )
    {
        int v, w;
        cin >> v >> w;
        for (int j = m; j >= v; j -- )
            f[j] = max(f[j], f[j - v] + w);
    }

    cout << f[m] << endl;

    return 0;
}

01背包稍微变形

小A点菜 - 洛谷

变点：1、初始化f[0]=1 2、状态转移方程（一维）f[j]+=f[j-v[i]];

当前钱数的方案数 就等于 当前钱数的方案数 与 当前钱数减去菜价所剩钱数的方案数 的和

#include<iostream>
using namespace std;
const int N=2e4+10;
int n,m;
int v[N],w[N];
int f[N];//恰好花费i元的方案数
int main()
{
    //n是物品个数，m是背包容量
    cin>>n;cin>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>v[i];
    }
    f[0]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]+=f[j-v[i]];
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

完全背包（每件物品有无限个）

虽然形式上好像只有一行不一样，但是原理其实完全不一样

f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]); 01背包

f[i][j]= max(f[i][j], f[i][j-v[i]]+w[i]); 完全背包

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;

int f[N];
int v[N],w[N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            if(j-v[i]>=0)
            {
                f[j]=max(f[j],f[j-v[i]]+w[i]);
            }
        }
    }
    cout << f[m]<<endl;
    
    // for(int i = 1 ; i <=n ;i++)
    //     for(int j = 0 ; j <=m ;j++)
    //         {
    //             f[i][j] = f[i-1][j];
    //             if(j-v[i]>=0)
    //             f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
    //         }
    // cout<<f[n][m];
    return 0;
}

完全背包稍微变形的题目

1371. 货币系统 - AcWing题库

这个题一看就知道是完全背包，因为货币可以用无限次，然后求的是“凑法”，最需要动脑子的是这个转移方程的变形：f[j]+=f[j-v[i]];

//完全背包
#include <iostream>
#include <cstring>
#include <algorithm>
typedef long long LL;


using namespace std;

const int N = 1e5+10;

LL f[N];
LL v[N],w[N];

int main()
{
    int n,m;
    cin>>n>>m;
    f[0]=1;
    for(int i=1;i<=n;i++)cin>>v[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=v[i];j<=m;j++)
        {
        f[j]+=f[j-v[i]];
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

蓝桥杯真题

1226. 包子凑数 - AcWing题库

只不过这个题还结合了最大公约数的知识，如果这一系列数的最大公约数不是1，那么有INF种情况凑不出来（这个我没有想到）

这里完全背包的状态转移方程为：f[j]=f[j]|f[j-v[i]];//f[i]表示i能不能被凑出来，bool类型

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 10010;

int f[N];
int v[N];
int gcd(int a, int b)  // 欧几里得算法
{
    return b ? gcd(b, a % b) : a;
}


int main()
{
    int n;//物体个数 背包容量
    cin>>n;
    for(int i=1;i<=n;i++)cin>>v[i];
    int g=v[1];
    for(int i=2;i<=n;i++)
    {
        g=gcd(g,v[i]);
    }
    if(g!=1)cout<<"INF"<<endl;
    else
    {
        f[0]=1;
        for(int i=1;i<=n;i++)
        {
            for(int j=v[i];j<N;j++)
            {
                f[j]=f[j]|f[j-v[i]];
            }
        }
        int ans=0;
        for(int i=1;i<N;i++)
        {
            if(f[i]==0)ans++;
        }
        cout<<ans<<endl;
    }

    // for(int i = 1 ; i <=n ;i++)
    //     for(int j = 0 ; j <=m ;j++)
    //         {
    //             f[i][j] = f[i-1][j];
    //             if(j-v[i]>=0)
    //             f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
    //         }
    // cout<<f[n][m];
    return 0;
}

多重背包（也就是有数量限制的完全背包）

朴素版本的多重背包（三重循环，k满足两个条件）

#include<bits/stdc++.h>
using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];//前i个数  总体积不超过j


int main()
{

	cin >> n >> m;//物品数量和背包体积
	for (int i = 1; i <= n; i++)
	{
		cin >> v[i] >> w[i]>>s[i];//第i件物品的体积 价值 数量
	}
	
	for(int i=1;i<=n;i++)
	{
	    for(int j=0;j<=m;j++)//j是说总体积不超过j，m是背包的体积
	    {
	        for(int k=0;k*v[i]<=j&&k<=s[i];k++)
	        {
	            f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
	        }
	    }
	}
	cout << f[n][m] << endl;

	return 0;
}

用二进制优化的多重背包（我还没完全搞懂）

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 25000;
const int M=2010;
int v[N],w[N];
int f[M];

int main()
{
    int n,m;
    cin>>n>>m;
    int cnt=0;//分的组数
    
    for(int i=1;i<=n;i++)
    {
        int a,b,s;
        cin>>a>>b>>s;
        int k=1;//k是当前这组的个数 1 2 4 8 
        while(k<=s)
        {
            cnt++;
            v[cnt]=a*k;//当前这组的总种类
            w[cnt]=b*k;//当前这组的总重量
            s-=k;
            k*=2;
        }
        if(s>0)
        {
            cnt++;
            v[cnt]=a*s;
            w[cnt]=b*s;
        }
    }
    
     n = cnt ; //枚举次数正式由个数变成组别数
        
        for(int i=1;i<=n;i++)
        {
            for(int j=m;j>=v[i];j--)
            {
                f[j]=max(f[j],f[j-v[i]]+w[i]);
            }
        }
    
    cout<<f[m];
    return 0;
}

分组背包

转移的时候如果用的是上一层的状态，那就从大到小来枚举体积；如果用的是本层的，那就从小到大枚举体积

二维做法

#include<bits/stdc++.h>
using namespace std;

const int N=110;
int f[N][N];  //只从前i组物品中选，当前体积小于等于j的最大值
int v[N][N],w[N][N],s[N];   //v为体积，w为价值，s代表第i组物品的个数
int n,m,k;

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>s[i];
        for(int j=0;j<s[i];j++){
            cin>>v[i][j]>>w[i][j];  //读入
        }
    }

    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            f[i][j]=f[i-1][j];  //不选
            for(int k=0;k<s[i];k++){
                if(j>=v[i][k])     f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);  
            }
        }
    }
    cout<<f[n][m]<<endl;
}

因为只用到了第i-1列，所以可以仿照01背包的套路逆向枚举体积（转移的时候如果用的是上一层的状态，那就从大到小来枚举体积；如果用的是本层的，那就从小到大枚举体积）

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 110;
int v[N][N],w[N][N];
int s[N];
int f[N];

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>s[i];
        for(int j=0;j<s[i];j++)
        {
            cin>>v[i][j]>>w[i][j];
        }
    }
    
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=0;j--)
        {
            for(int k=0;k<s[i];k++)
            {
                if(j>=v[i][k])
                {
                    f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
                }
            }
        }
    }
    
    cout<<f[m]<<endl;
    
    return 0;
}

背包思维的题（状态变化）

3417. 砝码称重 - AcWing题库

AcWing 3417. 砝码称重(闫式dp/dfs) - AcWing，这篇题解写的相当清楚

#include <bits/stdc++.h>

using namespace std;

const int N = 110, M = 2e5 + 10;
int sum;
int n;
int w[N];
bool f[N][M];

int main() {

    cin>>n;
    for (int i = 1; i <= n; i++)
    {
        scanf("%d", &w[i]);
        sum+=w[i];
    }

    f[0][0]=true;
    for (int i = 1; i <= n;i++)
        for (int j = 0; j <=sum;j++)
            f[i][j]=f[i-1][j]||f[i-1][j+w[i]]||f[i-1][abs(j-w[i])];
                //只要有一个非空,f[i][j]就非空
    
    int ans = 0;
    for (int i = 1; i <=sum;i++)
    if(f[n][i])ans++;//不为零说明可以选出这个质量的砝码

    cout << ans;

    return 0;
}

OYYHXPJR

关注

17
点赞
踩
24

收藏

觉得还不错? 一键收藏
1
评论
算法学习03 动态规划-背包问题

（4）例如，一维状态第i轮对体积为 3的物品进行决策，则f[7]由f[4]更新而来，这里的f[4]正确应该是f[i - 1][4]，但从小到大枚举j这里的f[4]在第i轮计算却变成了f[i][4]。如果使用顺序，会先更新f[4],再更新f[7]，对于这个书包问题来讲，就是有可能，在更新f[4]的时候，已经把这次能加的物品加进来了，然后更新f[7]的时候，还有可能再加一次，所以必须使用逆序，保证，f[4]是没有加入新物品前，背包里的最优解。将状态f[i][j]优化到一维f[j]，实际上只需要做一个等价变形。
复制链接

扫一扫