深度学习框架中的自动微分及高阶导数

OneFlow深度学习框架

已于 2022-04-22 08:40:52 修改

阅读量4.5k

点赞数 3

分类专栏：前沿技术文章标签：深度学习神经网络人工智能算法 python

于 2022-04-19 08:03:00 首次发布

本文链接：https://blog.csdn.net/OneFlow_Official/article/details/124287755

版权

本文介绍了深度学习中高阶导数的计算方法，特别是自动微分的反向模式和前向模式。通过PyTorch示例展示了如何计算Hessian矩阵及其与Hessian向量积（HVP）的关系。自动微分是理解反向传播和前向传播的关键，用于高效计算神经网络的梯度。Hessian矩阵在优化和判断极值点时起重要作用，但由于其规模，通常需要避免直接计算。最后，文章提到了Taylor模式用于高效求解高阶导数的策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

撰文 | 大缺弦

1、高阶导数是怎么样的

先看一个 Stackoverflow 上关于如何用 PyTorch 计算高阶导数的最高票回答（https://stackoverflow.com/questions/50322833/higher-order-gradients-in-pytorch）：

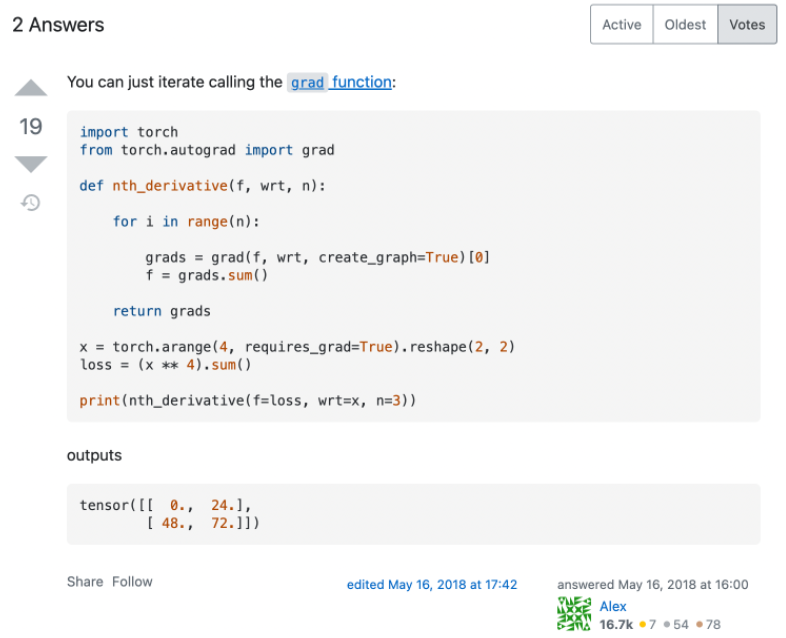
代码很简洁，结果看起来也是对的，然而实际上这个做法是有很大问题的，只是对于作者所测试的这类函数碰巧适用而已。

那高阶导数实际上又该怎么计算呢？

这个问题的标准答案可能是：要看想计算的高阶导数是什么样的。平常的神经网络训练中，我们想让 loss 下降，也就是将 loss 作为损失函数”，所以求出一阶导数、 ......也就是 w1_grad、w2_grad......，并用它来更新 w1、w2......如果我们现在有一个需求：想通过更新 w1、w2......来让反向传播得到的 w1_grad 尽可能低，也就是将 w1_grad 作为损失函数（在训练一些 GAN 网络时，不希望梯度的绝对值太大，就会有类似的需求），所以要计算、......也就是二阶导数、......

这可以用下面的 PyTorch 代码来简单的实现：

import torch
x = ...
loss = model(x)
w1_grad = torch.autograd.grad(outputs=loss, inputs=model.w1, create_graph=True)
w1_grad.backward()

不过，在大部分场景中想计算的二阶导数是另一种形式：

这个矩阵叫做 Hessian 矩阵。它是正儿八经的 “函数 loss = f(W) 的二阶导数”，即将神经网络看作一个输入为所有权重、输出为 loss 的多输入、单输出的函数 f （注意这里的输入不包括训练数据，因为训练数据实际上是固定的，是整个训练集，神经网络的训练就是通过改变 W 使在给定的训练集下的 loss 最低），对该函数 f 求导、再求导得到的结果。

它可以用来判断某个 W 有没有让 loss 处于极小值点、极大值点或鞍点，它也是对 f(W) 做泰勒展开后二次项的系数的两倍，所以当我们想用一个二次函数来模拟神经网络，并根据二次函数的性质来更新 W、优化 loss 的时候（这个叫作牛顿法），也是一个绕不开的概念。在很多场景，例如常用的优化方法共轭梯度法之中，这个矩阵还会和一个向量相乘，被称为 HVP（Hessian-Vector Product)。

那么这个 Hessian 矩阵以及 HVP 该怎么求？一个容易想到的方法是：考虑到在上面那个希望尽可能低的场景里，我们求出的、