【Attention优化重大突破！显存减半效率倍增，大模型长文本处理迎来新时代】

本文链接：https://blog.csdn.net/OneThingAI/article/details/146238996

一，前言

从Transformer 17年被提出来， Attention 层的相关的工作从未间断，参考邱锡鹏教授21年关于Transformer的综述里的整理如下：

更耳熟能详一些的如：MQA，GQA ，DeepSeek的MLA，阶跃星辰的MFA，以及最近DeepSeek提出的NSA和Kimi提出的MoBA。

到底这么多的Attention为什么被提出，它们都意图解决什么问题。我们用接下来的两个章节来解释一下。

二，Attention 是什么

为了更容易理解我们接下来的内容，我们先来看一下Attention的计算公式：

这个公式到底在做什么，flashattention的论文里说的比较清楚：

结合下图更有利于我们深入的理解attention（11. Self Attention - by Tom Yeh - AI by Hand ✍️）

下面会对以上的这张图做分块的解释：

语言模型简单来说就是针对输入的序列计算概率，推测下一个token是什么，新生成的token以及历史上所有的token又做为下一轮生成的输入。上面这个图是模型多层transformer中的一层的计算过程的具象化展示，主要含有Attention和FFN（MLP）这2个子层。下面几个小节主要解释attention的计算部分。

1，我们假设该图是transformer第一层，每个token是一个词，这样可以简化讨论。假设有4个词做为输入，被转化为4个向量，也就是图里的Features：x1，x2，x3，x4。通过和模型的权重矩阵Wq，Wk 相乘，得到一个Q矩阵，也就是图里的q1，q2，q3，q4 这4个销向量。得到一个K矩阵也就是k1，k2，k3，k4 这4个销向量；

2， Q，K 通过矩阵乘法计算得到一个矩阵S

3，然后通过softmax 等计算得到矩阵P

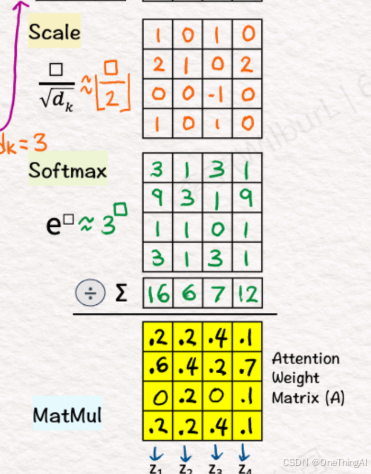
4，输入x1，x2，x3，x4通过和模型的权重矩阵Wv相乘得到v1，v2，v3，v4 也就是矩阵V。最后矩阵P和V相乘得到最终的输出向量z1，z2，z3，z4，也就是矩阵O

三，为什么能做和要做前言里提到的优化工作

从第二章节不难看出（Decoder-only的attention计算和上面略有不同，不影响计算复杂度讨论），如果不做任何优化，生成每一个token的计算复杂度是O(n^2)，最终生成的序列全局计算复杂度是O(n^3)。对于上下文这个计算复杂度肯定是无法接受的。

1，所以，直觉上提升Attention的性能的做法是降低它的计算复杂度.

kv caching就是为了解决这个问题将单个token的计算复杂度降低到O(n) （n为当前序列长度），全局的复杂度就下降到O(n^2)极大的提升了性能。比如下图开不开起kv caching 作者观察到的。 kv caching 是一个空间换时间的做法，那么我们需要付出的就是更多的显存空间用来做k，v 的缓存。

kv caching 为什么可行参考下面2个图（https://x.com/_avichawla/status/1890288542322221206）：

大体来说就是Decoder 里的attention计算由于当前token只参考之前的token而不向后参考，所以如第二章节的历史上的z向量可以在新token生成时不更新，Zk = (Qk * K) * V。

2，kv caching 极大的提升了性能，但是需要大量的cache 空间。比如上图所示看Llama3 70B，4k token需要10.5 GB 的cache空间，这个是极大的开销。为了降低cache的压力，开头提到的MQA，GQA等被提出，通过降低k v 的数量来降低对显存的消耗。同时模型能力没有出现明显的下降，所以得到了广泛的使用。DeepSeek 的MLA 则是通过压缩k v 大小的方式，进一步降低了cache 的压力，这里的风险是信息的损失会导致模型性能的下降，但从实际的结果来看，这个风险目前被处理得很好。

3，即使做了1，2的优化，问题就不存在了吗？当然不是，对于更长的上下文cache的压力还是很大，计算压力还是O(n^2) （n 为序列长度），这样模型实际是很难继续朝着长上下文scaling的。2和其他的一些研究表attention是稀疏的，序列越长attention越稀疏，像DeepSeek 的NSV，Kimi的MoBA以及别的一些研究就诞生了，通过这些研究我们可以进一步降低计算量和cache大小同时不降低模型性能。