二叉搜索树 2016.4.11

一、定义

二叉搜索树（Binary Search Tree）（BST）（又：二叉查找树，二叉排序树）

递归的定义：

它或者是一棵空树

或者是具有下列性质的二叉树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值

它的左、右子树也分别为二叉排序树

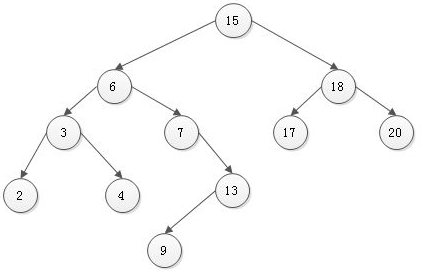
例：

二、模版

#include <iostream>
#include <cstdlib>
#include <cstdio>

using namespace std;

typedef int KeyType;

typedef struct BST {
    KeyType key;    //关键字
    BST* left;      //左孩子指针
    BST* right;     //右孩子指针
    BST* parent;    //指向父节点指针
}BST, *bst;

void Insert(bst* root, KeyType key);
bst Search(bst root, KeyType key);
bst Search_Min(bst root);
bst Search_Max(bst root);
bst Search_Pre(bst pre);
bst Search_Next(bst next);
bool Delete(bst* root, KeyType key);
void Create(bst* root, KeyType *keyArray, int len);

int main()
{
    bst root = NULL;
    KeyType nodeArray[11] = {15, 6, 18, 3, 7, 17, 20, 2, 4, 13, 9};
    Create(&root, nodeArray, 11);
    for (int i=0; i<2; ++i) {
        Delete(&root,nodeArray[i]);
    }
    printf("%d\n", Search_Pre(root)->key);
    printf("%d\n", Search_Next(root)->key);
    printf("%d\n", Search_Min(root)->key);
    printf("%d\n", Search_Max(root)->key);
    printf("%d\n", Search(root,13)->key);
    return 0;
}

//插入
//可能要改变根结点的地址，所以传的是二级指针
void Insert(bst* root, KeyType key)
{
    bst t = (bst)malloc(sizeof(BST));
    t->key = key;
    t->left = t->right = t->parent = NULL;

    if ((*root) == NULL) {
        *root = t;
        return;
    }
    //插入到当前结点（*root）的左孩子
    if((*root)->left == NULL && (*root)->key > key){
        t->parent = (*root);
        (*root)->left = t;
        return;
    }
    //插入到当前结点（*root）的右孩子
    if((*root)->right == NULL && (*root)->key < key){
        t->parent = (*root);
        (*root)->right = t;
        return;
    }
    if (key == (*root)->key) {
        return;
    } else if (key < (*root)->key) {
        Insert(&((*root)->left), key);
    } else {
        Insert(&((*root)->right), key);
    }
}

//查找元素,找到返回关键字的结点指针，没找到返回NULL
bst Search(bst root, KeyType key)
{
    if(root == NULL) {
        return NULL;
    } else if (key < root->key) {
        return Search(root->left, key);
    } else if (key > root->key) {
        return Search(root->right, key);
    } else {
        return root;
    }
}

//查找最小关键字,空树时返回NULL
bst Search_Min(bst root)
{
    if (root == NULL) {
        return NULL;
    } else if (root->left == NULL) {
        return root;
    } else {
        return Search_Min(root->left);
    }
}

//查找最大关键字,空树时返回NULL
bst Search_Max(bst root)
{
    if (root == NULL) {
        return NULL;
    } else if (root->right == NULL) {
        return root;
    } else {
        return Search_Max(root->right);
    }
}

//查找某个结点的前驱
bst Search_Pre(bst pre)
{
    if(pre == NULL) {       //空树
        return pre;
    } else if(pre->left) {  //有左子树、左子树中最大的那个
        return Search_Max(pre->left);
    } else {                //无左子树,查找某个结点的右子树遍历完了
        if (pre->parent == NULL) {
            return NULL;
        }
        while (pre) { //向上寻找前驱
            if (pre->parent->right == pre) {
                break;
            }
            pre = pre->parent;
        }
        return pre->parent;
    }
}

//查找某个结点的后继
bst Search_Next(bst next)
{
    if(next == NULL) {  //空树
        return next;
    } if (next->right) {//有右子树、右子树中最小的那个
        return Search_Min(next->right);
    } else {            //无右子树,查找某个结点的左子树遍历完了
        if (next->parent == NULL) {
            return NULL;
        }
        while (next){    //向上寻找后继
            if (next->parent->left == next) {
                break;
            }
            next = next->parent;
        }
        return next->parent;
    }
}

//根据关键字删除某个结点,删除成功返回true,否则返回false
//如果把根结点删掉，那么要改变根结点的地址，所以传二级指针
bool Delete(bst* root, KeyType key)
{
    bst q;
    bst p = Search(*root, key); //查找到要删除的结点
    KeyType temp;               //暂存后继结点的值
    if (p == NULL) {                                     //没查到此关键字
        return false;
    } else if (p->left == NULL && p->right == NULL) {    //1.被删结点是叶子结点，直接删除
        //只有一个元素，删完之后变成一颗空树
        if (p->parent == NULL){
            free(p);
            (*root) = NULL;
        } else {
            //删除的结点是父节点的左孩子
            if (p->parent->left == p) {
                p->parent->left = NULL;
            }
            else {//删除的结点是父节点的右孩子
                p->parent->right = NULL;
            }
            free(p);
        }
    } else if (p->left && !(p->right)) {                 //2.被删结点只有左子树
        p->left->parent = p->parent;
        //如果删除是父结点，要改变父节点指针
        if (p->parent == NULL) {
            *root=p->left;
        }
        //删除的结点是父节点的左孩子
        else if (p->parent->left == p) {
            p->parent->left = p->left;
        }
        else {//删除的结点是父节点的右孩子
            p->parent->right=p->left;
        }
        free(p);
    } else if (p->right && !(p->left)) {                 //3.被删结点只有右孩子
        p->right->parent = p->parent;
        //如果删除是父结点，要改变父节点指针
        if (p->parent == NULL) {
            *root=p->right;
        }
        //删除的结点是父节点的左孩子
        else if (p->parent->left == p) {
            p->parent->left=p->right;
        }
        //删除的结点是父节点的右孩子
        else {
            p->parent->right=p->right;
        }
        free(p);
    }
                                                         //4.被删除的结点既有左孩子，又有右孩子
                                                         //该结点的后继结点肯定无左子树(参考上面查找后继结点函数)
                                                         //删掉后继结点,后继结点的值代替该结点
    else {
        //找到要删除结点的后继
        q = Search_Next(p);
        temp = q->key;
        //删除后继结点
        Delete(root, q->key);
        p->key = temp;
    }
    return true;
}

//创建一棵二叉查找树
void Create(bst* root, KeyType *keyArray, int len)
{
    //逐个结点插入二叉树中
    for(int i=0; i<len; ++i) {
        Insert(root, keyArray[i]);
    }
}

转自
http://blog.csdn.net/touch_2011/article/details/6831924
略有改动