顶点着色问题

今天一个本科小学弟问到一个matlab编程问题，说自己只是改了别人的一小段代码，结果程序运行就通不过。给他看了一遍代码，我也没有发现问题。在一个for循环里面，第一遍能跑完，跑到第二遍的时候就会在一句调用$sum$函数的地方提示错误，反复对比单步调试无果。还多次确认，$sum$函数本身并没有什么使用限制。后来突然灵光一闪，发现他的for循环里面用到一个变量名就叫 sum， 第一遍循环跑完后，sum变量进入工作空间，第二遍的时候，matlab只知道sum是个变量名，而小学弟的意图却是想调用$sum$函数。编程习惯不好害师兄啊。

然而我们今天要讲的却是程序中另外一个问题——顶点着色问题。回来仔细查找资料后，才发现这个顶点着色问题属于图论里面的一个小分支。可以在维基百科里面看到图的着色问题详细的介绍(https://en.wikipedia.org/wiki/Graph_coloring)。

顶点着色问题 vertex coloring

维基里面讲得很清楚了，图的着色问题可以退化到边的着色问题，边的着色问题可以退化到点的着色问题(vertex coloring)。

问题来源——四色问题

图的着色是由地图的着色问题引申而来：用$m$种颜色为地图着色，使得地图上的每一个区域着一种颜色，且相邻区域颜色不同。四色问题：“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”

顶点着色问题的基本概念

$m$可着色：若一个图最少需要$m$种颜色才能使图中每条边连接的两个顶点着不同的颜色，则称$m$为该图的色数。求$m$的问题称为图的$m$可着色优化问题。

独立集：对图$G=(V,E)$，设$S$是$V$的一个子集，其中任意两个顶点在$G$中均不相邻，则称$S$为$G$的一个独立集。

最大独立集：如果$G$不包含适合$|S'|>|S|$的独立集$S'$，则称$S$为$G$的最大独立集。

极大覆盖：设$K$是$G$的一个独立集，并且对于$V-K$的任一顶点$v$, $K+v$都不是$G$的独立集，则称$K$是$G$的一个极大覆盖。

极小覆盖：极大独立集的补集称为极小覆盖。

$V$的子集$K$是$G$的极小覆盖当且仅当：对于每个顶点$v$或者$v$属于$K$,或者$v$的所有邻点属于$K$（但两者不同时成立）。

顶点着色的算法思想

显然，同色顶点集实际上是一个独立集，当用第1种颜色上色时，为了尽可能扩大颜色1的顶点个数，逼近所用颜色数最少的目的，事实上就是找出图$G$的一个极大独立集并给它上色1。用第2种颜色上色时，同样选择另一个极大独立集上色，$\dots$，当所有顶点涂色完毕，所用的颜色数即为所选的极大独立集的个数。

需要说明的是，上述其和能够包含所有顶点的极大独立集个数未必唯一。

顶点着色问题的常用算法

回溯算法、分支定界法、Welsh Powell法、布尔代数法、蚁群算法、贪婪算法、禁忌搜索算法、神经网络、遗传算法以及模拟退火算法等都可以用来解决着色问题。（然而到现在我还是一个都不会）

通常解决着色问题的算法采用暴力法、贪婪法、深度优先、广度优先等思想可以优解，但显然时间复杂性太大，如回溯算法的时间复杂度为指数阶的；而Welsh-Powell算法和贪婪算法理论上都可以在多项式时间内得到可行解，然而却并不是最优解。

现在先讲一下Welsh-Powell法和贪婪法。
穷举法-Welsh-Powell着色法

• I. 将图$G$中的结点按度数递减顺序排序（可能不唯一，结点数相同的点可能有多个）
• II. 用第一种颜色对第一结点着色，并按排列顺序对与前面着色结点不相邻的每一结点着上相同的颜色。
• III. 用第二种颜色对尚未着色的结点重复II，用第三种颜色继续这种做法，直到所有的结点全部着上色为止。

贪心法
贪心策略：选择一种颜色，以任意顶点作为开始顶点，依次考察图中的未被着色的各个顶点，如果一个顶点可以用颜色1着色，换言之，该顶点的邻接点都还未被着色，则用颜色1为该顶点着色；当没有顶点能以这种颜色着色时，选择颜色2和一个未被着色的顶点作为开始顶点，用第二种颜色为尽可能多的顶点着色，如果还有未着色的顶点，则选取颜色3并为尽可能多的顶点着色，依此类推。

贪婪算法实现顶点着色问题的matlab程序

在这里，我就贴一个自己的贪婪算法。

% --- 贪婪算法实现顶点着色问题 ---
clear; 
clc;

graph = [                     % 共A、B、C、D、E、F、G、H，8个点的图
%   A B C D E F G H    
    0 1 1 1 0 0 1 0;          % A
    1 0 1 1 1 0 0 0;          % B
    1 1 0 0 1 1 1 0;          % C
    1 1 0 0 1 0 1 0;          % D
    0 1 1 1 0 1 1 1;          % E
    0 0 1 0 1 0 0 1;          % F
    1 0 1 1 1 0 0 1;          % G
    0 0 0 0 1 1 1 0;          % H
    ];
vnum = max(size(graph));
colorTbl = zeros(1, vnum);    % 着色方案表,0代表未着色 

cInd = 1;
while sum(colorTbl==0) > 0                              % 全部着色完成
    for vInd = 1 : vnum
        if 0 == colorTbl(vInd)                          % 当前顶点vInd尚未着色
            tmpTbl = colorTbl(graph(:, vInd)~=0);       % 当前顶点vInd的邻接点的着色表
            if 0 == sum(tmpTbl==cInd)                   % vInd的邻接点都尚未着当前色cInd
                colorTbl(vInd) = cInd;                  % 顶点vInd着色cInd
            end
        end
    end
    cInd = cInd + 1;
end

运行以上程序，结果如下：

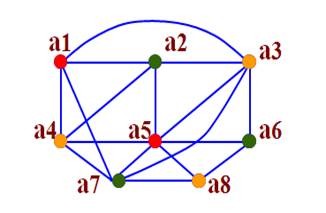
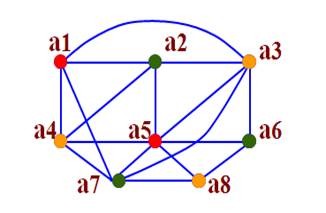
也就是说点 A-E着第一种颜色，B-F-G着第二种颜色，C-D-H着第三种颜色。
结果和开篇的第二张图完全一致。

把上面代码中的图$graph$换成一个更复杂一点的图如下：

graph = [
%   A B C D E F G H I J    
    0 1 0 0 1 0 1 0 0 0;        % A
    1 0 1 0 0 0 0 1 0 0;        % B
    0 1 0 1 0 0 0 0 1 0;        % C
    0 0 1 0 1 0 0 0 0 1;        % D
    1 0 0 1 0 1 0 0 0 0;        % E
    0 0 0 0 1 0 0 1 1 0;        % F
    1 0 0 0 0 0 0 0 1 1;        % G
    0 1 0 0 0 1 0 0 0 1;        % H
    0 0 1 0 0 1 1 0 0 0;        % I
    0 0 0 1 0 0 1 1 0 0;        % J
    ];

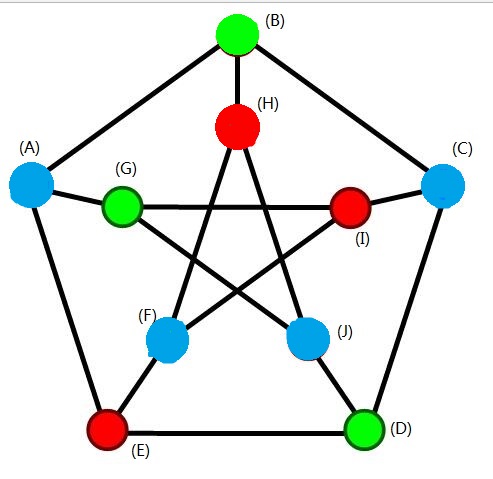
程序运行结果如下：

与以上结果也完全一致。但是显然当点的规模增大后，程序的时间复杂度会呈指数级别上升。还是学会其他更优的解法好。