动态规划---例题5.凸多边形最优三角剖分问题

一.题目描述

通常，用多边形顶点的序列来表示一个凸多边形，即P=<v0 ,v1 ,… ,vn-1>表示具有n条边v0v1，v1v2，… ,vn-1vn的一个凸多边形，其中，约定v0 = vn 。
若vi与vj是多边形上不相邻的两个顶点，则线段vivj称为多边形的一条弦。弦将多边形分割成凸的两个子多边形<vi ,vi+1 ,… ,vj>和<vj ,vj+1 ,… ,vi>。多边形的三角剖分是一个将多边形分割成互不重迭的三角形的弦的集合T。

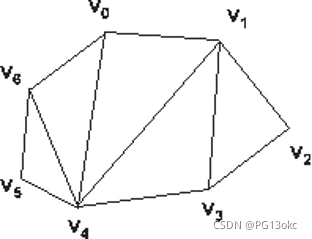
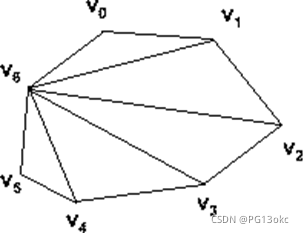
如上图为一个凸多边形的两个不同的三角剖分.n在凸多边形P的一个三角剖分T中，各弦互不相交且弦数已达到最大，即P的任一不在T中的弦必与T中某一弦相交。

有n个顶点的凸多边形的三角剖分中，恰好有n-3条弦和n-2个三角形。
凸多边形最优三角剖分的问题是：给定一个凸多边形P=<v0,v1,… ,vn-1>以及定义在由多边形的边和弦组成的三角形上的权函数ω。要求确定该凸多边形的一个三角剖分，使得该三角剖分对应的权即剖分中诸三角形上的权之和为最小!

可以定义三角形上各种各样的权函数W。例如：定义 ω(△vivjvk) = |vivj| + |vivk| + |vkvj|,其中，|vivj|是点vi到vj的欧氏距离。相应于此权函数的最优三角剖分即为最小弦长三角剖分。
注意：解决此问题的算法必须适用于任意的权函数。

二.解题思路

这是计算几何学问题，但在本质上与矩阵连乘积的最优计算次序问题极为相似。可用动态规划算法。

1. 三角剖分的结构及其相关问题

凸多边形的三角剖分与表达式的完全加括号方式之间具有十分紧密的联系。正如矩阵连乘积的最优计算次序问题等价于矩阵链的完全加括号方式.这些问题之间的相关性可从它们所对应的完全二叉树的同构性看出。所谓完全二叉树是指叶结点以外的所有结点的度数都为2的二叉树。

一个表达式的完全加括号方式对应于一棵完全二叉树，这棵二叉树叫作表达式的语法树。
例：与完全加括号的矩阵连乘积((A1(A2A3))(A4(A5A6)))对应的语法树如图(a)。

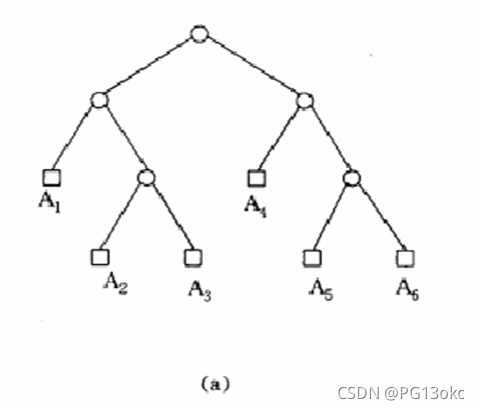
叶结点：表达式中一个原子。在语法树中，表达式(ELEr)对应一棵子树，其左子树表示表达式EL，其右子树表示表达式ER。有n个原子的完全加括号表达式与一棵有n个叶结点的语法树一一对应。

凸多边形<v0 ,v1 ,… ,vn-1>的三角剖分也可以用语法树来表示。例如，图3(a)中凸多边形的三角剖分可用图(b)所示的语法树来表示。该语法树的根结点为边v0v6，三角剖分中的弦组成其余的内部结点。

除v0v6以外的边是叶结点。树根v0v6是三角形v0v3v6的一条边，该三角形将原多边形分为3个部分：一个三角形，两个凸多边形.
三角形v0v3v6的另外两条边，即弦v3v6和v0v3为根的两个儿子。以它们为根的子树分别表示凸多边形<v0 ,v1 ,… ,v3>和凸多边形<v3 ,v4 ,… ,v6>的三角剖分

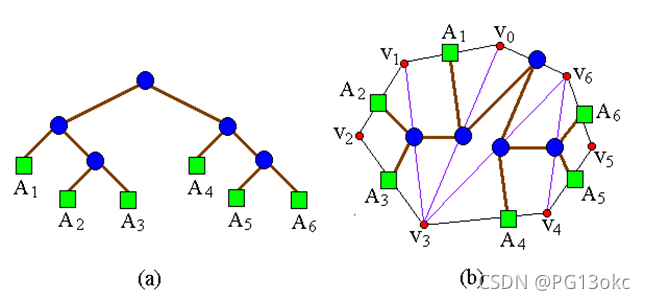
一个凸n边形的三角剖分与n-1个叶子的语法树一一对应。由于n个矩阵的完全加括号乘积与n个叶子的语法树之间存在一一对应关系，因此n个矩阵的完全加括号乘积也与凸(n+1)边形的三角剖分之间存在一一对应关系。上图中(a)和(b)表示出了这种对应关系，这时n=6。矩阵连乘积A1A2…A6中的每个矩阵Ai对应于凸(n+1)边形中的一条边vi-1vi。三角剖分中的一条弦vivj，i<j-1，对应于矩阵连乘积Ai+1…j 。

n矩阵连乘积的最优计算次序问题是凸多边形最优三角剖分问题的一个特殊情形。

对于给定的矩阵链A1A2…An，定义与之相应的凸(n+1)边形P=<v0 ,v1 ,… ,vn>，使得矩阵Ai与凸多边形的边vi-1vi一一对应。若矩阵Ai的维数为pi-1×pi , i=1,2,…,n，则定义三角形vivjvk上的权函数值为： ω(△vivjvk)=pipjpk。
依此权函数的定义，凸多边形P的最优三角剖分所对应的语法树给出矩阵链A1A2…An的最优完全加括号方式。

2.最优子结构性质

凸多边形的最优三角剖分问题有最优子结构性质。

若凸(n+1)边形P=<v0 ,v1 ,… ,vn>的一个最优三角剖分T包含三角形v0vkvn ， 1≤k≤n-1，则T的权为3个部分权的和，即三角形v0vkvn的权，子多边形<v0 ,v1 ,… ,vk>的权和<vk ,vk+1 ,… ,vn>的权之和。由T所确定的这两个子多边形的三角剖分也是最优的，因为若有<v0 ,v1 ,… ,vk>或<vk ,vk+1 ,… ,vn>的更小权的三角剖分，将会导致T不是最优三角剖分的矛盾。

3.最优三角剖分的递归结构

定义t[i,j]，1≤i<j≤n，为凸子多边形<vi-1 ,vi ,… ,vj>的最优三角剖分所对应的权值，即最优值。
设退化的多边形<Vi-1 ,vi>权值为0，那么凸(n+1)边形对应的权的最优值为t[1,n]。
t[i,j]的值可以利用最优子结构性质递归地计算。由于退化的2顶点多边形的权值为0，所以t[i,i]=0，i=1,2,…,n 。当j-i≥1时，子多边形<vi-1 ,vi ,… ,vj>至少有3个顶点。

由最优子结构性质,t[i,j]的值应为t[i,k]的值加上t[k+1,j]的值，再加上△vi-1vkvj的权值，并在i≤k≤j-1的范围内取最小。由此，t[i,j]可递归地定义为：

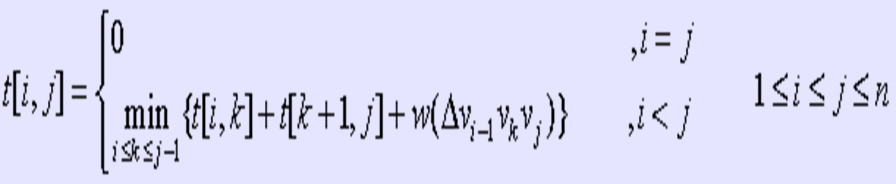
4.计算最优值

上式与矩阵连乘积的最优计算次序问题中计算m[i,j]的公式(P40)几乎完全一样（除了权函数的定义外），因此，对计算m[i,j]的算法Matrix_Chain略做修改就可用于计算t[i,j]。

计算凸(n+1)边形P=<v0 ,v1 ,… ,vn>的三角剖分最优权值的动态规划算法，输入是凸多边形P=<v0 ,v1 ,… ,vn>的权函数ω，输出是最优值t[i,j]和使得t[i,k]+t[k+1,j]+ω(△vi-1vkvj)达到最优的位置(k=)s[i,j]，1≤i≤j≤n 。

5.构造最优三角剖分

对于任意的1≤i≤j≤n ，上述算法在计算每一个子多边形<vi-1 ,vi ,… ,vj>的最优三角剖分所对应的权值t[i,j]的同时，还在s[i,j]中记录了此最优三角剖分中与边(或弦)vi-1vj构成的三角形的第三个顶点的位置。

因此，利用最优子结构性质并借助于s[i,j]，1≤i≤j≤n ，凸(n+l)边形P=<v0 ,v1 ,… ,vn>的最优三角剖分可容易地在Ο(n)时间内构造出来

代码如下:

// 凸多边形最优三角剖分
// 与矩阵连乘一样的思路。矩阵连乘的最优计算次序问题是凸多边形最优三角剖分问题的特殊情形
#include<bits/stdc++.h>
using namespace std;

const int N = 7; //凸多边形边数+1
int weight[][N] = {{0,2,2,3,1,4},{2,0,1,5,2,3},{2,1,0,2,1,4},{3,5,2,0,6,2},{1,2,1,6,0,1},{4,3,4,2,1,0}};//凸多边形的权
int  MinWeightTriangulation(int n, int **t, int **s);
void Traceback(int i, int j, int **s);  //构造最优解
int Weight(int a, int b, int c);    //权函数

int main()
{
    int **s = new int *[N];
    int **t = new int *[N];
    for(int i=0; i<N; i++)
    {
        s[i] = new int[N];
        t[i] = new int[N];
    }
    cout<<"此多边形的最有三角剖分值为："<<MinWeightTriangulation(N-1, t, s)<<endl;
    cout<<"最优三角剖分结构为："<<endl;
    Traceback(1, 5, s);//s[i][j]记录了Vi-1和Vj构成三角形的第三个顶点的位置
    system("pause");
    return 0;
}
int MinWeightTriangulation(int n, int **t, int **s)
{
    for(int i=1; i<=n; ++i) t[i][i] = 0;
    for(int r=2; r<=n; ++r)  //r表示凸子多边形的顶点数
        for(int i=1; i<=n-r+1; ++i)
        {
            int j = i+r-1;
            t[i][j] = t[i+1][j] + Weight(i-1, i, j);
            s[i][j] = i;
            for(int k=i+1; k<i+r-1; k++)
            {
                int u = t[i][k] + t[k+1][j] + Weight(i-1, k, j);
                if(u<t[i][j])
                {
                    t[i][j] = u;
                    s[i][j] = k;
                }
            }
        }
    return  t[1][N-2];
}
void Traceback(int i, int j, int **s)
{
    if(i==j) return;
    Traceback(i, s[i][j], s);
    Traceback(s[i][j]+1, j, s);
    cout<<"三角剖分顶点：V"<<i-1<<",V"<<j<<",V"<<s[i][j]<<endl;
}
int Weight(int a, int b, int c)
{
    return weight[a][b] + weight[b][c] + weight[a][c];
}

运行结果:

本篇文章参考我的老师毕方明《算法设计与分析》课件.
欢迎大家访问我的个人博客 — 乔治的编程小屋,和我一起为大厂offer努力吧!