递归分治 --- 例题5.线性时间选择

递归分治 — 例题5. 线性时间选择

---

一.问题描述

给定线性序列集中的n个元素和正整数k, 1≤ k≤ n, 求第k小元素的位置.

二.解题思路

该篇文章中我们讨论与排序问题类似的元素选择问题,元素选择问题的一般提法是:给定线性序集合中n个元素和一个整数k(1 <= k <= n),要求找出这n个元素中第k小的元素,即如果将这n个元素依其线性排列数时,排在第k个位置的元素即为要找的元素.

①最直观的解题方法:
先排序,然后找到第k小的元素即可.这样时间复杂度至少是: O(n), 平均: O(nlogn)时间

②随机选择算法:
模仿快速排序对输入数组A进行二分划分,使子数组A1的元素<=A2中的元素,分点J由随机数产生,若K<=J,则K为A1的第K小元, 若K>J,则K为A2的第K-J小元.
与快速排序算法不同,它只对子数组之一进行递归处理。

按照上面的思路,我们先用上篇文章说到过的随机选择算法来确定基准,从而对数组进行划分.

代码描述:

template<class T>
int randomizedPartition(vector<T> &a, int p, int r)  //在p:r中随机选择一个数i
{
    srand(int(time(0)));  //每次以当前时间作为随机数生成的种子
    int i = random(p, r);
    swap(a[i], a[p]);  //将a[i]换到左端点
    return Partition(a, p, r);
}
Type RandomizedSelect(Type a[], int p, int r, int k)
{
	if(p == r) return a[p];
	int i = RandumizePartition(a, p, r);	//使用了快速排序那篇文章中的RandomziedPartition随机划分算法
	j = i-p+1;  //j为a[p:i]中的元素个数
	if(k <= j)
		return RandomizedSelect(a, p, i, k);
	else
		return RandomizedSelect(a, i+1, r, k-j);
}

时间复杂度分析:

• 若分点总是等分点,则有: Tmin(n) = d

  ​ Tmin(n) = T(n/2) + cn, 计算得到T(n) = θ(n)

• 若一部分总是为空,则有: Tmax(n) = O(n^2)

从上面可以看到,我们若果使用随机划分的话,最坏情况下,算法RandomizedSelect时间复杂度达到了O(n^2),例如,我们在找最小元素时,总是在最大元素处划分.尽管如此,该算法的性能还是可以的.
随机选择算法的最佳情况即线性选择!!!

③线性时间选择算法(证明比较绕,可以直接记住结论:每次选择的基准为中位数的中位数,这样可以保证我们每次递归划分问题规模缩小1/4.当元素个数小于阈值的话,我们直接用sort排序)

我们可以通过寻找一个好的划分基数,可使最坏情况下时间为O(n).

下面我们来介绍一下如何划分可以达到目标,具体步骤如下:

可以按以下步骤找到满足要求的划分基准,(「」表示向下取整,符号打不出来见谅.)

• 将n个输入元素划分成「n/5」个组，每组5个元素，除可能有一个组不是5个元素外。用任意一种排序算法，将每组中的元素排好序，并取出每组的中位数，共「n/5」个。
• 递归调用Select找出这「n/5」个元素的中位数。如果「n/5」是偶数，就找它的两个中位数中较大的一个。然后以这个元素作为划分基准

下图是上述划分策略的示意图，其中n个元素用小圆点来表示，空心小圆点为每组元素的中位数。中位数的中位数x在图中标出。图中所画箭头是由较大元素指向较小元素的。

如下图所示:

为了简化问题,我们先设所有元素互不相同.在这种情况下,找出的基准x至少比3「(n-5)/10」个元素大,因为在每组中有两个元素小于本组的中位数,而「n/5」个中位数中又有「(n-5)/10」个小于基准x.同理可得基准x至少比3「(n-5)/10」个元素小.

图中红色框起来的就是必然小于基准的元素,蓝色框起来的就是必然大于基准的元素.
而当n>=75时,3「(n-5)/10」 >= n/4.所以,按照此基准划分所得的两个子数组的长度都至少缩短1/4,这一点是至关重要的.
下面,据此我们来计算一下时间复杂度.

设对n个元素的数组调用Select需要T(n)时间,那么找中位数的中位数x至多用T(n/5)的时间.现已证明,按照算法所选的基准x进行划分所得到的两个子数组分别至多由3n/4个元素,所以无论对哪一个子数组进行调用Select都至多需要T(3n/4)时间.(这就是为什么要选择中位数的中位数为基准)
故可得到关于T(n)的递归式:

• T(n) <= C1 , n<75
• T(n) <= C2n + T(n/5) + T(3n/4), n>=75

解此递归式可得到:T(n) = O(n)

代码如下:

#include<bits/stdc++.h>
using namespace std;
const int N = 1e8+10;
int p[N];
int Partition(int a[], int low, int high, int x)
{
    int key = x;
    while(low<high)
    {
        while(low<high&&a[high]>key) --high;
        a[low] = a[high];
        while(low<high&&a[low]<=key) ++low;
        a[high] = a[low];
    }
    a[low] = key;
    return low;
}
// 线性时间选择
int select(int a[], int  left, int right, int k)  //找出第k小的数
{
    if(right-left<75)  //元素个数小于阈值,直接sort排序
    {
        sort(a, a+right-left+1);  //如果元素个数不够多,选择简单排序算法排序
        return a[left+k-1];
    }
    for(int i=0; i<=(right-left-4)/5; ++i)   //(right-left-4)/5表示分成多少组,即有多少个中位数,即(n-5)/5
    {
        sort(a+left+5*i, a+left+5*i+4); //每五个元素一组,分别排序
        swap(a[left+i*5+2], a[left+i]); //将每一组的中位数调到整个数组最前面
    }
    int x = select(a, left, left+(right-left-4)/5, (right-left-4)/10); //x为中位数的中位数
    int loc = Partition(a, left, right, x), j = loc-left+1;  //j表示一半数组的元素个数
    if(k <= j) return select(a, left, loc, k);  //针对所有元素互不相等的情况,如果有元素相等的话,需要再加操作.
    else  return select(a, loc+1, right, k-j);
}
int main()
{
    cout<<"线性时间选择"<<endl;
    int n, k;
    cout<<"请输入数组大小以及要查找第几小的元素:";
    while(cin>>n>>k && n)
    {
        memset(p, 0, sizeof(p));
        cout<<"请输入数组元素:";
        for(int i=0; i<n; ++i)
            scanf("%d", &p[i]);
        printf("%d\n", select(p, 0, n-1, k));
        cout<<"请输入数组大小以及要查找第几小的元素:";
    }  
    
    
    // // 做一个测试:
    // // srand(time(0));  //随机数生成的种子
    // for(int i=0; i<1000000; ++i)
    // {
    //     p[i] = rand()%1000000;
    // }
    // cout<<"数据量:1000000"<<endl;
    // clock_t start, end;
    // clock_t start2, end2;
    // start = clock();
    // int ans = select(p, 0, 999999, 1324);
    // for(int i=0; i<1326; i++) cout<<p[i]<<" ";
    // cout<<"第1324小的个数据为:"<<ans<<endl;
    // end = clock();
    // cout<<"线性时间选择算法用时: "<<double(end-start)/CLOCKS_PER_SEC<<endl;
    // start2 =  clock();
    // sort(p, p+999999);
    // cout<<"第1324个小的数据为:"<<p[1324]<<endl;
    // for(int i=0; i<1326; i++) cout<<p[i]<<" ";
    // end2 = clock();
    // cout<<"快速排序选择算法用时: "<<double(end2-start2)/CLOCKS_PER_SEC<<endl;
    system("pause");
    return 0;
}

运行结果:

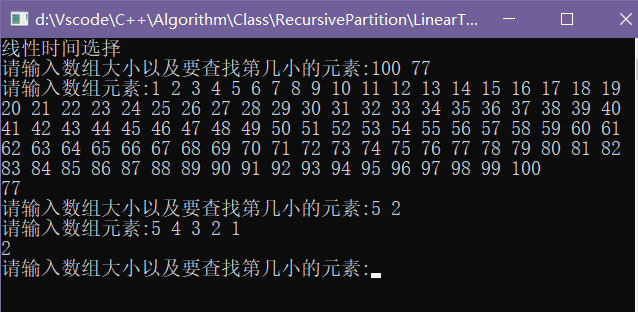
我还做了一个小小的对比,观测两种算法的效率相差如何:

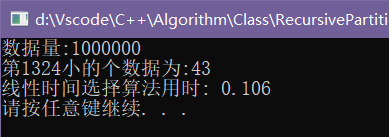
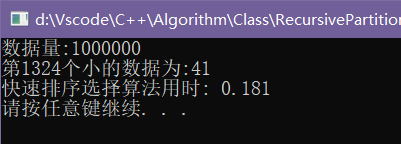
可以看到,当数据量为1000000时,效率差距已经逐渐显现出来了,到了更大的计算量的话,一个好的算法确实是能够节省很多资源.

算法优化过程:

算法	快排	随机选择	线性时间选择
时间复杂度	O(nlogn)	O(n)-O(n^2)	O(n)
基准值	a[p]	random(p,r)	中位数

欢迎大家访问我的个人博客乔治的编程小屋,和我一起体验一下养成式程序员的打怪升级之旅吧!