–记录自己学习的步伐,点滴的生活,以后学习和复习使用。纯手打,代码不抄袭。–

来源百度百科,具体定义和性质可以查看百度百科的内容。马尔科夫链
或者看一下下面的这个文章,也是翻译转载过来的。偷渡一下:[译] 用 Python 实现马尔可夫链的初级教程
用概率数学公式表示如下:
Pr( Xn+1 = x | X1 = x1, X2 = x2, …, Xn = xn) = Pr( Xn+1 = x | Xn = xn)
就是说 Xn+1 的概率只和之前的 Xn 的概率有关。所以只需要知道上一个状态就可以确定现在状态的概率分布,满足条件独立(也就是说:只需要知道现在状态就可以确定下一个状态,而之前的所有状态,都不会影响)。
例1:
某计算机机房的一台计算机经常出现故障,研究者每隔15分钟观察一次计算机的运行状态,手机了24小时的数据,用1表示正常,0表示不正常。数据如下:
str1 =
"1110010011111110011110111111001111111110001101101111011011010111101110111101111110011011111100111"
假定这就是无规律,白噪声的序列,我也没有做过白噪声检验,反正就用这个例子做了。
现在有四种情况,分别是:
第一步1之后出现下一步0,表示为10
第一步1之后出现1,表示为11
0之后出现0,表示为00
0之后出现1,表示为01
那么要预测下一个时间点将会出现的状态。
首先要计算上面4中情况一共出现多少次,然后才能计算概率。
比如111,里面出现11的情况有两次,而不是一次。这就要做循环统计了。
统计出每一个多少,然后做转移矩阵。样式跟下面这个类似
| 0 | 1 | |
|---|---|---|
| 0 | … | … |
| 1 | … | … |
其中index上面的0表示当前的一步,就第一步,columns上面的0表示下一步。也不是绝对的要这种形式,只要自己看得懂就行,自己有个习惯,并记住也能让别人看懂就好。
# 计算ab在s中出现的次数
def find_count(s,ab):
ab_sum = 0
for i in range(0,len(s)-1):
if s[i:i+2] == ab:ab_sum+=1
return ab_sum
# 转移矩阵
def str_count_df(s):
# 获得里面不重复的元素
unique_items = np.unique(list(s))
# 获得不重复元素个数
n = unique_items.size
# 默认行是这一次的,列是下一次的。类容是他们的转换情况
df_ = pd.DataFrame(index=unique_items,columns=unique_items)
for i in unique_items:
for j in unique_items:
df_.loc[i,j] = find_count(s,i+j)
return df_
# 转移矩阵,概率
def str_count_df_p(s):
# 获得里面不重复的元素
unique_items = np.unique(list(s))
# 获得不重复元素个数
n = unique_items.size
# 默认行是这一次的,列是下一次的。类容是他们的转换情况
df_ = pd.DataFrame(index=unique_items,columns=unique_items)
for i in unique_items:
for j in unique_items:
df_.loc[i,j] = find_count(s,i+j)
df_ = df_.div(df_.sum(axis=1),axis='index')
return df_
上面两个转移矩阵代码是一样的,只不过最后返回值不一样,一个是转换成概率了,一个没转。
用上面的函数,将str1带进去就会得到转移矩阵

表示0→1共发生18次,以此类推…
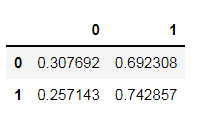
表示如果当前是0,那么下一个是0的概率为30.77%,下一步为1的概率为69.23%。
每一行的和是1.这好理解的。
对当前数据,最后一个为1,那么预测下一步,有74.3%的概率不发生故障。
上面的方法不仅仅局限于两个类别的0和1,任何类别的转换都可以。
比如下面的观测系统数据:
str2 = "4321431123212344331113321222442323112431"
带入也可直接得到转移矩阵
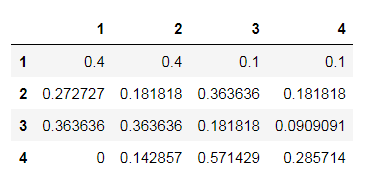
这计算的都是一步转移概率矩阵。
如果是两步转移矩阵,就是一步转移矩阵的二次方。三步转移矩阵就是三次方,n步就是n次方
这是数学上已经证明过的。
现在我们假设下一步出现1,2,3,4的概率为 [0.1,0.3,0.2,0.4]
那么第二步出现的概率就可以算出来,用第一次的乘以转移矩阵:
#上面的转移矩阵为 df_2
np.array([0.1,0.3,0.2,0.4]).dot(np.array(df_2,dtype=np.float64))
out:
array([0.19454545, 0.22441558, 0.38402597, 0.19701299])
那么第三步:就是第一步*df_2的二次方,以此类推。
当n趋于无穷,最终的结果会不变。
# 这是第四步
np.array([0.1,0.3,0.2,0.4]).dot(
np.linalg.matrix_power(np.array(df_2,dtype=np.float64),3)
)
out:
array([0.29265661, 0.28825609, 0.27010259, 0.14898471])
# 这是第10步
np.array([0.1,0.3,0.2,0.4]).dot(
np.linalg.matrix_power(np.array(df_2,dtype=np.float64),9)
)
out:
array([0.29393371, 0.28893058, 0.26829268, 0.14884303])
# 这是第20步
np.array([0.1,0.3,0.2,0.4]).dot(
np.linalg.matrix_power(np.array(df_2,dtype=np.float64),19)
)
out:
array([0.29393371, 0.28893058, 0.26829268, 0.14884303])
通过上面可以看出,最后已经不再变化。
不管你一开始的概率,也就是第一步的概率是多少,最后都会是这个结局。
跟第一步没关系。
这就是这个转移矩阵的极限分布。
这个在市场分析,或者市场占有率上,很有用。最后趋于一个恒定值,就是拥有多大的市场份额。
(假如这1,2,3,4分别代表不同的商品的话)
另外这个极限值是可以求出来的。我们假设它为(p1,p2,p3,p4)
可以知道这个向量,乘以转移矩阵以后还是它这个向量本身,所以不管它乘以多少个转移矩阵,都不会变化。
假如转移矩阵为:
[[a1,a2,a3,a4]
[b1,b2,b3,b4]
[c1,c2,c3,c4]
[d1,d2,d3,d4]]
根据矩阵乘积运算。有:
p1 X a1+p2Xb1+p3Xc1+p4Xd1=p1
p1 X a2+p2Xb2+p3Xc2+p4Xd2=p2
p1 X a3+p2Xb3+p3Xc3+p4Xd3=p3
p1 X a4+p2Xb4+p3Xc4+p4Xd4=p4
就是1 * 4的矩阵乘以4 * 4的矩阵。等于1 * 4的矩阵。
并且p1+p2+p3+p4=1
通过这5个方程就可以求出来p1,p2,p3,p4
用Python计算的时候,如果用scipy.linalg里面的solve,会有问题,因为这个方法要求传入的是一个方阵,可是这里有五个方程,四个未知数,无法求出。
我试过很多次,都不行,但可以去掉一个方程求得近似解。
我也是找了很久,有这么一个方法可以求:
# Return the least-squares solution to a linear matrix equation.
# 用最小二乘法来求解,a是系数矩阵,b是结果
np.linalg.lstsq(a,b)
代码:
# 注意看上面的方程,原转移矩阵要转置,并减去一个单位阵。
a = np.array(df_2,dtype=np.float64).T
a = a-np.eye(4)
a = np.append(a,np.array([1,1,1,1])).reshape(-1,4)
np.linalg.lstsq(a,np.array([0,0,0,0,1]))
out:
# 第一个返回值为我们要求得p1到p4
(array([0.29393371, 0.28893058, 0.26829268, 0.14884303]),
array([1.02992113e-33]),
4,
array([2.01437748, 1.25270383, 1.05972215, 0.70596599]))
# 第二个返回值为残差。第三个返回值时秩,第四个为矩阵奇异值
并不是每一个转移矩阵n次方后都会平稳趋于一个定矩阵,这个平稳等性质,可以搜别的文章,有的不趋于,有的单数次趋于一个偶数次趋于一次。等等。
如果对一个转移概率矩阵进行n次方,他得到的值越来越小,但是每个值占的百分比却一直不变,那有可能是数值的精度问题,碰到过,后来转成分数就好了。或者求一下极限分布。
下面看一个有意思的问题,我也是在知乎上看到的。
不过他只给出了四个格子的步骤和方法。
如下图所示的迷宫共有9个格子,相邻格子有门相通,9号格子就是迷宫出口.
整个迷宫将会在5分钟后坍塌. 1号格子有一只老鼠,这只老鼠以每分钟一格的速度在迷宫里乱窜(它通过各扇门的机会均等)。
求此老鼠在迷宫坍塌之前逃生的概率。如果这只老鼠速度提高一倍,则老鼠在迷宫坍塌之前逃生的概率能增加多少?

以上是2018年上海应用数学知识竞赛的一道初赛试题。
对于这个问题,先求出他的转移概率矩阵,那么一切就好办了。
9 * 9的矩阵,而且从1到2和3的概率相同,其他也一样。如下:
# 写出每个格子的转移矩阵
a = np.array([
[0,0.5,0,0.5,0,0,0,0,0],
[1/3,0,1/3,0,1/3,0,0,0,0],
[0,0.5,0,0,0,0.5,0,0,0],
[1/3,0,0,0,1/3,0,1/3,0,0],
[0,0.25,0,0.25,0,0.25,0,0.25,0],
[0,0,1/3,0,1/3,0,0,0,1/3],
[0,0,0,0.5,0,0,0,0.5,0],
[0,0,0,0,1/3,0,1/3,0,1/3],
[0,0,0,0,0,0,0,0,1]
])
由于第一步在1的位置,所以第一步走下去的概率为:
f = np.array([0,0.5,0,0.5,0,0,0,0,0])
那么计算5步的时候概率:
f.dot(np.linalg.matrix_power(a,4))
out:
array([0. , 0.27777778, 0. , 0.27777778, 0. ,0.16666667, 0., 0.16666667, 0.11111111])
所以停在9的概率也就是出去的概率为0.111111111
速度加快就是一分钟走两步,五分钟10步。
f.dot(np.linalg.matrix_power(a,9))
array([0.1399177 , 0. , 0.11316872, 0. , 0.22633745,
0. , 0.11316872, 0. , 0.40740741])
假定时间趋于很大的时候,求它的极限分布:
(代码不重复写了。根据那个公式构造)
array([ 1.42076747e-17, -5.55111512e-17, -1.66533454e-16, -8.67361738e-17,
-3.33066907e-16, -1.24900090e-16, -1.11022302e-16, -6.93889390e-17,
1.00000000e+00])
可以看得出来,最后9的概率等于1,其他的等于0.所以最终停留的地方一定是9,也就是出口。
继续,
倘若迷宫不存在出口,并且每个门通过概率一样。那么他最终停在每个格子上的概率是不是相同的?
重新构造他的转移概率矩阵:(其实就是最后一个行有变化,其他都一样)
a = np.array([
[0,0.5,0,0.5,0,0,0,0,0],
[1/3,0,1/3,0,1/3,0,0,0,0],
[0,0.5,0,0,0,0.5,0,0,0],
[1/3,0,0,0,1/3,0,1/3,0,0],
[0,0.25,0,0.25,0,0.25,0,0.25,0],
[0,0,1/3,0,1/3,0,0,0,1/3],
[0,0,0,0.5,0,0,0,0.5,0],
[0,0,0,0,1/3,0,1/3,0,1/3],
[0,0,0,0,0,0.5,0,0.5,0]
])
求第103步和104步的概率分布情况
f = np.array([0,0.5,0,0.5,0,0,0,0,0])
print(f.dot(np.linalg.matrix_power(a,102)))
print(f.dot(np.linalg.matrix_power(a,103)))
out:
[0,0.25,0.,0.25,0, 0.25,0,0.25,0]
[0.16666667,0. , 0.16666667 ,0. , 0.33333333 0.
0.16666667 ,0. ,0.16666667]
多算几个你就会发现他是上面两组的交替,也就是奇数、偶数次会有不同的结果。
我们用上面公式求得他的极限分布p1-p9:
a_ = a.T-np.eye(9)
a_ = np.append(a_,np.array([1,1,1,1,1,1,1,1,1])).reshape(-1,9)
np.linalg.lstsq(a_,np.array([0,0,0,0,0,0,0,0,0,1]))
array([0.08333333, 0.125 , 0.08333333, 0.125 , 0.16666667,
0.125 , 0.08333333, 0.125 , 0.08333333])
结果其实就是上面交替的两个矩阵的平均值。这就是他们最终每个点停靠的概率。





















 3039
3039











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








