表达式树

最新推荐文章于 2024-07-30 20:25:46 发布

tomjourney

最新推荐文章于 2024-07-30 20:25:46 发布

阅读量1.2k

点赞数

分类专栏： (1)dataStructure&Alg 文章标签：表达式树数据结构

本文链接：https://blog.csdn.net/PacosonSWJTU/article/details/49308969

版权

(1)dataStructure&Alg 专栏收录该内容

74 篇文章 4 订阅

订阅专栏

【0】README

0.1）本文旨在总结出表达式树的构建步骤，其中还涉及到中缀转后缀表达式，以及如何计算表达式树中的值；
0.2）本文源代码均为原创；
0.3） 其实，实现一个简单的计算器，也即求出中缀表达式的值，我们也可以用栈来实现，参见 http://blog.csdn.net/pacosonswjtu/article/details/49225529 ；此处给出表达式树的实现仅在于加深对表达式树的理解及它的应用；

【1】表达式树的相关概念

1.1）定义：表达式树的树叶是操作数operand，比如常量或变量，而其他节点是操作符 operator；
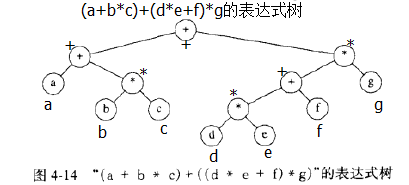
这里写图片描述
1.2）对上图中的表达式进行遍历（先序+中序+后序）

先序遍历： + + a * b c * + * d e f g
中序遍历： a + b * c + （ d * c + f ） * g （这里要加上括号，这也是我们为什么要采用后缀或逆波兰记法来表示用户输入的运算表达式以计算结果，一句话，方便可靠）
后序遍历： a b c * + d e * f + g * +
Attention）这里，我们没有给出源代码，因为这个先序，后序 or 中序的源代码和二叉树遍历的源代码相差无几，这里只是了解下表达式树的概念，并了解下用树的遍历计算表达式的值；

【2】如何构造一颗表达式树（表达式树的定义很关键，对于写我们的递归程序而言）

我们给出一种算法将后缀表达式转变为表达式树：

step1）用户输入中缀表达式，我们首先将其转为后缀表达式；
step2）我们将后缀表达式转为表达式树的形式；
step3）我们来计算该表达式树的计算结果是多少？

2.1 ) download source code: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter4/p71_compute_expr_tree

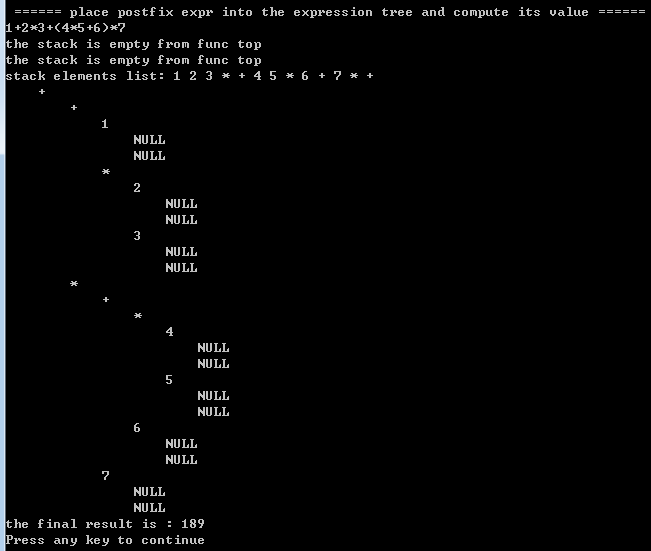
这里写图片描述
2.2 ) source code at a glance:

2.2.1）expr_tree.c source code :

#include "stack.h"
#include "binary_tree.h"

extern void infir_to_postfix();
extern int computeResult(int operand1, int operand2, int operator_);
extern ElementType compute_postfix();
extern Stack operand;
extern int isOperator(char ch);
extern int computeResult(int operand1, int operand2, int operator_);

// building an expr tree for storing postfix expr
BinaryTree postfixToExprTree()
{           
    int value;      
    BinaryTree* treeArray;  
    int size;
    int index;
    ElementType *p;
    int i ;

    size = getTopOfStack(operand) + 1; //get the top of stack, and add 1 to compute size of the stack
    treeArray = (BinaryTree*)malloc(size * sizeof(BinaryTree)); // alloc memory for treeArray
    index = 0; // set the index of treeArray 0 

    p = getArray(operand);
    i = 0;
    while(i < getTopOfStack(operand))
    {
        value = *(p+i++);
        if(value == ' ') // if the value equals ' ', continue 
            continue;
        treeArray[index++] = createBinaryTree(value);// for every element need to build tree node
        if(isOperator(value)) // if the value belongs to operator, 
        {   
            index--;                        
            insertNode(treeArray[index-1], treeArray[index], 0);            
            insertNode(treeArray[index-2], treeArray[index], 1);
            treeArray[index-2] = treeArray[index];
            index --;
        }       
        // (treeArray+index++) = createBinaryTree(value);// if the value belongs to operand, push the element into the treeArray
    }
    return *treeArray;
}

// preorder the tree
void printPreorder(int depth, BinaryTree root)
{           
    int i;

    if(root) {      
        for(i = 0; i < depth; i++)
            printf("    ");     
        printf("%c\n", root->value);
        printPreorder(depth + 1, root->left);                                           
        printPreorder(depth + 1, root->right); // Attention: there's difference between traversing binary tree and common tree                          
    }
    else {
        for(i = 0; i < depth; i++)
            printf("    ");     
        printf("NULL\n");
    }
}

// postordering expression tree with operantors and operands to compute the result of these nodes
int postorder_compute_postfix_expr_tree(BinaryTree root)
{   
    int temp1;
    int temp2;

    if(isOperator(root->value)) {                       
        temp1 = postorder_compute_postfix_expr_tree(root->left);                                            
        temp2 = postorder_compute_postfix_expr_tree(root->right); // Attention: there's difference between traversing binary tree and common tree                                       
        return computeResult(temp1, temp2, root->value);
    }
    else  
        return root->value - 48;     
}


int main()
{       
    BinaryTree bt;

    // 1.convert infix into postfix expr
    printf("\n ====== convert infix into postfix expr ====== \n");
    infir_to_postfix(); // after this func is called over, we get the postfix of the expr

    // 2.convert postfix into the expression tree   
    bt = postfixToExprTree();
    printPreorder(1, bt); 

    //3.compute postfix expr stored in the expression tree
    printf("the final result is : %2d \n", postorder_compute_postfix_expr_tree(bt));

    return 0;
}

2.2.2）binary_tree.c source code :

#include "binary_tree.h"

// create a BinaryTree with root node
BinaryTree createBinaryTree(TreeElementType value)
{   
    BinaryTree t;

    t = (BinaryTree)malloc(sizeof(struct BinaryTree));
    if(!t) {
        Error("out of space, from func createBinaryTree");        
        return NULL;
    }    
    t->left = NULL;
    t->right = NULL;    
    t->value = value;

    return t;
}

// make the BinaryTree empty 
BinaryTree makeTreeEmpty(BinaryTree t)
{
    if(t){
        makeTreeEmpty(t->left);
        makeTreeEmpty(t->right);        
        free(t);
    }           
    return NULL;
}

//insert a Tree node with value e into left child or right child of the parent
BinaryTree insert(TreeElementType e, BinaryTree parent, int isLeft)
{   
    BinaryTree node;

    if(!parent){
        Error("for parent BinaryTree node is empty , you cannot insert one into the parent node, from func insert");        
        return NULL;
    }

    node = (BinaryTree)malloc(sizeof(struct BinaryTree));
    if(!node) {
        Error("out of space, from func insert");        
        return NULL;
    }
    node->value = e;
    node->right = NULL;
    node->left = NULL;// building the node with value e over

    if(isLeft) { // the tree node inserting into left child of the parent 
        if(parent->left) {
            Error("for parent has already had a left child , you cannot insert one into the left child, from func insert");        
            return NULL;    
        }
        parent->left = node;
    }
    else { // the tree node inserting into right child of the parent 
        if(parent->right) {
            Error("for parent has already had a right child , you cannot insert one into the right child, from func insert");        
            return NULL;    
        }
        parent->right = node;
    }    
    return node;    
}

//insert a Tree node into left child or right child of the parent
BinaryTree insertNode(BinaryTree node, BinaryTree parent, int isLeft)
{           
    if(!parent){
        Error("for parent BinaryTree node is empty , you cannot insert one into the parent node, from func insert");        
        return NULL;
    }

    if(!node) {
        Error("for the node inserted is NULL , so you cannot insert a NULL node, from func insert");        
        return NULL;
    }    

    if(isLeft)  // the tree node inserting into left child of the parent        
        parent->left = node;     
    else  // the tree node inserting into right child of the parent         
        parent->right = node;        

    return node;    
}

// find the BinaryTree root node with value equaling to e
BinaryTree find(TreeElementType e, BinaryTree root)
{
    BinaryTree temp;

    if(root == NULL)
        return NULL;
    if(root->value == e)
        return root;

    temp = find(e, root->left); 
    if(temp) 
        return temp;
    else
        return  find(e, root->right);               
}

// analog print directories and files name in the BinaryTree, which involves postorder traversal. 
void printPostorder(int depth, BinaryTree root)
{           
    int i;

    if(root) {                      
        printPostorder(depth + 1, root->left);                                          
        printPostorder(depth + 1, root->right); // Attention: there's difference between traversing binary tree and common tree
        for(i = 0; i < depth; i++)
            printf("    ");     
        printf("%c\n", root->value);                    
    }
    else {
        for(i = 0; i < depth; i++)
            printf("    ");     
        printf("NULL\n");
    }
}

2.2.3）stack.h source code :

#include <stdio.h>
#include <malloc.h>

#define ElementType int
#define EmptyStack -1
#define Error(str) printf("%s",str) 
#define FatalError(str) printf("%s",str) 
#define minStackSize 5

struct Stack;
typedef struct Stack *Stack;

int isFull(Stack s);
int isEmpty(Stack s);
Stack createStack(int);
void disposeStack(Stack s);
void makeEmpty(Stack s);
void push(ElementType e, Stack s);
ElementType top(Stack s);
void pop(Stack s);
ElementType top(Stack s);
int getTopOfStack(Stack s);
ElementType *getArray(Stack s);

void printStack(Stack s); 
void printStack_postfix(Stack s);

struct Stack {
    int capacity;
    int topOfStack;
    ElementType *array;
} ;

2.2.4）binary_tree.h source code :

#include <stdio.h>
#include <malloc.h>

#define TreeElementType char
#define Error(str) printf("%s",str) 

struct BinaryTree;
typedef struct BinaryTree *BinaryTree;

BinaryTree createBinaryTree(TreeElementType); // this func is different from that in p70_preorder_binary_tree.c
BinaryTree makeTreeEmpty(BinaryTree);
BinaryTree insert(TreeElementType, BinaryTree, int);
BinaryTree insertNode(BinaryTree, BinaryTree, int);
BinaryTree find(TreeElementType, BinaryTree);
void printPostorder(int depth, BinaryTree root);

// we adopt child-sibling notation
struct BinaryTree
{
    TreeElementType value;
    BinaryTree left;
    BinaryTree right;
};

2.2.5）stack.c source code :

#include "stack.h"

int getTopOfStack(Stack s)
{
    return s->topOfStack;
}

//return stack's array
ElementType *getArray(Stack s)
{
    return s->array;
}

//judge whether the stack is empty or not
int isFull(Stack s)
{
    return s->capacity - 1 == s->topOfStack ? 1 : 0;    
}

//judge whether the stack is empty or not
int isEmpty(Stack s)
{
    return s->topOfStack == -1;
}

//create stack with the head node 
Stack createStack(int size)
{
    Stack s;

    s = (Stack)malloc(sizeof(struct Stack));

    if(size < minStackSize) {
        Error("stack size is too small, and creating stack with defualt size 5");   
        size = minStackSize;
    }
    if(s == NULL) {
        FatalError("out of space when allocting memory for stack s");
        return NULL;
    }

    s->array = (ElementType *)malloc(size * sizeof(ElementType));   
    if(s->array == NULL) {
        FatalError("out of space when allocting memory for stack's array ");
        return NULL;
    }
    s->topOfStack = -1;
    s->capacity = size; 
    return s;
}

//dispose stack 
void disposeStack(Stack s)
{
    free(s->array);
    free(s);
}

//pop all elements in the stack
void makeEmpty(Stack s)
{
    if(s->topOfStack == -1)
        Error("must create the stack first");
    while(!isEmpty(s))
        pop(s);
}

//push the node with value e into the stack s 
//attend that first moving ptr ,then executing push operation
void push(ElementType e, Stack s)
{
    ElementType *temp = s->array;

    if(isFull(s))
        Error("the Stack is full, push failure! ");         
    else{
        s->topOfStack ++;
        s->array[s->topOfStack] = e;                
    }       
}

// pop the node or element on the top of stack 
//attend that first executing pop operation,then moving ptr
void pop(Stack s)
{

    if(isEmpty(s))
        Error("empty stack");
    else 
        s->topOfStack --;                            
}

// return the value of the top node in the stack
ElementType top(Stack s)
{
    if(!isEmpty(s))     
        return s->array[s->topOfStack];
    Error("the stack is empty from func top\n");
    return -1;
}

//print value of element in the stack s
void printStack(Stack s)
{
    int i;

    if(isEmpty(s)){
        Error("empty stack");
        return ;
    }

    for(i=0; i<= s->topOfStack; i++) 
        printf("%4d", s->array[i]);

    printf("\n");
}

//print value of element in the stack s with postfix
void printStack_postfix(Stack s)
{
    int i;

    if(isEmpty(s)){
        Error("empty stack");
        return ;
    }
    printf("stack elements list: ");
    for(i=0; i<= s->topOfStack; i++)    
        printf("%c", s->array[i]);

    printf("\n");
}

2.2.6）compute_postfix.c source code :

#include "stack.h"

#define Size 100

// refer to p50.c and put it into the same project
extern struct Stack;
typedef struct Stack *Stack;

extern Stack operand; // operand is an extern variable defined in infixToPostfix 
extern int isOperator(char ch);
extern void infir_to_postfix();
int computeResult(int operand1, int operand2, int operator_);

int computeResult(int operand1, int operand2, int operator_)
{
    switch(operator_)
    {
    case '+': return operand1 + operand2;
    case '*': return operand1 * operand2;
    default: return 0; break;
    }
}

// compute final result of responding postfix 
ElementType compute_postfix()
{
    Stack output;
    int i;
    ElementType *p;
    int value;
    int operand1;
    int operand2;

    output = createStack(Size); // create stack with length Size
    i = 0;
    p = getArray(operand); // get operand->array

    while(i < getTopOfStack(operand))
    {
        value = *(p+i++);
        if(value == ' ')
            continue;
        if(isOperator(value))
        {
            operand1 = top(output);
            pop(output);

            operand2 = top(output);
            pop(output);

            value = computeResult(operand1, operand2, value);
            push(value, output);
            continue;
        }
        push(value - 48, output);
    }
    return getArray(output)[0];
}

2.2.7）infixToPostfix.c source code :

#include "stack.h"

#define Size 100

// refer to p50.c and put it into the same project
extern struct Stack;
typedef struct Stack *Stack;
Stack operand; // declaration of Stack operand 
int isOperator(char ch);
void infir_to_postfix();

//compare operator's priority between ch1 and ch2, return -1, 0 or 1 
int priorityBigger(char ch1, char ch2)
{
    int size = 8;
    char operator_[]={ '(', ')', ' ', '+', '-', ' ', '*', '/'};
    int index1, index2;
    int i;

    if(ch1 - ch2 == 0)
        return 0;

    for(i = 0; i< size; i++)
        if(operator_[i] == ch1)
            index1 = i;          
        else if(operator_[i] == ch2)
            index2 = i;                  

    index1 -= index2;

    if(index1 == 1 || index1 == -1) 
        return 0;
    else if(index1 > 1)
        return 1;
    else if(index1 < -1)
        return -1;  
}


//judge whether the ch is operator or not ,also 1 or 0
int isOperator(char ch)
{
    int size;
    char operator_[]={'(', '+', '-', '*', '/', ')'};
    int i;

    size = 6;
    for(i = 0; i < size; i++)
        if(ch == operator_[i])
            break;

    return i == size ? 0 : 1;
}

//convert a part of str with length len into responding element value 
ElementType strToElement(int *str, int len)
{
    int i;
    int value;

    i = value = 0;
    while(i < len)
    {
        value += *(str+i) - 48;
        if(++i == len)
            break;
        value *= 10;
    }
    return value;
}

// convert infix expr into postfix expr
//for operand and operator cannot be in the same type ,we treat them as char and split them with space
void infixToPostfix(Stack s1, Stack s2,char *expr)
{
    char ch;    
    int i;
    char top_t; 
    int flag;       

    i = 0;  
    flag = 0;    
    while((ch = *(expr+i++)) != '\0') 
    {               
        if(ch == ')'){// if ch equals ')', pop elements in stack s2 between '(' and ')' into stack s1
            while((top_t = top(s2)) != '(' ) 
            {           
                push(top_t, s1);
                push(' ', s1);
                pop(s2);
            }           
            pop(s2); // pop '(' in stack s2             
            continue;
        }

        if(isOperator(ch)) // isOperator is true                    
        { 
            if(ch == '(') 
            {
                push(ch, s2); // push '(' into operator stack s2
                flag = 1;
                continue;
            }           

            while((top_t = top(s2)) != -1 && priorityBigger(top_t, ch) >= 0 && flag ==0) 
            {                           
                pop(s2);                 
                push(top_t, s1);
                push(' ', s1);  
            }                                                
            push(ch, s2); // push operator into operator stack s2        
            flag = 0;
        }
        else 
        {
            push(ch, s1);                    
            push(' ', s1);    // we treat them as char and split them with space
        }

    }
    // pop element in s2 and push it into s1
    while(!isEmpty(s2)) 
    {       
        push(top(s2), s1);
        push(' ', s1);
        pop(s2);
    }   
}

// read expr from console till '\n' and we just only focus on '+' and '*';
// postfix expression like 6 5 2 3 + 8 * + 3 + *
char *read()
{
    char *temp;
    int len;        
    char ch;

    temp = (char*)malloc(Size * sizeof(char));
    len = 0;            
    while((ch = getchar()) != '\n') 
    {   
        if(ch == ' ')
            continue;
        temp[len++] = ch;    
    }

    temp[len] = '\0';

    return temp;
}  

// there are 2 stacks, that's operand and operator;
//works list
//1.read expr, 2.convert the expr from infix to postfix, 3.

/*
int main()
{   
    Stack operand;
    Stack operator_;
    operand = createStack(Size);
    operator_ = createStack(Size);

    // convert infix into postfix expr
    infixToPostfix(operand, operator_, read()); 
    printStack_postfix(operand);

    // compute postfix expr

    return 0;
}
*/

void infir_to_postfix()
{   
    Stack operator_;

    //create stack operand and operator_
    operand = createStack(Size);
    operator_ = createStack(Size);

    // convert infix into postfix expr
    infixToPostfix(operand, operator_, read()); 
    printStack_postfix(operand);    
}