【动态规划问题(2)】路径问题

于 2024-09-06 11:16:05 发布
阅读量1.1k 收藏 24
点赞数 15
分类专栏： # 动态规划算法 文章标签： 动态规划 算法 c++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Pau_0618/article/details/141898914
版权

文章目录

一、不同路径

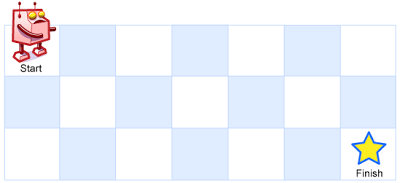
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

img

首先讲传统方法：

思路：

step1：明确dp数组及其含义

dp[i][j]的含义是到达二维数组的第 i 行第 j 列的位置，一共有多少种不同的路径。

step2：确定状态转移方程

如下图，(i, j)只能是由(i, j-1)向右过来和(i-1, j)向下过来，因此dp[i][j]的值是多少取决于到点(i, j-1)的路径总数加上到点(i-1, j)的路径总数。

即dp[i][j] = dp[i][j-1] + dp[i-1][j]

在这里插入图片描述

step3：初始化dp数组

第0行的所有位置和第0列的所有位置都是可以从原点一步走到位的，所以它们初始化为1；为什么要初始化第0行和第0列？因为后续的状态转移方程需要节点上边的元素和节点左边的元素，而第0行和第0列是边界，如果在边界运用状态转移方程会越界。

step4：确定填表顺序

dp数组从上往下填每一行，从左往右填每一列，因为我的初始状态是从第0行和第0列开始，到第m行和第n列结束

step5：确定返回值为dp[m-1][n-1]

代码表示：

int uniquePaths(int m, int n) {
    vector<vector<int>> dp(m, vector<int>(n));
    // 初始化dp数组
    for(int i = 0; i < n; i++) dp[0][i] = 1; // 第一行只有一种走法
    for(int i = 0; i < m; i++) dp[i][0] = 1; // 第一列也只有一种走法
    // 遍历dp数组
    for(int i = 1; i < m; i++) {
        for(int j = 1; j < n; j++) {
            dp[i][j] = dp[i][j-1] + dp[i-1][j];
        }
    }
    return dp[m-1][n-1];
}

添加虚拟节点的方法：

添加节点之后，我们再也不用担心填表的时候会越界了，但是虚拟节点的值一定要保证后面填表的正确，其次是要注意下标的映射关系。

在这里插入图片描述

int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m + 1, vector<int>(n + 1)); // 加1加的是虚拟节点
        // 初始化dp数组
        dp[0][1] = 1;
        // 遍历dp数组
        for(int i = 1; i <= m; i++)
            for(int j = 1; j <= n; j++)
                dp[i][j] = dp[i][j-1] + dp[i-1][j];
        return dp[m][n];
    }

显然这样的代码是不是更简单？

二、不同路径II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

在这里插入图片描述

思路：

step1：明确dp数组及其含义

dp[i][j]的含义是到达二维数组的第i行第j列的位置，一共有多少种不同的路径。

step2：确定状态转移方程

如下图，(i, j)只能是由(i, j-1)向右过来和(i-1, j)向下过来，因此dp[i][j]的值是多少取决于到点(i, j-1)的路径总数加上到点(i-1, j)的路径总数。

即dp[i][j] = dp[i][j-1] + dp[i-1][j]

但是这题相对于上题而言多了一个变化，就是遇到障碍物该怎么办，我们就将它当作0来处理，

在这里插入图片描述

step3：初始化dp数组

第0行的所有位置和第0列的所有位置都是可以从原点一步走到位的，所以它们初始化为1；但如果中途遇到了障碍物，那么我们就停止初始化，反正后面的区域我们也走不到了！

step4：确定填表顺序

dp数组从上往下填每一行，从左往右填每一列，因为我的初始状态是从第0行和第0列开始，到第m行和第n列结束

step5：确定返回值为dp[m][n]

int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
    int m = obstacleGrid.size();
    int n = obstacleGrid[0].size();
    vector<vector<int>> dp(m, vector<int>(n));
    // 初始化dp数组
    for(int i = 0; i < n && obstacleGrid[0][i] != 1; i++) {
        dp[0][i] = 1; // 第一行只有一种走法
    }
    for(int i = 0; i < m && obstacleGrid[i][0] != 1; i++) {
        dp[i][0] = 1; // 第一列也只有一种走法
    }
    // 遍历dp数组
    for(int i = 1; i < m; i++) {
        for(int j = 1; j < n; j++) {
            if(obstacleGrid[i][j] != 1) {
                dp[i][j] = dp[i][j-1] + dp[i-1][j]; // 如果上面或者左边有障碍物，没关系，也就是加0的事情
            }else continue;
        }
    }
    return dp[m-1][n-1];
}

添加虚拟节点的方法：

dp[0][1] = 1的原因是dp[1][1] == 1，也就是说机器人在原点算一种路径，而其他的虚拟节点初始化为0的原因是，dp[1][1]之后影响路劲数目的不是虚拟节点而是真实存在的节点。

在这里插入图片描述

int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1)); // +1是因为添加了虚拟节点
        // 初始化dp数组
        dp[0][1] = 1;
        // 遍历dp数组
        for(int i = 1; i <= m; i++)
            for(int j = 1; j <= n; j++)
                if(obstacleGrid[i-1][j-1] != 1) // 现在的dp[1][1]对应原来的obstacleGrid[0][0]
                    dp[i][j] = dp[i][j-1] + dp[i-1][j];
        return dp[m][n];
    }

三、珠宝的最高价值

现有一个记作二维矩阵 frame 的珠宝架，其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为：

  • 只能从架子的左上角开始拿珠宝
  • 每次可以移动到右侧或下侧的相邻位置
  • 到达珠宝架子的右下角时，停止拿取

注意：珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝，比如 frame = [[0]]。

示例 1:

输入: frame = [[1,3,1],[1,5,1],[4,2,1]]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最高价值的珠宝

思路：

step1：明确dp数组及其含义

dp[i][j]的含义是到达二维数组的第 i 行第 j 列的位置，此时的最大价值。

step2：确定状态转移方程

如下图，(i, j)只能是由(i, j-1)向右过来和(i-1, j)向下过来，因此dp[i][j]的值是多少取决于到点(i, j-1)的价值总数和到点(i-1, j)的价值总数的大值。

即dp[i][j] = max(dp[i][j-1], dp[i-1][j]) + frame[i][j]

step3：初始化dp数组

本题采用虚拟节点的方式。虚拟节点均初始化为0，由于vector的特性，所以不需要我们手动初始化了！

在这里插入图片描述

step4：确定填表顺序

dp数组从上往下填每一行，从左往右填每一列

step5：确定返回值为dp[m][n]

int jewelleryValue(vector<vector<int>>& frame) {
    int m = frame.size();
    int n = frame[0].size();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1));
    // 遍历dp数组
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            dp[i][j] = max(dp[i][j-1], dp[i-1][j]) + frame[i-1][j-1];

    return dp[m][n];
}

四、下降路径最小和

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

img

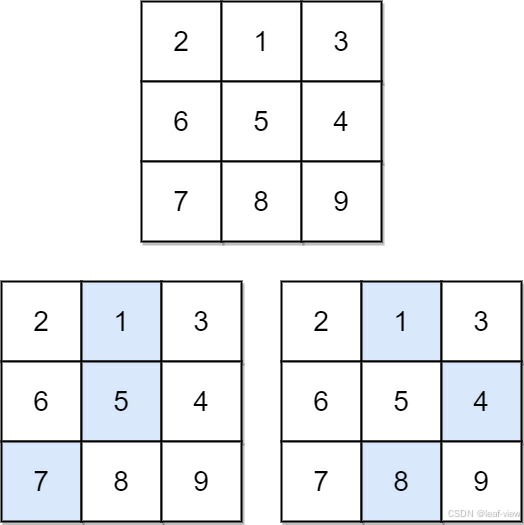
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

思路：

step1：明确dp数组及其含义

dp[i][j]的含义是到达二维数组的第i行第j列的位置时，最小的下降路径总和为多少。

step2：确定状态转移方程

dp[i][j] = matrix[i-1][j-1] + min(min(dp[i-1][j-1], dp[i-1][j]), dp[i-1][j+1])

在这里插入图片描述

step3：初始化dp数组

初始化已在上图中体现，具体是初始化虚拟节点，但是要确保后续的状态转移正确。

step4：确定填表顺序

dp数组从上往下填写每一行，因为每一行的dp值都依赖于上一行。列没有要求。

step5：确定返回值

最后一行的最小值min(dp[m][1], dp[m][2], ... ,dp[m][n]) 

int minFallingPathSum(vector<vector<int>>& matrix) {
    int n = matrix.size();
    int m = n; // 题目说是方阵
    vector<vector<int>> dp(m + 1, vector<int>(n + 2, INT_MAX));
    for(int j = 0; j < n + 2; j++) dp[0][j] = 0;
	// 初始化dp数组
    for(int i = 1; i <= m; i++)
        for(int j = 1; j <= n; j++)
            dp[i][j] = matrix[i-1][j-1] + min(min(dp[i-1][j-1], dp[i-1][j]), dp[i-1][j+1]);

    // 取最后一行的最小值
    int result = INT_MAX;
    for(int i = 1; i <= n; i++)
        result = (result > dp[m][i] ? dp[m][i] : result);

    return result;
}

五、整数拆分

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

示例 1:

输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

思路：

step1：明确dp数组及其含义

dp[i]的含义是：拆分数字 i，得到的最大乘积为dp[i]。

step2：确定状态转移方程

对于正整数 n，当 n≥2 时，可以拆分成至少两个正整数的和。
拆分成两个数：如果 j 是拆分出的第一个正整数，则剩下的部分是 n − j，n − j 不继续拆分。
拆分成两个以上的数：就要对前面的 n−j 继续拆分成至少两个正整数的和。由于每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积，因此可以使用动态规划求解。也就是说我们需要知道小的正整数对应的最大乘积，才能递推得到大的数对应的最大乘积，进而递推得到目标dp[n]。

在这里插入图片描述

step3：初始化dp数组

0拆分不成至少两个数，所以dp[0]=0；1也拆分不了，dp[1]=0；2可以拆分成1和1，所以dp[1]=1.

step4：确定填表顺序

dp数组应从前往后填表，因为我要从比n小的整数开始拆分。

step5：确定返回值为dp[n]

注意事项：

在遍历的时候，为什么不从0开始遍历？因为0的拆分毫无意义！

for(int i = 1; i <= n; i++) { // 遍历要拆分的数字
    for(int j = 1; j < i; j++) { // 固定第一个数字 
        dp[i] = max(dp[i], max(j*(i - j), j*dp[i - j]));
    }
}

上述代码可以优化成如下：

for(int i = 1; i <= n; i++) { // 遍历要拆分的数字
    for(int j = 1; j < i - 1; j++) { // 固定第一个数字 
        dp[i] = max(dp[i], max(j*(i - j), j*dp[i - j]));
    }
}

为什么？当固定的第一个数 j 等于 i - 1 时，另一个数 i - j 就是 1了，但是在开头的时候 j 已经取过了1，另一个数去过了 i - 1，这样是不是造成了重复计算。

优化2：基于数学原理，和为定值的时候，当每一个数都相等的时候，乘积有最大。我们可以让每一个数都接近相等，这样乘积才能尽可能的大！所以 j 只需要遍历到 n/2 就可以，就没有必要遍历了，一定不是最大值。这样就好像让每一个数都维持在一个中位数的范围，不会造成一个很大一个很小的数字。

for(int i = 1; i <= n; i++) { // 遍历要拆分的数字
    for(int j = 1; j <= i / 2; j++) { // 固定第一个数字 
        dp[i] = max(dp[i], max(j*(i - j), j*dp[i - j]));
    }
}

最终代码：

int integerBreak(int n) {
    if(n <= 1) return 0;
    vector<int> dp(n+1);
    // 初始化dp数组
    dp[0] = dp[1] = 0;
    dp[2] = 1;
    for(int i = 1; i <= n; i++) { // 遍历要拆分的数字
        for(int j = 1; j <= i/2; j++) { // 固定第一个数字 
            dp[i] = max(dp[i], max(j*(i - j), j*dp[i - j]));
        }
    }
    return dp[n];
}

六、不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

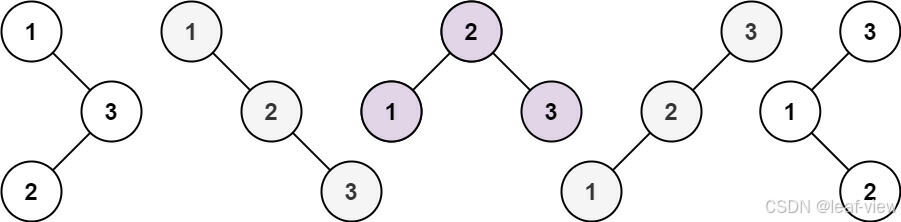
在这里插入图片描述

输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

解题步骤：

step1：明确dp数组及其含义

综上可知，dp[i]表示有i个节点时，搜索树的种数，题目要求dp[n].

step2：确定状态转移方程
首先分析前三个节点，即当n=1,2,3时，搜索树的个数：

在这里插入图片描述

  • n=1时，有一个头结点，只有一种二叉搜索树；
  • n=2时，有两个头结点，一个是以1为头结点（左子树由空组成(dp[0])，右子树由1个节点组成(dp[1])）；一个是以2为头结点（左子树为1个节点(dp[1])，右子树由1个节点组成(dp[0])）；
    二叉搜索树的总数为：1为头结点的二叉树 + 2为头结点的二叉树 = dp[0]*dp[1] + dp[1]*dp[0]
  • n=3时，二叉搜索树的总数为：
    1为头结点的二叉树 + 2为头结点的二叉树 + 3为头结点的二叉树 = dp[0]*dp[2] + dp[1]*dp[1] + dp[2]*dp[0]

当N = n(n = 1,2,3…)时，依次将1到n作为根节点，计算出各个节点作为根的时候的搜索树的个数，再将这些二叉搜索树加起来即为dp[n]。然后每次计算的时候都是需要前一个节点数目的递推关系才能够得到。

// i为节点的总数
for(int i = 1; i <= n; i++){
    // 遍历节点1到n，将其作为根节点
    for(int j = 1; j <= n; j++){
        dp[i] += dp[i-1]*dp[i-j]; // 根节点i的左树有dp[i-1]种，右树有dp[i-j]种
    }
}

step3：初始化dp数组

0个节点认为也是1个搜索树，否则0乘任何数都为0了没有意义，所以dp[0]=1；由图可知，dp[1]=1，dp[2]=2.

step4：确定填表顺序

dp数组应从前往后填表，因为状态转移方程需要下标较小的dp数组递推得到。

step5：确定返回值为dp[n]

代码：

int numTrees(int n) {
    vector<int> dp(n+1);
    dp[0] = 1;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= i; j++){
            dp[i] += dp[j-1] * dp[i-j];
        }
    }
    return dp[n];
}

七、最小路径和

在这里插入图片描述

dp[i][j]含义：从左上角到(i, j)位置的最小路径和。
方法一：

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        // 创建dp数组
        vector<vector<int>> dp(m, vector<int>(n));
        // 初始化dp数组
        dp[0][0] = grid[0][0];
        for(int i = 1; i < n; i++) // 初始化行
            dp[0][i] = dp[0][i-1] + grid[0][i];
        for(int i = 1; i < m; i++) // 初始化列
            dp[i][0] = dp[i-1][0] + grid[i][0];
		// 状态转移方程
        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                dp[i][j] = grid[i][j] + min(dp[i][j-1], dp[i-1][j]);
            }
        }
        return dp[m-1][n-1];
    }
};

方法二：创建虚拟dp表
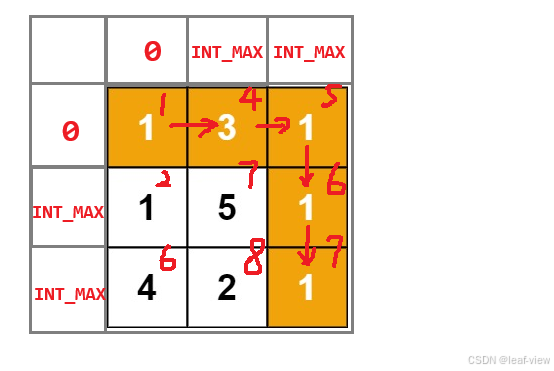
在这里插入图片描述

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 200));
        dp[0][1] = dp[1][0] = 0;
        for(int i = 1; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                dp[i][j] = grid[i-1][j-1] + min(dp[i][j-1], dp[i-1][j]);
            }
        }
        return dp[m][n];
    }
};

八、地下城游戏

解题步骤：

step1：明确dp数组及其含义

这道题根据以往的经验“dp数组的含义：以什么位置为结尾，…”是行不通的。用在这题当中，dp[i][j]：以(i, j)位置为结尾最低初始健康点数，那么骑士在前往下一个房间健康值就可能会<=0.
我们逆向思维，如果 dp数组的含义为：以什么位置为起点，… 会怎么样呢？
用在这题当中，dp[i][j]：以(i, j)位置为起点到达右下角的最低初始健康点数。显然是能行得通的，如当我们处于公主被关押的位置，最低初始健康点数应该为：1 - dungeon[m-1][n-1] > 0。

step2：确定状态转移方程
在这里插入图片描述

step3：初始化dp数组

考虑到以(m-1,n-1)为起点，向右和向下移动一步的情况会造成越界的情况，dp数组应多开一行一列。最后要对这多开的一行一列初始化，以满足填表的正确性。
在这里插入图片描述

step4：确定填表顺序

dp数组应从右下角往左上角填表。

step5：确定返回值为dp[0][0]

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        // 创建dp表
        int m = dungeon.size(), n = dungeon[0].size();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));
        // 初始化dp表
        dp[m][n-1] = dp[m-1][n] = 1;
        // 动态规划
        for(int i = m - 1; i >= 0; i--)
            for(int j = n - 1; j >= 0; j--)
                dp[i][j] = max(min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j], 1);

        return dp[0][0];
    }
};

时间复杂度：O(m * n)
空间复杂度：O(m * n)

动态规划：不同路径
m0_54187478的博客
04-30 458
一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start”）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。问总共有多少条不同的路径？例如，一个 7 x 3 的网格有多少可能的路径？dp[i][j]表示从起点到达点 (i, j) 的路径总数。，表示机器人可以从上方或左方移动到 (i, j)。dp[0][j]dp[i][0]dp[0][0]这段代码实现了前面描述的动态规划方法，通过两重循环来计算每个格点的路径数，最终结果存储在中。
leetcode-62-不同路径
shadowgully的博客
12-09 136
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。 问总共有多少条不同的路径？ [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vhMGVVKn-1607527207480)( https://assets.leetcode.com/uploads/2018/10/22/robot_maze.png)] 示例 1： 输入：m = 3,
动态规划——不同的路径
IFollowRivers
06-19 1004
题目链接：http://www.lintcode.com/zh-cn/problem/unique-paths/ 参考资料：http://blog.csdn.net/derrantcm/article/details/47182719 public class UniquePaths { public static void main(String[] args) { // T
Leetcode 62. 不同路径（简单DP）
阳光大男孩！！！的博客
08-07 285
题目重述 一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。 问总共有多少条不同的路径？ 示例 1： 输入：m = 3, n = 7 输出：28 示例 2： 输入：m = 3, n = 2 输出：3 解释： 从左上角开始，总共有 3 条路径可以到达右下角。 向右 -> 向下 -> 向下 向下 -> 向下 -> 向右 向下 -> 向右
动态规划--不同的路径
yong_zi的博客
08-12 3647
114. 不同的路径 有一个机器人的位于一个 m × n 个网格左上角。 机器人每一时刻只能向下或者向右移动一步。机器人试图达到网格的右下角。 问有多少条不同的路径？ 样例 给出 m = 3 和 n = 3, 返回 6. 给出 m = 4 和 n = 5, 返回 35. 注意事项 n和m均不超过100 解题思路：终于自己做出了一道这样的题目（这次没有参考），是真的开心。 刚做这个...
dongtaiguihua.rar_动态规划程序_动态规划问题_求最短路径_路径规划
09-19
在给定的“dongtaiguihua.rar”压缩包文件中，我们可以找到一个关于动态规划求解最短路径问题的程序，这对于我们理解和应用动态规划具有极大的价值。 动态规划的核心理念是将复杂的问题分解为相互关联的子问题，并...
多段图的最短路径问题 动态规划法——C++代码
05-24
本主题关注的是多段图的最短路径问题，通过动态规划法来求解。动态规划是一种利用子问题的最优解来构建全局最优解的算法设计策略，适用于解决具有重叠子问题和最优子结构的问题。 多段图是指一个图中的边不再仅连接...
算法沉淀 —— 动态规划篇（路径问题）
最新发布
Zhenyu_Coder的博客
03-26 2076
几乎所有的动态规划问题大致可分为以下5个步骤，后续所有问题分析都将基于此1.、状态表示：通常状态表示分为以下两种，其中更是第一种为主。以i为结尾，dp[i] 表示什么，通常为代求问题（具体依题目而定）以i为开始，dp[i]表示什么，通常为代求问题（具体依题目而定）2、状态转移方程*以上述的dp[i]意义为根据， 通过最近一步来分析和划分问题，由此来得到一个有关dp[i]的状态转移方程。3、dp表创建，初始化动态规划问题中，如果直接使用状态转移方程通常会伴随着越界访问等风险，所以一般需要初始化。
dongtaiguihua.rar_动态规划 最短路径_动态规划 路径_最短路径规划_路径规划
09-14
在这个主题中，我们将深入探讨如何使用动态规划来求解最短路径问题，以及如何通过2.cpp文件中的示例代码来理解这一过程。 一、动态规划简介 动态规划是由美国数学家理查德·贝尔曼在20世纪50年代提出的，它是一种...
动态规划经典题目及答案
01-25
关于动态规划的一些经典题目，有助于提高编程能力，对于学习有很大的准备，，！！！期待大家学习分享！
动态规划经典题目及解答整理
05-17
动态规划经典题目及解答（含代码pdf） 1． 最长公共子序列 2． 计算矩阵连乘积 3． 凸多边形的最优三角剖分 4． 防卫导弹 5． 石子合并 6． 最小代价子母树 7． 商店购物 8． 旅游预算 9． 皇宫看守 10． 游戏室问题 11． *基因问题 12． *田忌赛马
不同路径2
vclearner2的博客
09-03 199
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。 现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？ 网格中的障碍物和空位置分别用 1 和 0 来表示。 说明：m和 n 的值均不超过 100。 示例1: 输入: [ [0,...
【动态规划】不同的路径
qiulig
07-04 361
1.题目描述 一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。 问总共有多少条不同的路径？ 2.解题思路 动态规划 （1）初始化 1) 从[0,0]走到[0,0]的路径，即没走，设dp[0][0] = 0; 2) 如果m*n的n为...
动态规划之不同路径
qq_21313581的博客
02-10 253
动态规划，相信对于一些刚学习算法的朋友来说，动态规划是算法在最难以理解，和自己设计时都苦恼。现在，我就以这题来给大家伙们讲。
不同路径——动态规划
weixin_44891861的博客
02-13 657
文章目录题目一：不同路径解法一：动态规划优化一优化二解法二：数学题目二：不同路径II 题目一：不同路径 一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。 问总共有多少条不同的路径？ 解法一：动态规划 本题目使用动态规划来解决比较简单，定义dp[i][j]数组为到达(i，j)点的路径数。由题中所述机器人只能向下向右走，可得递推公式为 dp[i][j]=dp[i−1
动态规划之不同路径 ||
friendship1998的博客
05-08 118
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。 现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？ 网格中的障碍物和空位置分别用 1 和 0 来表示。 示例： 代码： public int uniquePathsWithObstacles(int[][] obstacleGrid) { int m=obstacleGrid.le
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值