微分方程模型不便于分析结构或参数变化对系统性能的影响,所以我们便引入复数域的数学模型–传递函数。
传递函数定义
线性定常系统的传递函数,是零初始条件下系统输出 量的拉氏变换与系统输入量的拉氏变换之比。
条件
线性定常系统
零初始条件(1.系统的输入在t>0时才作用于系统。即在t=0时系统输 入及其各项导数均为零。 2.输入在加于系统之前,系统为稳态。即在t=0时输出及 其所有导数为零。)
传递函数的标准形式

n>=m
系统的特征多项式:分母多项式。
系统的特征方程:N(s)=0
系统的极点(特征根): N(s)=0的根。
系统的零点: M(s)=0的根。
系统的阶次:分母多项式的阶次。
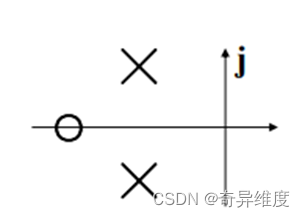
零极点分布图
在复数平面上,用○表示零点,用╳表示极点。
传递函数与微分方程
将微分方程算符d/dt用复数s置换可 以得到传递函数。

性质
传递函数反映系统自身固有特性,与输入和初始条件无关。
不同的物理系统可能有相同的传递函数,而同一系统可以有不同的传递函数。
传递函数与单位脉冲响应之间是拉氏变换与拉氏反变换的关系。
例题

典型环节传递函数
比例环节
积分环节
惯性环节(非周期环节)
振荡环节
微分环节
理想微分环节(与积分环节对应)
一阶微分环节(与惯性环节对应)
二阶微分环节(与振荡环节对应)
延迟环节


























 800
800

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










