红黑树 图解快速入门

这篇文章会简单介绍一下红黑树这种数据结构。
在阅读本文章之前，读者最好先理解二叉树、二叉搜索树、自平衡二叉搜索树的概念。

什么是红黑树？

红黑树是一种特殊的二叉搜索树。

二叉搜索树的特点：

1. 对于树中每一个节点，左儿子节点值小于它本身，右儿子节点值大于它本身
2. 二叉搜索树中序遍历得到的序列是递增有序序列

下图是一棵二叉搜索树：

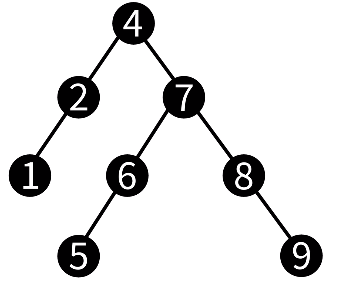
二叉搜索树的查找、插入、删除的时间复杂度都是O(h)，h代表树高。

在极端情况下，二叉搜索树会退化成一条链表：

此时三种操作的时间复杂度都退化为O(N)，N为节点数

为了控制树高，这时候我们需要平衡树。平衡树的操作时间复杂度是O(logN)，N为节点数

红黑树也是一种平衡的二叉搜索树

红黑树的特点

1. 每个节点要么是红色，要么是黑色
2. 根节点和叶节点是空节点 (nil) 且都是黑色的
3. 如果一个节点是红色的，那么他的孩子是黑色的（也就是说，不会出现两个红色节点相邻的情况）
4. 任意节点到叶子节点的路径中包含相同数量的黑节点

下图是一棵红黑树：

红黑树的查找、插入、删除的时间复杂度都是O(logN)

注意：在以下图中的树是红黑树中的一部分，并不是完整的一棵红黑树，我们通过红黑树中的部分来演示各种操作。
 

红黑树的变色和旋转操作

为什么需要变色和旋转？
因为红黑树的插入和删除操作可能导致树变为不符合红黑树的性质特征，这时候就需要通过变色和旋转来维持红黑树的性质

变色操作

变色操作其实很好理解，就是将节点的颜色进行变换

变色前：

变色后：

旋转操作

旋转操作与自平衡二叉搜索树一样，分左旋和右旋操作且一致。

下图示例左旋操作，将节点4进行左旋

左旋操作前：

左旋操作后：

旋转操作的特点：

1. 旋转操作不会改变树中序遍历的顺序
2. 旋转操作通过降低高度高的子树的高度，增加高度低的子树的高度来维护二叉树的平衡
    

红黑树的插入操作

为方便阐述插入操作过程，这里引入家族名称，以节点6为例：

红黑树的插入分为两个过程，一个是插入过程，一个是修复过程

插入过程

基本与二叉搜索树一致，不同点在于插入的节点会标记会红色

修复过程

当我们在红黑树中插入一个节点后，会出现以下四种情况：

1. 新插入节点是根节点（即插入节点前是一棵空树）
2. 新插入节点的叔叔节点是红色的
3. 新插入节点的叔叔节点是黑色的，并且局部呈现直线
4. 新插入节点的叔叔节点是黑色的，并且局部呈现三角形

针对这四种不同情况有以下四种不同的应对操作

情况一：新插入节点是根节点

依据红黑树根节点和叶子节点(nil)是黑色的特点，我们只需将新插入节点颜色变换为黑色即可

情况二：新插入节点的叔叔节点是红色的

依据红黑树红色节点不相邻的特点，我们将新插入节点的叔叔节点、父亲节点、祖父节点进行变换颜色：

注意这里是递归调用的，即当改变了新插入节点的相关节点的颜色后，可能导致上层就不符合红黑树的特点了，这时候也需要接着修改上层节点的颜色。

如果A是根节点，为了满足红黑树根节点是黑色的特点，我们只需要将根节点再次进行变换颜色即可

情况三：新插入节点的叔叔节点是黑色的，并且局部呈现直线

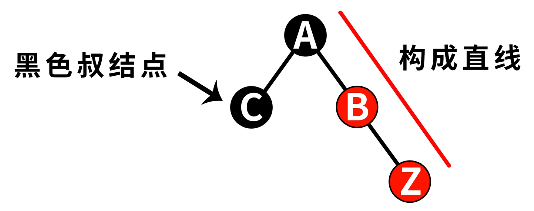
构成直线的意思是，新插入节点与其父节点、祖父节点形成直线。

（注意按上图这个情况，C节点其实是叶节点，即nil节点）

这种情况下我们需要进行以下两个步骤

1. 旋转新插入节点的祖父节点
2. 将新插入节点的父节点和祖父节点进行变换颜色

在本例中，先对新插入节点的父节点进行旋转，旋转的方向与直线的朝向相反：

• 当直线斜向右下方时，对父节点节点进行左旋
• 当直线斜向左下方时，对父节点节点进行右旋

在本例中，我们需要对祖父节点进行左旋，得到：

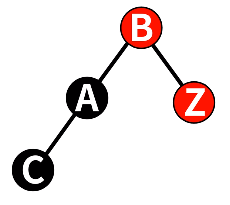
紧接着，我们对新插入节点的父节点和祖父节点进行颜色变换，即可得到满足红黑树性质的树。

情况四：新插入节点的叔叔节点是黑色的，并且局部呈现三角形

这种情况下我们需要先将父节点进行旋转，得到：

这个情况下与情况三一致，接着按照情况三的操作方式进行操作。

红黑树的删除操作

红黑树的删除也分为两个过程，一个是删除过程，一个是修复过程

删除过程

在删除过程中，无需关心红黑树的节点颜色情况，与二叉搜索树的删除操作一致。

二叉搜索树的删除操作在这里简要说一下，主要分三种情况：

1. 被删除节点不具有子节点，此时直接移除该节点即可
2. 被删除节点只有一个子节点，此时使用该子节点替代删除节点的位置即可
3. 被删除节点有两个子节点，这时候我们在被删除节点的右子树中找到最靠左的节点（即被删除节点的后继节点），用该节点替代被删除节点的位置即可

可以在我的这篇文章《二叉搜索树类题目专题训练 – LeetCode上10道与二叉搜索树相关的题》中的第七题做与二叉搜索树删除操作相关的题目。

修复过程

修复过程分两种情况：

1. 被删除节点为红色节点
2. 被删除节点为黑色节点

不难发现，删除红色节点，并不会使得删除节点后的树不满足红黑树的性质，因此我们只需要考虑删除黑色节点的情况。

删除节点为黑色节点需要分情况讨论，以下图为例

设节点X为取代被删除节点后的节点，则我们需要依据节点X的兄弟节点W来进行分情况讨论：

1. 删除节点的兄弟节点为黑色节点，且其子节点都是黑色节点
2. 删除节点的兄弟节点为黑色节点，其右子节点为红色节点
3. 删除节点的兄弟节点为黑色节点，其左子节点为红色节点，右子节点为黑色节点
4. 删除节点的兄弟节点为红色节点

情况一：删除节点的兄弟节点为黑色节点，且其子节点都是黑色节点

由于删除操作让删除节点路径上的黑色高度 - 1，所以我们将其兄弟节点(W)变为红色，以保持A以下的局部黑色高度平衡。

但这样树的整体仍然可能黑色高不平衡，所以将删除节点的父节点(A)作为对象继续迭代到修复算法中。直到迭代对象变为根节点或者红色。

情况二：删除节点的兄弟节点为黑色节点，其右子节点为红色节点

这个情况要分三步进行：

1. 将删除节点的兄弟节点颜色设为与父节点一致
   
2. 将删除节点的兄弟节点的父节点与子节点的颜色反转
   
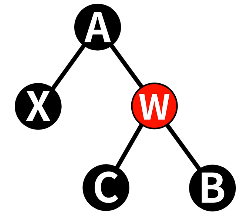
3. 将删除节点的父节点进行旋转，在此例中进行左旋
   

情况三：删除节点的兄弟节点为黑色节点，其左子节点为红色节点，右子节点为黑色节点

这个情况要分三步进行：

1. 先交换删除节点的兄弟节点与其左儿子节点的颜色
   
2. 将删除删除节点的兄弟节点进行旋转，在此例中进行右旋
   
3. 这样，就变为与情况二一致，依据情况二进行操作

情况四：删除节点的兄弟节点为红色节点

这个情况要分三步进行：

1. 先将删除节点的兄弟节点与父节点颜色交换
   
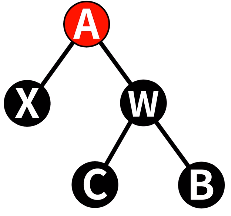
2. 将父节点进行旋转，在此例中进行左旋
   
3. 这时候红黑树会转换为以上三种情况中的一种，按其情况进行操作

都看到这里了，喜欢本篇文章的话不妨点个赞再走吧 😃

内容参考自B站up主 谢某人er
参考视频：https://www.bilibili.com/video/BV18y4y1m721/?spm_id_from=333.788.recommend_more_video.0