第六章:分类问题
把线性回归用于分类问题,不是一个好方法 —— 癌症的例子,增加一个特别容易判断的例子,反而影响了中间那部分的判断
logistic回归算法 - 逻辑回归算法
是一种分类算法
假设函数的表示方法
sigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。
h
θ
(
x
)
=
1
1
+
e
−
θ
T
x
h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}
hθ(x)=1+e−θTx1
我们假设
h
θ
(
x
)
≥
0.5
h_\theta(x) \geq 0.5
hθ(x)≥0.5 则预测
y
=
1
y=1
y=1,即
θ
T
x
≥
0
\theta^Tx\geq0
θTx≥0
决策边界——是假设函数的一个属性,决定于假设函数(参数),不取决于数据集
如何拟合logistic模型的参数 θ \theta θ
首先要定义用来拟合参数的优化目标(代价函数)
整个模型:
我们有个训练集training set ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋅ ⋅ ⋅ , ( x ( m ) , y ( m ) ) {(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),···,(x^{(m)},y^{(m)})} (x(1),y(1)),(x(2),y(2)),⋅⋅⋅,(x(m),y(m))
有m个样本examples,
x
∈
[
x
0
x
1
⋅
⋅
⋅
x
n
]
x\in \begin{bmatrix} x_0\\ x_1\\ ···\\ x_n \end{bmatrix}
x∈⎣⎢⎢⎡x0x1⋅⋅⋅xn⎦⎥⎥⎤
其中
x
0
=
1
,
y
∈
{
0
,
1
}
x_0 = 1,y\in \{0,1\}
x0=1,y∈{0,1}
假设函数
h
θ
(
x
)
=
1
1
+
e
−
θ
T
x
h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}
hθ(x)=1+e−θTx1
那么我们如何选择参数
θ
\theta
θ?
我们定义一个代价函数,对于某个
x
i
x_i
xi ,利用假设函数
h
(
x
i
)
h(x_i)
h(xi)计算出预测值,和真实值(标签)进行比较,如差的平方的一半的平均,对于所有样本都这样算,采用算数平均:
J
(
θ
)
=
1
m
∑
i
=
1
m
1
2
(
h
θ
(
x
i
)
−
y
i
)
2
J(\theta) = \frac{1}{m}\sum_{i=1}^m{\frac{1}{2}(h_\theta(x_i)-y_i)^2}
J(θ)=m1i=1∑m21(hθ(xi)−yi)2
——但是这种方法,是非凸函数,在使用梯度下降的时候,容易陷入局部最优问题
所以,我们要找一个凸函数:
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
{
−
l
o
g
(
h
θ
(
x
)
)
i
f
y
=
1
−
l
o
g
(
1
−
h
θ
(
x
)
)
i
f
y
=
0
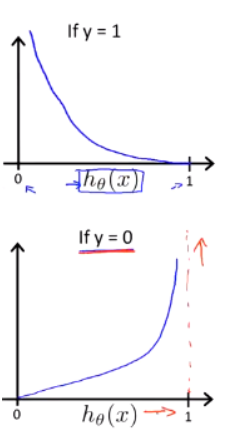
Cost(h_\theta(x),y) = \left \{ \begin{aligned} -log(h_\theta(x))\quad if\: y = 1\\ -log(1-h_\theta(x))\quad if\: y = 0 \end{aligned} \right.
Cost(hθ(x),y)={−log(hθ(x))ify=1−log(1−hθ(x))ify=0
在这个代价函数中,当y确实为1,而我们预测的
h
θ
(
x
)
h_\theta(x)
hθ(x)也趋近于1,则代价函数值很小;而y确实为1时,我们预测的
h
θ
(
x
)
h_\theta(x)
hθ(x)也趋近于0,那么代价函数值就很大,说明当前的参数不好,我们预测的不好,代价函数大。反之类似。
如何利用梯度下降法来拟合logistic回归的参数
上面的cost函数要分情况,我们想办法写在一起
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
l
o
g
(
1
−
h
θ
(
x
)
)
Cost(h_\theta(x),y) =-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))
Cost(hθ(x),y)=−ylog(hθ(x))−(1−y)log(1−hθ(x))
——是凸函数
接下来要找到参数 θ \theta θ 使得 m i n J ( θ ) minJ(\theta) minJ(θ)最小
重复:
θ
j
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
)
\theta_j :=\theta_j - \alpha \frac{\partial}{\partial\theta_j} J(\theta)
θj:=θj−α∂θj∂J(θ)
代入
J
(
θ
)
J(\theta)
J(θ),得:
θ
j
:
=
θ
j
−
α
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\theta_j :=\theta_j - \alpha \sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
θj:=θj−αi=1∑m(hθ(x(i))−y(i))xj(i)
这个式子虽然是一行,但是
θ
\theta
θ是n+1维的,使用for循环,i = 0 - > n
高级优化算法
优化算法
- Gradient descent 梯度下降
- Conjugate gradient
- BFGS 共轭梯度法
- L-BFGS
后面三个算法:
-
不用手动设置学习率 α \alpha α
有个智能内循环clever inner-loop,称为 线搜索算法 line search algorithm
-
收敛速度远远快于梯度下降
-
缺点:更复杂
直接使用软件库,调用别人写好的函数
使用logistic解决多类别分类问题-”一对多“的分类算法

相当于是有三个分类器,为了实现预测,将x输入,求出三个 h θ ( i ) h_\theta^{(i)} hθ(i),挑选出最大的






















 8823
8823











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








