基本的快速排序
最基本的快速排序是由C.A.R.Hoare在1960年提出的,快速排序的算法是一种分治排序算法
它将数组划分为两个部分,然后分别对两个部分进行排序
快速每次对数组重新排序,选择一个基准值key,然后让数组满足下面的两个个条件
·a[l], ... ,a[i - 1]之中的元素都比key值要小
·a[i + 1], ... ,a[r]之中的元素都比key值要大
然后通过划分来完成排序,递归的去处理子文件,这就是快速排序
快速排序代码如下:
void QuickSort(int arr[], int left, int size) {
if (arr == NULL || size <= 0) {
//对参数合法性进行检查
return;
}
if (size - left <= 1) {
/*子区间已经有序了*/
return;
}
//前闭后开的区间
int mid = partition(arr, left, size);
//递归的处理
QuickSort(arr, left, mid);
QuickSort(arr, mid + 1, size);
}其中的partition函数是对当前数组进行划分,函数的代码如下:
int partition(int arr[], int left, int right) {
assert(arr);
int _left = left;
int _key = right - 1;
int _right = right - 1 - 1;
while (_left < _right) {
/*
**从左往右找出第一个大于arr[key]的值
*/
while (arr[_left] <= arr[_key]) {
++_left;
}
/*
**从右往左找出第一个小于arr[key]的值
*/
while (arr[_right] >= arr[_key]) {
if (_right == _left) {
/*
**在从右往左找大于key值得元素时,遇到了_left
*/
break;
}
--_right;
}
/*
**在这里再次进行判断
*/
if (_left >= _right) {
break;
}
Swap(&arr[_left], &arr[_right]);
}
if (arr[_left] > arr[_key]) {
Swap(&arr[_left], &arr[_key]);
}
return _left;
}
这是对数组进行划分的函数,具体操作如下:
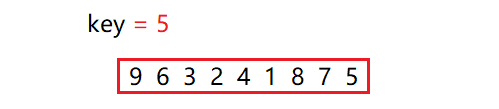
首先以数组最右边的元素为基准key值,一般都是最左边或者最右边
如上图,以5为基准值,然后定义一个_left下标和 _right下标
_left从左往右找出大于key的元素,_right找出小于key的值,然后进行 交换
第一次交换了9和1,然后再继续循环,如图
这次是交换了4和6,再继续循环,_left和 _right在6的下面相遇,此时_left == _right,然后退出循环
注意,退出循环后应该判断当前元素和基准值的大小,如果大于基准值也要交换,这点很重要,如图:
对数组的第一次划分到这里就结束了,一次完成后,基准值key之前的元素都小于key,而之后的元素都大于key,这
样继续递归,就可以对数组进行排序了,而这也是最基础的快速排序
对快速排序算法的改进
尽管基本的快速排序已经 很有用处了,但是有些情况下,基本的快速排序可能会极为低效,比如排序一个大小为N的
有序文件,这样所有的划分就会退化,程序会调用自身N次,所以
·快速排序最坏情况下使用大约(N^2)/2次比较
我们可以对快速排序进行改进,有以下几种方法:
1.切换到插入排序
通过观察可见,快速排序的递归调用自身许多的小文件,所以我们可以在遇到小的子文件的时候可以用更好的方法,以此来对快速排序进行改进,比如在子文件小于某个值M时进行插入排序,方法就是把递归出口的条件换成下面这样:
if (size - left <= M) {
/*子区间已经有序了*/
insertition(arr, left, right);
return;
}2.三者取中划分
对快速排序算法的另一种改进就是使用一个尽可能再文件中间划分为元素,即基准值key的大小最好是在待排序文件中不大不小
有以两种思路:
·一种是避免最坏的情况,使用数组中的一个随机元素作为划分元素,这样出现最坏情况的几率就会相对很小
·一种是从文件中取出三个元素,使用三个元素的中间元素作为划分元素
我们这里用的是第二种思路方法,取出数组的左边元素,中间元素和右边元素,然后对这三个元素进行排序,然后以中间的元素作为基准值key
代码如下:
void CompExch(int* a, int* b) {
if (*a > *b) {
Swap(a, b);
}
}
void _QuickSort(int arr[], int left, int right) {
assert(arr);
if (right - left <= MIN) {
return;
}
int i = left + (right - left) / 2;
Swap(&arr[i], &arr[right - 1]);
CompExch(&arr[left], &arr[right - 1]);
CompExch(&arr[left], &arr[right]);
CompExch(&arr[right - 1], &arr[right]);
int mid = partition(arr, left + 1, right - 1);
_QuickSort(arr, left, mid);
_QuickSort(arr, mid + 1, right);
}还是上面那一组数据,如图:
首先进行如下的操作,把中间的元素和倒数第二个元素进行交换,如图
完成之后,进行如下操作,
CompExch(&arr[left], &arr[right - 1]);
CompExch(&arr[left], &arr[right]);
把左边的值和右边的一交换,这样,最左边的值就会是三个值中的最小的值了,然后再把倒数第一个和的倒数第二个元素进行比较交换,选出其中的中间元素作为基准值,
CompExch(&arr[right - 1], &arr[right]);
这样,这三个数就是有序的了,然后再进行快速排序的处理,这样可以保证不会出现基准值偏差太大的情况
其实这也是用到了数学方面的思想,对未知文件进行采样,然后用样本元素的性质来估算整个文件的性质
三者取中法比较均衡,如果选择更多的样本,虽然可以得到一个好的划分,但是改进的时间被取样的时间抵消了
3.三路划分的快速排序
我们上面的样本没有出现有大量重复关键字的情况,但是这种情况在实际中很常见,那么我们如何改进呢?
一种直接的方法是将文件划分成三个部分:一部分比划分元素小,一部分比划分元素大,还有一部分等于划分元素,如图:
完成这样的过程比两路划分更为复杂,Bentley和Mcllory于1993年发明了一种三路划分的方法:它把标准的划分过程做了如下改进:扫描时把遇到的左子文件中与基准值key相等的元素放到文件的最左边,然后把右子文件中与划分元素相等的元素放到文件的最右边,如图;
即使在没有重复关键字的时候,该方法也会运行的很好
代码如下:
void QuickSort(int arr[], int left, int right) {
assert(arr);
if (left >= right) {
return;
}
int l = left - 1, r = right, value = arr[right];
int p = left - 1;
int q = right;
while (1) {
//向左向右扫描找到不小于value的值
while (arr[++l] < value) { ; }
//从右向左扫描找到不大于value的值
while (arr[--r] > value) { if(r == left) break; }
if (l >= r) {
break;
}
Swap(&arr[l], &arr[r]);
//如果arr[l]的值和value是相等的,就把它放入到数组左边
if (Eq(arr[l], value)) {
p++;
Swap(&arr[p], &arr[l]);
}
//同理,把和value相等的值放入到数组右边
if (Eq(arr[r], value)) {
q--;
Swap(&arr[q], &arr[r]);
}
}
/*上面的循环找到了需要的元素,然后交换*/
Swap(&arr[l], &arr[right]);
r = l - 1; l = l + 1;
int k = 0;
//把相等的元素都交换到数组的中间
for (k = left; k <= p; ++k, --r) {
Swap(&arr[k], &arr[r]);
}
for (k = right - 1; k >= q; --k, ++l) {
Swap(&arr[k], &arr[l]);
}
QuickSort(arr, left, r);
QuickSort(arr, l, right);
}
以下面的数据为例子:
选出基准值key = 3, 然后进行划分,划分完成后如下:
我用红色标出3这个元素,第一次划分完成后,现在j = 2, i = 4
for (k = left; k <= p; ++k, --r) {
Swap(&arr[k], &arr[r]);
}
for (k = right - 1; k >= q; --k, ++l) {
Swap(&arr[k], &arr[l]);
}由于右边没有进行交换,所以q = right,而p由于只交换了一次,所以p = left,这时候arr[r] = 1,所以两个一交换,就完成了,如图:
然后再递归的进行处理,就完成了快速排序
这种方法是处理文件中有大量的重复元素的情况,性能会比基本的快速排序好很多
好了,就总结到这里




















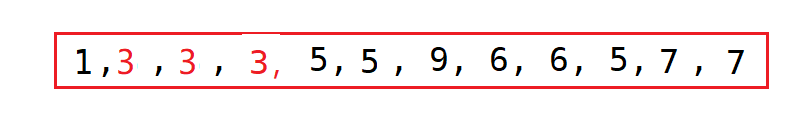














 753
753

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








