主成分分析（PCA）原理总结

欢迎关注天善智能，我们是专注于商业智能BI，人工智能AI，大数据分析与挖掘领域的垂直社区，学习，问答、求职一站式搞定！

对商业智能BI、大数据分析挖掘、机器学习，python，R等数据领域感兴趣的同学加微信：tstoutiao，邀请你进入数据爱好者交流群，数据爱好者们都在这儿。

作者：张磊 从事AI医疗算法相关工作

个人微信公众号：

机器学习算法那些事（微信ID：zl13751026985

主成分分析（Principal components analysis，以下简称PCA）是最常用的降维方法之一，在数据压缩和消除冗余方面具有广泛的应用，本文由浅入深的对其降维原理进行了详细总结。

目录

---

1.向量投影和矩阵投影的含义

2. 向量降维和矩阵降维的含义

3. 基向量选择算法

4. 基向量个数的确定

5. 中心化的作用

6. PCA算法流程

7. PCA算法总结

1. 向量投影和矩阵投影的含义

如下图：

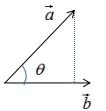
向量a在向量b的投影为：

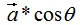
其中，θ是向量间的夹角 。

向量a在向量b的投影表示向量a在向量b方向的信息，若θ=90°时，向量a与向量b正交，向量a无向量b信息，即向量间无冗余信息 。因此，向量最简单的表示方法是用基向量表示，如下图：

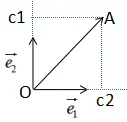
向量表示方法：

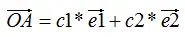
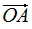
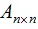
，其中ai（i=1,2,...,n）为n个维度的列向量，那么矩阵A的列向量表示为：

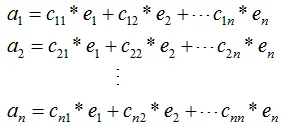
其中，e1，e2，...，en为矩阵A的特征向量 。

若矩阵A是对称矩阵，那么特征向量为正交向量，我们对上式结合成矩阵的形式：

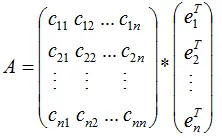
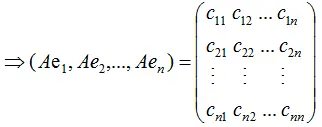
由上式可知，对称矩阵A在各特征向量的投影等于矩阵列向量展开后的系数，特征向量可理解为基向量。

2. 向量降维和矩阵降维含义