文章目录
在之前学习的过程中我了解到深度学习中很重要的一个概念是反向传播,最近看论文发现深度强化学习(DRL)有各种各样的方法,但是却很难区分他们的损失函数的计算以及反向传播的过程有何不同。在有监督的学习中,损失可以理解为预测值和真实值之间的距离,那么在这里的损失指的是什么?是否也涉及到两个值之间的差距呢,具体是哪两个东西之间的拟合(学习)?如何拟合?这里通过举例对几种强化学习方法进行比较。
下图是强化学习的分类:
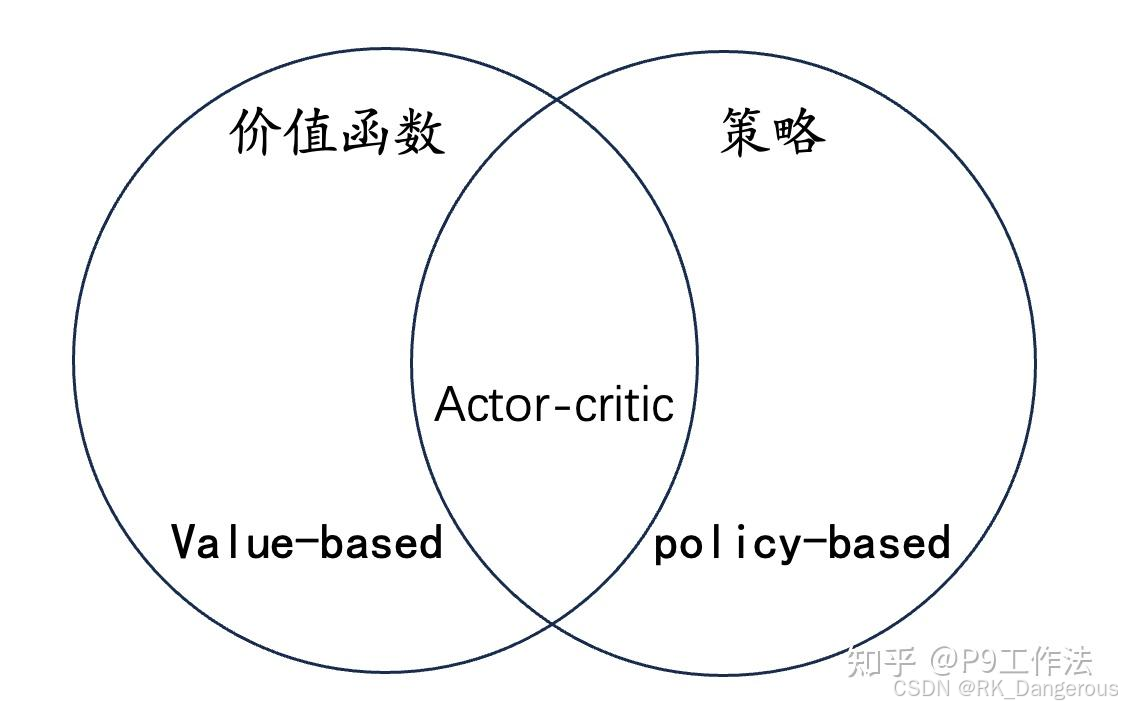
1、基于价值的强化学习:学习价值函数,从价值函数中获得隐式的策略。
2、基于策略的强化学习:没有价值函数,直接学习策略。
3、Actor-Critic框架:同时学习策略和价值函数。
在我的理解里,基于价值的强化学习,就是得到每个动作的概率(价值),然后选择动作的最大值作为最后的结果,看起来也像是学习了策略。所以不通过实例,很难区分基于价值的和基于策略的二者有什么区别。
一、深度强化学习知识框架
根据上述介绍可知,深度强化学习方法可分为三大类,分别以不同方式建模和优化智能体的决策行为,如下总结了这三大类方法和其他方法:
| 类别 | 核心思想 | 代表算法 | 特点 |
|---|---|---|---|
| 基于值函数的方法 | 通过逼近状态或状态-动作的价值函数(Value Function),间接推导最优策略。 | DQN、Double DQN、Dueling DQN、Rainbow | 适用于离散动作空间,依赖贝尔曼方程更新。 |
| 基于策略梯度的方法 | 直接参数化策略并优化策略参数,通过梯度上升最大化长期回报。 | REINFORCE、PPO、TRPO、DDPG(确定性策略梯度) | 支持连续动作空间(如机器人控制、自动驾驶),直接优化策略,方差较高但灵活性更强。 |
| Actor-Critic混合方法 | 结合值函数(Critic)和策略(Actor),Critic评估动作价值,Actor优化策略。 | A3C、A2C、SAC、TD3 | 融合值函数和策略梯度,平衡偏差与方差,训练更稳定。 |
| 基于模型的方法 | 学习环境动态模型(Model-Based),利用模型规划或辅助策略优化。 | Dyna-Q、MBPO、PETS、MuZero | 样本效率高,但对模型精度敏感;适合真实环境交互成本高的场景。 |
| 其他扩展方法 | 针对复杂问题的改进框架(分层、多智能体、元学习等)。 | HRL(分层强化学习)、MA-DRL(多智能体DRL)、Meta-RL | 解决稀疏奖励、多任务学习、多智能体协作等挑战。 |
这里先列出一个大致的框架,由于具体的使用我也是在之后边学习边总结的,所以详细介绍放在每个小章节里吧。
二、问题设计

假设有一个3×3的迷宫(如上图),用S表示起点(入口)、E表示终点(出口)、O表示通路、W表示墙壁,目标是从S到E找到一条通路。
三、[基于价值的普通强化学习]Q-learning
1 原理
Q-learning是一种基于值函数的强化学习方法,其核心思想是通过更新和维护动作值函数
Q
(
s
,
a
)
Q(s,a)
Q(s,a)来间接推导出最优策略,使用Q-table存储每个状态-动作对的期望奖励。与深度学习中的反向传播不同,Q-learning在传统实现中并不依赖反向传播。
Q
(
s
,
a
)
Q(s,a)
Q(s,a)的更新公式为贝尔曼方程:
Q
(
s
,
a
)
←
Q
(
s
,
a
)
+
α
[
r
+
γ
max
a
′
Q
(
s
′
,
a
′
)
−
Q
(
s
,
a
)
]
Q(s,a)←Q(s,a)+α[r+γ\max_{a'}Q(s',a')-Q(s,a)]
Q(s,a)←Q(s,a)+α[r+γa′maxQ(s′,a′)−Q(s,a)]
其中,
α
α
α是学习率,
γ
γ
γ是折扣因子,
r
r
r是当前奖励,
s
′
s'
s′是下一个状态。这是一个迭代更新公式,直接对Q-table进行更新,无需显式的梯度计算或反向传播,Q-table存储了所有状态-动作对的值,更新过程是逐个元素地调整表格中的值。
2 模拟
(一) 参数设计
- 奖励规则:到达终点奖励+100;到达墙壁或超出迷宫奖励-10;其他情况奖励分值为6-到出口最短路线距离(假设这些距离提前都计算好了)。比如走到(1,0)+3,走到(2,2)+4,走到(0,1)-10,走到(0,2)+100。
- 贝尔曼方程参数: α = 0.8 α=0.8 α=0.8; γ = 0.2 γ=0.2 γ=0.2。
(二)Q-table初始化
初始化一个Q-table,大小为状态数×行为数。对于3×3的迷宫,状态数为9(每个格子为一个状态),行为数为4(上下左右)。初始化Q-table为0:

(三)学习过程
(1) 第一次
状态和状态转移:
| 状态s | 行为(随机) | 下一个状态s’ |
|---|---|---|
| (0,0) | UP | × |
更新Q-table:
| 原始Q[(0,0), UP] | 奖励 | 下一状态能获得的最大奖励 | 更新后的Q[(0,0), UP] |
|---|---|---|---|
| 0 | -10 | 0 | -8 |
结果:

(2) 第二次
状态和状态转移:
| 状态s | 行为(随机) | 下一个状态s’ |
|---|---|---|
| (0,0) | DOWN | (1,0) |
更新Q-table:
| 原始Q[(0,0), DOWN] | 奖励 | 下一状态能获得的最大奖励 | 更新后的Q[(0,0), DOWN] |
|---|---|---|---|
| 0 | +3 | 0 | 2.4 |
结果:

(3) 第三次
| 状态s | 行为(随机) | 下一个状态s’ | 原始Q[(1,0), RIGHT] | 奖励 | 下一状态能获得的最大奖励 | 更新后的Q[(1,0), RIGHT] |
|---|---|---|---|---|---|---|
| (1,0) | RIGHT | (1,1) | 0 | +4 | 0 | 3.2 |
结果:

(4) 中间省略1000次
| 状态s | 行为(随机) | 下一个状态s’ | 原始Q[(1,1), LEFT] | 奖励 | 下一状态能获得的最大奖励 | 更新后的Q[(1,1), LEFT] |
|---|---|---|---|---|---|---|
| (1,1) | LEFT | (1,0) | 0 | +3 | 3.2 | 2.912 |
| 状态s | 行为(随机) | 下一个状态s’ | 原始Q[(1,0), DOWN] | 奖励 | 下一状态能获得的最大奖励 | 更新后的Q[(1,0), DOWN] |
|---|---|---|---|---|---|---|
| (1,0) | DOWN | (2,0) | 0 | +2 | 0 | 1.6 |
自己抽签和计算太麻烦了,于是写了代码大致模拟了一下。
# Dangerous
import random
keys = [(0,0,'up'), (0,0,'down'), (0,0,'left'), (0,0,'right'),
(0,1,'up'), (0,1,'down'), (0,1,'left'), (0,1,'right'),
(0,2,'up'), (0,2,'down'), (0,2,'left'), (0,2,'right'),
(1,0,'up'), (1,0,'down'), (1,0,'left'), (1,0,'right'),
(1,1,'up'), (1,1,'down'), (1,1,'left'), (1,1,'right'),
(1,2,'up'), (1,2,'down'), (1,2,'left'), (1,2,'right'),
(2,0,'up'), (2,0,'down'), (2,0,'left'), (2,0,'right'),
(2,1,'up'), (2,1,'down'), (2,1,'left'), (2,1,'right'),
(2,2,'up'), (2,2,'down'), (2,2,'left'), (2,2,'right')]
values = [-8,2.4,0,0,0,0,0,0,0,0,0,0,0,0,0,3.2,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] # 经历三次学习后的值
rewards = [[2, -10, 100], [3, 4, 5], [2, -10, 4]]
action_list = ['up', 'down', 'left', 'right']
qTable = dict(zip(keys, values)) # 创建初始列表
alpha = 0.8
gamma = 0.2
now_x = 1
now_y = 1
def transfer_x(x, act):
if act == 'up': return x-1
elif act == 'down': return x+1
else: return x
def transfer_y(y, act):
if act == 'left': return y-1
elif act == 'right': return y+1
else: return y
for i in range(1000): # 学习1000次
action = random.choice(action_list) # 行为
next_x = transfer_x(now_x, action) # 下一个状态s'
next_y = transfer_y(now_y, action)
before_q = qTable[(now_x, now_y, action)] # 原始Q
if next_x not in [0,1,2] or next_y not in [0,1,2]: # 奖励
reward = -10
else: reward = rewards[next_x][next_y]
if next_x not in [0, 1, 2] or next_y not in [0, 1, 2]: # 下一状态能获得的最大奖励
max_reward = 0
else:
max_reward = 0
for a in action_list:
r = qTable[(next_x, next_y, a)]
if r > max_reward: max_reward = r
qTable[(now_x, now_y, action)] = before_q + alpha * (reward + gamma * max_reward - before_q) # 更新后的Q值
random_start_list = [(0,0), (1,0), (1,1), (1,2), (2,0), (2,2)]
random_start = random.choice(random_start_list)
random_p = random.randint(1,10)
random_flag = True if random_p == 1 else False
if next_x == 0 and next_y == 2: # 如果走到终点就从随机位置开始
now_x = random_start[0]
now_y = random_start[1]
elif next_x not in [0, 1, 2] or next_y not in [0, 1, 2]:
# 如果走出去就不改变当前位置(以0.1的概率随机初始位置)
if random_flag:
now_x = random_start[0]
now_y = random_start[1]
elif next_y == 1 and (next_x == 0 or next_x == 2):
# 如果走到墙上就不改变当前位置(以0.1的概率随机初始位置)
if random_flag:
now_x = random_start[0]
now_y = random_start[1]
else: # 或者以0.1的概率随机初始位置
now_x = next_x
now_y = next_y
if random_flag:
now_x = random_start[0]
now_y = random_start[1]
# 打印Q表
for key in qTable:
print("key:" + str(key) + " " + str(qTable[key]))
(四)结果
得到结果如下:

其中阴影部分是墙和终点的位置,由于无法到达墙、到达终点后游戏结束,所以这两个位置不会更新Q值。
上表的解释:在(0,0)位置时(对应当前状态),Q值在行为"down"处最大为4.8,因此应该向下走,下一个状态是(1,0)。其余位置类似。

红色箭头表示每一个状态的最优行为,绿色箭头表示用该方法计算得出的最优路线。
四、[基于价值的深度强化学习]DQN
DQN和Q学习的主要区别在于如何表示和更新Q值,DQN使用神经网络来近似Q值函数,而不是使用表格。
1 经验回放
经验回放(Experience Replay)是强化学习中的一个重要技术,主要用于解决强化学习算法中的一些问题,提高算法的稳定性和学习效率。

具体来说,就是不每次都立刻进行Q值计算和反向传播,而是将每次的<状态、动作、状态转移>(称为经验样本或经验元组)先放到缓冲区,然后每次从缓冲区取一部分一次性计算。类似计算机视觉中同时对数据集中的多张图片进行处理,大小表示为batch_size。
2 原理
其实就是将Q学习中需要查Q-table的时候都用网络替换。旧的Q表值和奖励共同作用下更新为新的Q表值。
(我以前一直以为是要让Q值越来越拟合奖励,所以很奇怪,明明奖励的公式我们已经知道了,还要怎么去学习呢,其实奖励只是作为一个已知的数值加入到计算中,并不是说我们要去模拟奖励的生成方式。)
Q-learning中的贝尔曼方程:
Q
(
s
,
a
)
←
Q
(
s
,
a
)
+
α
[
r
+
γ
max
a
′
Q
(
s
′
,
a
′
)
−
Q
(
s
,
a
)
]
Q(s,a)←Q(s,a)+α[r+γ\max_{a'}Q(s',a')-Q(s,a)]
Q(s,a)←Q(s,a)+α[r+γa′maxQ(s′,a′)−Q(s,a)]
可以写为:
Q
(
s
,
a
)
←
(
1
−
α
)
Q
(
s
,
a
)
+
α
[
r
+
γ
max
a
′
Q
(
s
′
,
a
′
)
]
Q(s,a)←(1-α)Q(s,a)+α[r+γ\max_{a'}Q(s',a')]
Q(s,a)←(1−α)Q(s,a)+α[r+γa′maxQ(s′,a′)]
就像加权求和,它在原来Q的基础上加上了一部分奖励作用下的分数。
深度Q-learning中的损失函数:
L
(
θ
)
=
E
s
,
a
,
r
,
s
′
[
(
Q
θ
(
s
,
a
)
−
(
r
+
γ
max
a
′
Q
θ
−
(
s
′
,
a
′
)
)
)
2
]
L(θ)=\mathbb{E}_{s,a,r,s'}[(Q_θ(s,a)-(r+γ\max_{a'}Q_{θ^-}(s',a')))^2]
L(θ)=Es,a,r,s′[(Qθ(s,a)−(r+γa′maxQθ−(s′,a′)))2]
它就是使计算得到的Q值逐渐趋于稳定,基本上等于那个奖励作用下的分数,这个分数不仅考虑了当前奖励,还考虑了下一步能够得到的分数。注意上式中有两组参数,分别为 θ θ θ和 θ − θ^- θ−,对应两个网络(结构一样)。
-
Q
θ
(
s
,
a
)
Q_θ(s,a)
Qθ(s,a)通过主网络训练得到
主网络(Main Network)也称为在线网络(Online Network)或当前网络(Current Network)。主网络负责学习环境中的状态-动作值函数(Q函数),即预测在给定状态下采取某个动作所能获得的预期回报。主网络通过梯度下降等优化算法不断更新其参数,以最小化预测Q值和实际Q值之间的差距。主网络直接与环境交互,根据采集到的经验(状态、动作、奖励、下一个状态)进行学习。 -
max
a
′
Q
θ
−
(
s
′
,
a
′
)
\max_{a'}Q_{θ^-}(s',a')
maxa′Qθ−(s′,a′)由目标网络计算
目标网络(Target Network)是主网络的一个延迟更新版本,其参数定期从主网络复制过来。目标网络不直接参与学习,而是为主网络提供一个稳定的训练目标。在计算Q值的目标值时,使用目标网络来预测下一个状态下的Q值,这样可以减少学习过程中的方差,使学习更加稳定。目标网络的更新频率通常低于主网络,例如,每几千个时间步更新一次。
说明通过神经网络得到的Q值不仅体现了当前决策的奖励,还综合了未来的奖励。
3 模拟
(一)参数设计
- 奖励规则:到达终点奖励+1000;到达墙壁或超出迷宫奖励-1000;其他情况奖励分值不等(假设这些距离提前都计算好了),迷宫格内的奖励矩阵可以表示为:
R = [ 5 − 1000 1000 50 200 500 5 − 1000 200 ] R=\begin{bmatrix} 5&-1000&1000 \\ 50&200&500 \\ 5&-1000&200 \end{bmatrix} R= 5505−1000200−10001000500200 - 损失函数贝尔曼方程参数: γ = 0.4 γ=0.4 γ=0.4。
- 网络输入:状态
s
s
s,由坐标表示(长度为2的列表)。从上往下三行的行号分别为0、1、2,从左到右三列的列标号分别为0,1,2,
(0,0)是起点位于左上角,(0,2)是终点位于右上角。 - 网络输出:每个动作的Q值(长度为4的列表)。
- 隐藏层架构:1层有16个神经元的全连接层,激活函数为ReLU。
- 梯度学习率:0.01。
- ε-贪婪策略:初始阶段,以较高概率ϵ(设置为1.0)随机选择动作。随着训练进行,逐渐降低ϵ(最后衰减到0.25),更多地依赖网络预测的动作。衰减速度为0.995。
- 经验回放:缓冲区大小为 100 100 100, b a t c h s i z e = 32 batch_{size}=32 batchsize=32。
- 同步目标网络步长为100。
10.训练次数:1000
(二)学习过程
- 初始化将智能体放置在起点
(0,0)。 - 选择动作。使用ε-贪婪策略选择动作a。如果 r a n d o m < ϵ random<ϵ random<ϵ,随机选择动作。否则,选择 a r g max a Q θ ( s , a ) arg\max_aQ_θ(s,a) argmaxaQθ(s,a)。
- 执行动作:根据选定的动作 a a a,更新智能体的位置 s ′ s′ s′。如果超出迷宫范围或撞到障碍墙,给予奖励-1000;如果到达终点 (0, 2),给予奖励 1000 并结束回合;否则,根据奖励矩阵 R R R给出奖励 r r r并继续选择下一步动作。
- 存储经验:将经验存入缓冲区。
- 采样并更新网络:从缓冲区中随机采样一批数据计算目标值。
更新主网络参数 θ θ θ以最小化损失函数 L ( θ ) L(θ) L(θ)。 - 同步目标网络:每隔若干步,将主网络参数复制到目标网络。
- 测试(关闭探索,使用网络预测的动作观察智能体是否能够成功从起点走到终点)。
# Dangerous
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import random
def plus1(state): # 原来以为输入是0有可能会在乘法计算的时候使参数不生效,所以统一加了1,后来发现不加1效果更好,可见没必要考虑是否非0
# return [x+1 for x in state]
return state
class DQNAgent:
def __init__(self, state_size, action_size):
self.state_size = state_size # 状态向量大小=2(x坐标和y坐标)
self.action_size = action_size # 动作向量大小=4
self.memory = [] # 经验缓冲区
self.memory_size = 100
self.gamma = 0.4 # 折扣因子
self.epsilon = 1.0 # 初始ε
self.epsilon_min = 0.25 # ε衰减下限
self.epsilon_decay = 0.995 # ε衰减率
self.learning_rate = 0.01 # 学习率α
self.model, self.optimizer = self._build_model() # 主网络
self.target_model, self.optimizer_bed = self._build_model() # 目标网络
self.update_target_model() # 同步网络参数
def _build_model(self):
class NeuralNetwork(nn.Module):
def __init__(self, input_dim, output_dim):
super(NeuralNetwork, self).__init__()
# 隐藏层大小为16
self.fc1 = nn.Linear(input_dim, 16)
self.fc2 = nn.Linear(16, output_dim)
def forward(self, x):
x = torch.relu(self.fc1(x))
return self.fc2(x)
model = NeuralNetwork(self.state_size, self.action_size)
optimizer = optim.Adam(model.parameters(), lr=self.learning_rate)
return model, optimizer
def update_target_model(self):
# Copy weights from the main model to the target model
self.target_model.load_state_dict(self.model.state_dict())
def remember(self, state, action, reward, next_state, done):
if len(self.memory) >= self.memory_size:
self.memory.pop(0)
self.memory.append((state, action, reward, next_state, done))
def act(self, state): # 已知状态
# 要么随机选择动作
if np.random.rand() <= self.epsilon:
return random.choice(range(self.action_size))
# 要么选择下一个最有可能的动作
state = torch.tensor(plus1(state), dtype=torch.float32).unsqueeze(0) # 在0维插入一个维度 # plus1(state)
q_values = self.model(state).detach().numpy() # 计算Q值
return np.argmax(q_values[0])
"""
.unsqueeze()插入维度
大多数深度学习框架(包括 PyTorch)中的神经网络模型期望输入数据具有特定的形状。对于全连接网络,输入通常需要是二维张量,形状为
(batch_size, input_dim):
batch_size:表示批量大小,即一次输入的数据样本数量。
input_dim:表示每个样本的特征维度。
例如,如果 state 是 [0, 0],它的原始形状是 (2,),表示一个一维数组。但神经网络期望输入的是 (1, 2),
其中 1 表示批量大小(只有 1 个样本),2 表示状态的特征维度。
"""
"""
.detach() 方法会创建一个新的张量,与原张量共享数据但不记录梯度信息。也就是说,使用 .detach() 后的张量不再参与反向传播计算。
"""
def replay(self, batch_size):
if len(self.memory) < batch_size:
return # 前31个经验样本只生成不训练
minibatch = random.sample(self.memory, batch_size) # 从memory中随机抽取batch_size个样本
for state, action, reward, next_state, done in minibatch:
state = torch.tensor(plus1(state), dtype=torch.float32).unsqueeze(0) # plus1(state)
next_state = torch.tensor(plus1(next_state), dtype=torch.float32).unsqueeze(0) # plus1(state)
# 计算Q值是奖励值r加未来回报,要判断有没有下一步从而判断加不加回报
target = reward
if not done:
"""torch.max()返回最大值和索引"""
target = reward + self.gamma * torch.max(self.target_model(next_state)).item()
target_f = self.model(state).clone().detach().numpy()[0] # 用主网络计算得到的当前状态的Q值
target_f[action] = target # 更新对应动作下的理想Q值用于计算损失(不更新经验缓冲池)
target_f = torch.tensor(target_f, dtype=torch.float32).unsqueeze(0)
# Compute loss and backpropagate
self.optimizer.zero_grad() # 将所有梯度清零
prediction = self.model(state)
loss = nn.MSELoss()(prediction, target_f) # 计算实际Q值与理想Q值的损失
loss.backward() # 计算梯度
self.optimizer.step() # 根据梯度更新参数
print("\t loss:{}".format(loss))
# Decay epsilon
if self.epsilon > self.epsilon_min:
self.epsilon *= self.epsilon_decay
# Define the environment
def get_reward(state):
x, y = state
rewards = [[5, -1000, 1000], [50, 200, 500], [5, -1000, 200]]
if x < 0 or x >= 3 or y < 0 or y >= 3:
return -1000
return rewards[x][y]
def is_terminal(state):
x, y = state
return (x == 0 and y == 2)
def move(state, action):
x, y = state
if action == 0: # UP
x -= 1
elif action == 1: # DOWN
x += 1
elif action == 2: # LEFT
y -= 1
elif action == 3: # RIGHT
y += 1
return [x, y]
# Train the agent
state_size = 2
action_size = 4
agent = DQNAgent(state_size, action_size)
batch_size = 32
episodes = 1000
for e in range(episodes):
# state_start_list = [[0,0], [1,0], [1,1], [1,2], [2,0], [2,2]]
# state = state_start_list[random.randint(0, len(state_start_list)-1)]
"""本来在想每次都从起点走会不会导致第三行的格子学习次数少,数据证明每次都从起点走才效果更好,可能是因为前几步的可靠性会有利于后面的选择"""
state = [0, 0]
done = False
i = 0
while not done: # 每个epoch走到游戏失败就结束,步长不一定相同
i += 1
action = agent.act(state)
next_state = move(state, action)
reward = get_reward(next_state)
done = is_terminal(next_state) or reward == -1000
agent.remember(state, action, reward, next_state, done)
state = next_state
if len(agent.memory) > batch_size:
agent.replay(batch_size)
if e % 20 == 0: # 同步目标网络步长为50
agent.update_target_model() # Update target network periodically
print(f"Episode {e+1}/{episodes}, epsilon: {agent.epsilon}")
# 测试
print("---------------------训练完成---------------------\n")
for x in [0, 1, 2]:
for y in [0, 1, 2]:
if y == 1 and x != 1:
continue
if x == 0 and y == 2:
continue
state = [x, y]
print(state, ":")
state = torch.tensor(plus1(state), dtype=torch.float32).unsqueeze(0) # 在0维插入一个维度 # plus1(state)
q_values = agent.model(state).detach().numpy() # 计算Q值
action = np.argmax(q_values[0])
action_list = ["up", "down", "left", "right"]
for i in range(4):
print("\t\t", action_list[i], ": ", q_values[0][i])
print("\n---------------------模拟结果---------------------")
state = [0, 0]
done = False
step = 0 # 记录步长
action_time = [0, 0, 0, 0]
while not done:
print("当前位置为:", state)
state_temp = torch.tensor(plus1(state), dtype=torch.float32).unsqueeze(0) # 在0维插入一个维度 # plus1(state)
q_values = agent.model(state_temp).detach().numpy() # 计算Q值
action_old = np.argmax(q_values[0])
print("\t old q_values:", q_values[0])
"""本来把重复路线加到了学习的过程中,想减少‘摆烂’绕圈的情况,但是发现步长并没有作为状态输入,所以这样反而会导致奖励一直在变化而无法学习"""
action_time[action] += 1
q_values[0][action_old] -= action_time[action]*5 # 减少重复路线
action_new = np.argmax(q_values[0]) # 根据新的奖励选择动作
print("\t new q_values:", q_values[0])
action = np.argmax(q_values[0])
next_state = move(state, action)
print("\t执行动作:", action_list[action])
print("\t下一位置为:", next_state)
reward = get_reward(next_state)
done = is_terminal(next_state) or reward == -1000
if done:
print("**********停止**********, terminal? ", is_terminal(next_state), " reward=-400: ", reward==-400)
if is_terminal(next_state):
print("到达终点")
state = next_state
print("---------------------模拟结束---------------------")

(三)结果
每个位置上动作的Q值如下:

一次推理的结果如下:

所得结果与Q-learning相同,图示为:

红色箭头表示每一个状态的最优行为,绿色箭头表示用该方法计算得出的最优路线。
五、[基于策略的深度强化学习]REINFORCE
1 区分策略梯度和DQN

某论文中同时提到了策略梯度法和DQN,于是我一直搞不懂二者的联系和区别(也是写本文的主要原因),但是经过进一步了解发现策略梯度算法(Policy Gradient)和深度 Q 网络(DQN)都属于强化学习领域的重要算法,不是两个平行的概念。它们之间的关联已补充总结在文章开始的知识框架中。 下面比较了策略梯度法和基于价值的方法(以DQN为例)。
相同之处
- 联系目标相同:策略梯度算法和 DQN 的目标都是让智能体(agent)在与环境的交互过程中学习到最优策略,以最大化长期累积奖励。
- 都基于经验进行学习:策略梯度算法和 DQN 都依赖于智能体与环境交互产生的经验来更新模型参数。在策略梯度算法中,智能体根据当前策略与环境交互,收集一系列状态、动作和奖励信息,然后利用这些经验来计算策略梯度,更新策略网络的参数。DQN 则将每次交互得到的经验(状态、动作、奖励、下一个状态)存储在经验回放缓冲区中,随机采样经验来训练 Q 网络,从而学习到更好的动作价值估计。
区别
- 学习的对象不同:
策略梯度算法: 直接学习的是策略函数 π θ ( a ∣ s ) \pi_{\theta}(a|s) πθ(a∣s),即智能体如何根据环境状态选择动作,根据当前状态 s s s和网络参数 θ \theta θ输出采取动作 a a a的概率分布。它通过调整策略网络的参数 θ \theta θ,使得智能体采取的动作能够最大化长期奖励。例如,在一个机器人行走的任务中,策略梯度算法会学习一个策略,使得机器人能够根据当前的地形和自身状态选择合适的步伐和动作,以保持平衡并向前移动。
DQN: 学习的是动作价值函数 Q ( s , a ) Q(s, a) Q(s,a),它评估的是在给定状态 s s s下采取动作 a a a的好坏程度。智能体通过学习Q值来间接确定最优策略,即选择具有最大Q值的动作,评估在状态 s 下采取动作 a 所能获得的期望奖励。比如在玩围棋游戏时,DQN 会学习每个局面(状态)下各种落子动作(动作)的价值,然后选择价值最高的落子位置。 - 动作选择方式不同:
策略梯度算法: 根据策略函数输出的动作概率分布来随机选择动作。这种方式允许智能体进行探索,有可能发现一些之前未尝试过但可能带来更高奖励的动作。例如,在一个多臂老虎机问题中,策略梯度算法会根据每个臂的选择概率来随机选择臂,以探索不同臂的奖励情况。
DQN: 基于动作价值函数,选择具有最大 Q 值的动作(通常采用贪心策略)。这种方式在一定程度上更倾向于选择已知的最优动作,探索性相对较弱。不过,为了增加探索性,DQN 通常会采用ϵ- 贪心策略,即有一定概率ϵ随机选择动作,而不是总是选择具有最大Q值的动作。 - 训练稳定性不同:
策略梯度算法: 训练过程相对不稳定,因为策略梯度的估计存在一定的方差。在更新策略网络参数时,由于每次采样得到的经验不同,计算出的策略梯度可能会有较大波动,导致训练过程不易收敛。
DQN: 通过经验回放和目标网络等技术,在一定程度上提高了训练的稳定性。经验回放打破了数据之间的时间相关性,使得训练数据更加独立同分布;目标网络则减少了目标值的变化频率,降低了训练的不稳定性。
也就是说之前的公式可能表示的有些问题,在DQN中并没有用到参数 θ \theta θ,我们更新的参数只是神经网络的参数,并不是策略函数的参数。但是我其实还是没有理解,除了输出是概率而不是Q值,看起来明明训练的都是一个策略网络。
策略梯度方法执行的是非确定性策略。
非确定性策略:在每种状态下,执行的动作是随机的,可以按照概率值选择动作(如Softmax输出执行每个动作的概率)。
确定性策略:在某种状态下,要执行的动作是唯一且确定的。
2 原理
REINFORCE算法也被称为蒙特卡罗策略梯度算法。智能体的策略由一个参数化的策略函数
π
θ
(
a
∣
s
)
\pi_{\theta}(a|s)
πθ(a∣s)表示,该函数输出在状态
s
s
s下采取动作
a
a
a的概率。
REINFORCE算法的目标是最大化智能体的长期累计奖励,具体来说就是要找到一组最优的参数
θ
\theta
θ使得期望累计
J
(
θ
)
J(\theta)
J(θ)最大,期望累计奖励可以表示为:
J
(
θ
)
=
E
π
θ
[
∑
t
=
0
T
r
t
]
J(\theta)=\mathbb{E}_{\pi_\theta}[\sum^{T}_{t=0}r_t]
J(θ)=Eπθ[t=0∑Trt]
其中,
T
T
T是整个episode(从起始状态到终止状态的一个完整过程)的时间长度。
为了找到使目标函数
J
(
θ
)
J(\theta)
J(θ)最大化的参数
θ
\theta
θ,需要计算目标函数关于参数
θ
\theta
θ的梯度,即策略梯度
∇
θ
J
(
θ
)
∇_θJ(θ)
∇θJ(θ)。根据策略梯度定理,策略梯度可以表示为下式(详情可见【机器学习】强化学习(3)——深度强化学习的数学知识)。
∇
θ
J
(
θ
)
=
E
π
θ
[
∑
t
=
0
T
∇
θ
log
π
θ
(
a
t
∣
s
t
)
⋅
G
t
]
∇_θJ(\theta)=\mathbb{E}_{\pi_\theta}[\sum^{T}_{t=0}∇_θ\log_{}\pi_\theta(a_t|s_t)·G_t]
∇θJ(θ)=Eπθ[t=0∑T∇θlogπθ(at∣st)⋅Gt]
其中,
a
t
a_t
at和
s
t
s_t
st分布是在时间步
t
t
t采取的动作和所处的状态,
G
t
=
∑
k
=
t
T
γ
k
−
t
r
k
G_t=\sum^T_{k=t}\gamma^{k-t}r_k
Gt=∑k=tTγk−trk是从时间步
t
t
t开始的累计折扣奖励,
log
π
θ
(
a
t
∣
s
t
)
\log_{}\pi_\theta(a_t|s_t)
logπθ(at∣st)是对数策略函数(对于离散动作空间,策略函数给出的是在状态
s
s
s下采取每个离散动作
a
a
a的概率,对于连续动作空间,策略函数是概率密度,对数策略函数是对策略函数取自然对数)。
其实了解完策略梯度的原理后,我还是有些不清楚二者本质的区别。
- Q:是已知“期望路径”来训练策略使得期望路径作为概率最大的动作被选择吗?
A: 在实际应用中,智能体按照当前策略与环境进行交互,采样得到多个轨迹(trajectory,即状态、动作、奖励的序列)。通过这些采样得到的轨迹来近似计算策略梯度中的期望。这个过程中,智能体并不知道所谓的 “期望路径” 是什么,只是不断地探索环境,根据采样得到的数据来调整策略,使得策略逐渐优化,最终找到一个能够获得较高累计奖励的策略。策略梯度方法鼓励智能体进行探索,因为策略是基于概率分布来选择动作的。这种探索行为有助于发现不同的路径和可能获得高奖励的动作组合。如果事先知道期望的路径,反而限制了智能体的探索能力,不利于找到真正的最优策略。策略梯度方法通过不断地根据采样数据更新策略,逐步逼近最优策略,而不是依赖于已知的期望路径。 - Q:REINFORCE的损失函数是什么?如何理解它的目标?
A:它没有传统意义上像监督学习那样明确的损失函数,它的目标是最大化期望累计奖励 J ( θ ) J(\theta) J(θ)。用通俗的语言解释策略梯度, ∇ θ log π θ ( a t ∣ s t ) ∇_θ\log_{}\pi_\theta(a_t|s_t) ∇θlogπθ(at∣st)反映了参数 θ \theta θ的微小变化对在状态 s t s_t st下采取动作 a t a_t at的概率的影响,通过调整参数,让采取动作的概率增加或减少,从而扩大收益或减小损失,最后达到稳定(即好的动作轨迹概率高,不好的轨迹概率低)。因为概率 p p p总是小于1,所以 log p \log p logp总是负数,且随着 p p p的增大而增大(绝对值减小),当 G G G为正时(好的反馈),说明应该增大动作的概率从而扩大奖励,由于 log p \log p logp是负的,所以 J J J是负的,要让绝对值减小(因为目标是使 J J J最大),即让 log p \log p logp增大,也就是让 p p p增大了;当 G G G为负时(坏的反馈),说明应该减少动作的概率从而减少损失,由于 log p \log p logp是负的,所以 J J J是正的,要让绝对值增大(因为目标是使 J J J最大),即让 log p \log p logp减小,也就是让 p p p减小了。
其实这么看,基于策略的学习,有点像在学习DQN中的“ϵ- 贪心策略”,只不过在DQN中是指定使用ϵ- 贪心,而我们通过学习来自己设计一个选择动作的方式,这个方式能够使我们大概率获得大的收益。那么我猜想,将DQN中的ϵ- 贪心换成我们的策略网络,可能就是Actor-Critic算法的效果。
策略概率反映的是当前策略的动作偏好,而Q值代表的是动作的真实长期价值。 基于价值的方法和基于策略的方法,最后的结果可能是一致的(动作概率高的价值也高),但是在训练的不同阶段可能出现不匹配,因为策略可能尚未学习到最优动作,导致存在动作概率高的动作实际上Q值可能并不高的问题。所以其实我认为二者没有什么本质的区别,一个是以固定的学习方式找到答案,另一个是通过不断优化学习方式能够马上找到答案。
(一)参数设计
- 奖励规则:到达终点奖励+1000;到达墙壁或超出迷宫奖励-1000;其他情况奖励分值不等(假设这些距离提前都计算好了),迷宫格内的奖励矩阵可以表示为:
R = [ 5 − 1000 1000 50 200 500 5 − 1000 200 ] R=\begin{bmatrix} 5&-1000&1000 \\ 50&200&500 \\ 5&-1000&200 \end{bmatrix} R= 5505−1000200−10001000500200 - 折扣因子: γ = 0.8 γ=0.8 γ=0.8。
- 网络输入:状态
s
s
s,由坐标表示(长度为2的列表)。从上往下三行的行号分别为0、1、2,从左到右三列的列标号分别为0,1,2,
(0,0)是起点位于左上角,(0,2)是终点位于右上角。 - 网络输出:通过softmax输出每个动作的概率(长度为4的列表)。
- 隐藏层架构:1层有16个神经元的全连接层,激活函数为ReLU。
- 梯度学习率:0.01。
- 训练次数:1000
(二)学习过程
- 初始化将智能体放置在起点
(0,0)。 - 选择动作。使用策略网络选择动作a。
- 执行动作:根据选定的动作 a a a,更新智能体的位置 s ′ s′ s′。如果超出迷宫范围或撞到障碍墙,给予奖励-1000;如果到达终点 (0, 2),给予奖励 1000 并结束回合;否则,根据奖励矩阵 R R R给出奖励 r r r并继续选择下一步动作。
- 更新网络:更新网络参数 θ θ θ以最小化损失函数 J ( θ ) J(θ) J(θ)。
- 测试(关闭探索,使用网络预测的动作观察智能体是否能够成功从起点走到终点)。
# Dangerous
import torch
import torch.nn as nn
import torch.optim as optim
# 定义迷宫环境
class MazeEnv:
def __init__(self):
self.state = (0, 0)
self.rewards = [[5, -1000, 1000], [50, 200, 500], [5, -1000, 200]]
self.done = False
def reset(self):
self.state = (0, 0)
self.done = False
return self.state
def step(self, action):
x, y = self.state
flag = True # 标记是否需要惩罚
if action == 0: # 上
if x - 1 < 0:
flag = False
x = max(x - 1, 0)
elif action == 1: # 下
if x + 1 > 2:
flag = False
x = min(x + 1, 2)
elif action == 2: # 左
if y - 1 < 0:
flag = False
y = max(y - 1, 0)
elif action == 3: # 右
if y + 1 > 2:
flag = False
y = min(y + 1, 2)
if (x, y) in [(0, 1), (2, 1)]:
pass # 遇到障碍物,保持原地
else:
self.state = (x, y)
reward = self.rewards[x][y]
if flag == False:
reward = -1000
if (x, y) == (0, 2):
self.done = True
return self.state, reward, self.done
# 定义策略网络
class PolicyNetwork(nn.Module):
def __init__(self, state_size, action_size):
super(PolicyNetwork, self).__init__()
self.fc = nn.Linear(state_size, 16)
self.action_head = nn.Linear(16, action_size)
def forward(self, x):
x = torch.relu(self.fc(x))
action_prob = torch.softmax(self.action_head(x), dim=-1)
'''
dim 参数指定了 Softmax 操作的维度。dim=-1 表示对输入张量的最后一个维度应用 Softmax 函数。
'''
return action_prob
# 初始化环境、网络和优化器
env = MazeEnv()
state_size = 2
action_size = 4
policy_net = PolicyNetwork(state_size, action_size)
optimizer = optim.Adam(policy_net.parameters(), lr=0.01)
# 训练循环
num_episodes = 1000
gamma = 0.8
for episode in range(num_episodes):
state = env.reset()
log_probs = []
rewards = []
while not env.done and len(log_probs)<=10: # 防止数组长度太大导致OOM
state_tensor = torch.FloatTensor(state).unsqueeze(0) # s
action_probs = policy_net(state_tensor) # a_p_list
action_dist = torch.distributions.Categorical(action_probs)
action = action_dist.sample() # a
log_prob = action_dist.log_prob(action) # a_logP
""" torch.distributions.Categorical
是 PyTorch 中的一个类,用于表示分类分布(Categorical Distribution)。用于建模从一组有限类别中选择一个类别的过程。
<action_probs>表示每个类别的相对概率。这些概率会被归一化,使得它们的和为 1。
sample():从分布中抽取一个样本。返回的样本是一个整数,表示被选中的类别
log_prob(value):计算给定值的对数概率
"""
next_state, reward, done = env.step(action.item())
log_probs.append(log_prob)
rewards.append(reward)
state = next_state
discounts = [gamma ** i for i in range(len(rewards) + 1)]
R = sum([a * b for a, b in zip(discounts, rewards)]) # G_t
if not env.done: # 这是对游戏失败的惩罚
R = R - len(log_probs)*len(log_probs)*1000
policy_loss = []
for log_prob in log_probs: # 最大化J等于最小化-J
policy_loss.append(-log_prob * R)
optimizer.zero_grad()
policy_loss = torch.cat(policy_loss).sum()
""" torch.cat(policy_loss).sum()
torch.cat(policy_loss):将 policy_loss 列表中的所有标量损失值合并成一个一维张量。
.sum():计算这些损失值的总和,以便我们可以基于这个总损失来更新模型参数。
"""
policy_loss.backward()
""" policy_loss.backward()
在PyTorch中,当你对张量执行任何运算(例如加法、乘法等)时,这些操作会被记录在一个计算图(computation graph)中。
这意味着所有的操作及其输入都会被追踪,以便后续能够进行自动微分和反向传播。
每个操作都被视为一个节点,输入和输出张量作为边。
当调用 .backward() 方法时,PyTorch会从损失开始沿着计算图逆向遍历,计算每个参数的梯度。
只有当张量的 requires_grad 属性设置为 True 时,对该张量执行的操作才会被记录在计算图中。
"""
optimizer.step()
if episode % 1 == 0:
print(f"Episode {episode}/{num_episodes}, Reward: {sum(rewards)}")
# 测试
print("---------------------训练完成---------------------\n")
for x in [0, 1, 2]:
for y in [0, 1, 2]:
if y == 1 and x != 1:
continue
if x == 0 and y == 2:
continue
state = [x, y]
print_list = []
print_list.append(state)
state_tensor = torch.FloatTensor(state).unsqueeze(0) # s
action_probs = policy_net(state_tensor) # a_p_list
action_list = ["up", "down", "left", "right"]
for i in range(4):
s1 = action_list[i]
s2 = ":"
s3 = str(round(action_probs[0][i].item(), 5))
s = s1 + s2 + s3
print_list.append(s)
print(print_list)
print("\n---------------------模拟结果---------------------")
state = env.reset()
i = 0
while not env.done:
print("当前位置为:", state)
state_tensor = torch.FloatTensor(state).unsqueeze(0) # s
action_probs = policy_net(state_tensor) # a_p_list
action = torch.argmax(action_probs) # max_a
next_state, reward, done = env.step(action)
print("\t奖励:", reward)
action_list = ['up', 'down', 'left', 'right']
print("\t执行动作:", action_list[action])
print("\t下一位置为:", next_state)
if env.done:
print("到达终点")
state = next_state
i += 1
assert i != 10
print("---------------------模拟结束---------------------")
(三)结果

虽然在(1, 1)处向左走和向右走概率区别不大,但是智能体已经可以顺利走到终点,图示为:

红色箭头表示每一个状态的最优行为,绿色箭头表示用该方法计算得出的最优路线。
在改代码的过程中,我感受到REINFORCE似乎较DQN相比需要的提示较少,不用人为地设置过多奖励和惩罚规则,除了损失函数的设置有点抽象之外,似乎表现更好,用时和结果上都没有较大的缺点。
3 基于策略的普通强化学习
基于价值的强化学习,可以把每个状态下对应的动作的价值存储起来,那么如果不用神经网络,如何表示策略呢?实际上就是每个状态下对应的采取每个动作的概率。
对于状态空间和动作空间较小的问题,可以直接用表格的形式存储每个状态下采取每个动作的概率,这种方法简单直观,但不适用于大规模或连续的状态和动作空间。
与神经网络类似,可以使用线性函数近似的方式,策略被表示为一个参数化的线性组合器,其中的权重是需要学习的参数。或者使用其他类型的非线性模型作为策略函数的近似器,比如决策树、支持向量机等。
六、 [Actor-Critic] PPO
1 演员-评论家算法概述
组成部分
- Actor(演员):本质是一个策略网络,以环境状态 S t S_t St作为输入,输出动作的概率分布 P ( a t ∣ s t ) P(a_t|s_t) P(at∣st),根据这个概率分布来选择动作执行。
- Critic(评论家):是一个价值网络,用于评估Actor采取的动作的好坏。它输入状态 S t S_t St或者状态-动作对 ( s t , a t ) (s_t, a_t) (st,at),输出一个标量值,代表从该状态开始,采取相应动作后能获得的期望累计奖励,即状态动作价值 Q ( s t , a t ) Q(s_t,a_t) Q(st,at)或者状态价值 V ( s t ) V(s_t) V(st)。
工作流程
- 动作选择:Actor 接收环境状态 S t S_t St,根据内部的策略 P ( a t ∣ s t ) P(a_t|s_t) P(at∣st)产生动作 a t a_t at并执行。
- 价值评估:Critic 根据状态 S t S_t St和动作 a t a_t at得出状态动作价值 Q ( s t , a t ) Q(s_t,a_t) Q(st,at)(或者先根据状态估计 V ( s t ) V(s_t) V(st),再结合奖励等信息计算相关价值)。
- 参数更新:
Actor 更新:使用损失函数 l o s s = − l o g P ( a t ∣ s t ) Q ( s t , a t ) loss=-log P(a_t|s_t)Q(s_t,a_t) loss=−logP(at∣st)Q(st,at)来更新参数。这意味着如果某个状态 S t S_t St下对动作 a t a_t at评估的价值越大,Actor 就越要强化选择 a t a_t at的概率;反之则弱化。
Critic 更新:环境执行动作 a t a_t at后会更新状态为 s t + 1 s_{t + 1} st+1,并给出奖励 R t R_t Rt。Critic 使用损失函数 l o s s = ( Q ( s t + 1 , a t + 1 ) + R t − Q ( a t , a t ) ) 2 loss=(Q(s_{t+1},a_{t+1})+R_t-Q(a_t,a_t))^2 loss=(Q(st+1,at+1)+Rt−Q(at,at))2来更新参数,目的是改进自己预估动作价值的能力。 - 持续交互:重复上述过程,让 Actor 和 Critic 不断优化,使得 Actor 能学习到更好的策略,Critic 能做出更准确的评估。
算法总结
| 算法名称 | 简介 | 备注 |
|---|---|---|
| A2C (Advantage Actor-Critic) | 使用优势函数(Advantage)来减少策略梯度估计的方差 | 同步更新Actor和Critic |
| A3C (Asynchronous Advantage Actor-Critic) | 多个工作线程并行收集数据并更新共享的神经网络模型 | A2C的异步版本 |
| DDPG (Deep Deterministic Policy Gradient) | 1. 针对连续动作空间的确定性策略梯度算法 2. 使用目标网络来稳定训练 | |
| TD3 (Twin Delayed DDPG) | 使用两个Critic网络来减少过估计。引入延迟更新和目标策略平滑来提高稳定性 | DDPG的改进版本 |
| SAC (Soft Actor-Critic) | 1. 最大熵强化学习算法,旨在同时优化累积奖励和策略的熵。 2. 使用软更新和自动调谐的温度参数。 | |
| PPO (Proximal Policy Optimization) | 使用近端策略优化技术来限制策略更新的大小,提高训练稳定性 | 可以视为A2C的改进版本 |
| TRPO (Trust Region Policy Optimization) | 使用信任区域方法来限制策略更新,确保更新在安全的范围内 | 比PPO更复杂,但提供了更强的理论保证。 |
| ACKTR (Actor-Critic using Kronecker-Factored Trust Region) | 结合了自然梯度下降和Kronecker因子化的信任区域方法,提高了大规模问题的训练效率。 | |
| IMPALA (Importance Weighted Actor-Learner Architecture) | 使用重要性采样来结合离线学习和在线学习,适用于大规模分布式训练 | |
| MPO (Model Predictive Control with Off-Policy Correction) | 结合模型预测控制和离线策略修正,适用于需要长期规划和控制的任务 | |
| GAE (Generalized Advantage Estimation) | 是一种改进优势函数估计的方法 | 不是独立的算法,常与A2C等算法结合使用 |
2 PPO(近端策略优化算法)
PPO 算法由 OpenAI 在 2017 年提出,是一种有效的策略梯度方法,旨在解决连续动作空间中的控制问题,可视为 A2C算法的特殊形式。
核心思想
传统策略梯度方法存在策略更新不稳定问题,更新幅度过大易偏离优化方向,过小则降低训练效率。PPO 通过限制新策略与旧策略之间的差异,确保模型在探索新知识时不会偏离原来太远,平衡更新幅度,提升训练稳定性。其核心思想源自信任区域策略优化(TRPO),但采用更简单高效的裁剪机制实现类似效果。
算法步骤
- 初始化策略网络和价值网络:策略网络以环境状态作为输入,输出可能动作的概率分布,代表智能体的决策策略;价值网络用于估计处于给定状态的预期累积奖励,减少策略梯度估计的方差,并为学习提供额外信号。
- 收集轨迹数据:让智能体按照当前策略与环境进行交互,在交互过程中,收集每个时间步的状态 s t s_t st、执行的动作 a t a_t at、获得的奖励$r_t$以及下一个状态 s t + 1 s_{t+1} st+1等数据,形成轨迹数据。
- 计算优势估计:优势函数用于衡量在给定状态下采取特定动作相对于平均动作的好坏。计算优势估计有多种方法,常用的是广义优势估计(GAE)。
(1) 计算TD残差: δ t = r t + γ V ( s t + 1 ) − V ( s t ) δ_t = r_t + γV(s_{t+1}) - V(s_t) δt=rt+γV(st+1)−V(st) 。TD残差常被用作优势函数的近似值,其正负决定了策略更新的方向。若 δ > 0 δ > 0 δ>0,说明当前选择的动作比预期更好,策略更新会增加在该状态下选择此动作的概率;若 δ < 0 δ < 0 δ<0,则表示当前动作比预期差,策略更新会降低选择该动作的概率。同时,TD 残差的绝对值大小决定了策略更新的幅度,绝对值越大,表明当前策略与理想策略的偏差越大,需要进行更大幅度的更新 。
(2) 递归计算 GAE: A t G A E = δ t + ( γ λ ) ⋅ A t + 1 G A E A_t^{GAE} = δ_t + (γλ) \cdot A_{t+1}^{GAE} AtGAE=δt+(γλ)⋅At+1GAE, λ λ λ是 GAE 的衰减系数,用于控制长期和短期偏差的平衡。通过 λ λ λ的调节,GAE 可以在单步TD估计(低方差高偏差)和Monte Carlo估计(高方差低偏差)之间找到一个平衡点。
低方差:只依赖即时奖励和一步之后的状态价值估计,数据波动对其影响较小,所以方差低。比如在一个简单的走迷宫游戏中,每走一步就根据下一步的情况更新价值估计,不会受到后续较远步骤复杂情况的干扰,每次估计的波动不大。
高偏差:仅考虑单步信息,忽略了更长远的奖励信息,使得估计结果与真实价值有较大偏差。还是以走迷宫为例,如果终点的奖励很高,但单步 TD 估计只看下一步,就可能低估当前位置的价值。 - 计算替代目标:计算裁剪后的目标函数,该函数是策略的新旧参数和优势估计的函数。假设当前策略 π θ \pi_{\theta} πθ,旧策略 π θ o l d \pi_{\theta_{old}} πθold,在状态 s t s_t st下采取动作 a t a_t at的概率比 r t ( θ ) = π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) r_t(\theta) = \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)} rt(θ)=πθold(at∣st)πθ(at∣st)。替代目标为 L a c t o r = E t ( min ( r t ( θ ) ⋅ A t G A E , clip ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) ⋅ A t G A E ) ) L^{actor} = \mathbb{E}_t \left( \min(r_t(\theta) \cdot A_t^{GAE}, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) \cdot A_t^{GAE}) \right) Lactor=Et(min(rt(θ)⋅AtGAE,clip(rt(θ),1−ϵ,1+ϵ)⋅AtGAE)),其中 ϵ \epsilon ϵ是裁剪参数(如 0.2), clip \text{clip} clip函数将 r t ( θ ) r_t(\theta) rt(θ)裁剪到区间 [ 1 − ϵ , 1 + ϵ ] [1 - \epsilon, 1 + \epsilon] [1−ϵ,1+ϵ]内,避免策略更新幅度过大。
- 优化策略网络:使用随机梯度下降(SGD)或其变体(如 Adam、RMSProp ),根据计算得到的替代目标来更新策略网络的参数,从而最小化替代目标,使得策略得到优化。
- 优化价值网络:使用均方误差(MSE)损失函数 L c r i t i c = E t ( ( R t − V ( s t ) ) 2 ) L^{critic} = \mathbb{E}_t \left( (R_t - V(s_t))^2 \right) Lcritic=Et((Rt−V(st))2),其中 R t R_t Rt是从时间步t开始的实际累积折扣回报, V ( s t ) V(s_t) V(st)是价值网络的估计值,通过最小化该损失函数来更新价值网络的参数,提升价值估计的准确性。
- 重复迭代:不断重复步骤 2 到步骤 6,持续与环境交互收集新数据,更新策略网络和价值网络,直到智能体在环境中的表现达到满意的程度,或者达到预设的迭代次数。
七、总结
- 基于价值的方法,目标是学习一个价值函数,比如状态价值函数或动作价值函数,通过选择价值最大的动作来间接得到策略。其策略是隐式的(比如ϵ-greedy策略)。
- 基于策略的方法通过优化参数来最大化期望累计奖励,策略是显示的,能够直接输出动作概率分布。 收敛性更稳定,适用于动作空间连续或高维、策略需要高度非线性建模的场景。
| 算法类别 | 算法名称 | 提出时间 | 是否深度强化学习 | 经典/主流 | 核心思想 |
|---|---|---|---|---|---|
| 基于价值的方法 | Q-Learning | 1989 | 否 | 经典 | 无模型、off-policy,通过Q表存储状态-动作值,利用Bellman方程迭代更新 |
| SARSA | 1994 | 否 | 经典 | 无模型、on-policy,直接利用当前策略生成的动作序列更新Q值,适合连续控制任务 | |
| DQN | 2013 | 是 | 主流 将Q-Learning与深度神经网络结合,通过经验回放和目标网络解决高维状态空间问题 | ||
| Double DQN | 2015 | 是 | 主流 | 分离动作选择与价值估计,使用两个Q网络减少Q值高估偏差 | |
| Dueling DQN | 2015 | 是 | 主流 | 将Q值分解为状态价值和动作优势函数,提升状态价值估计效率 | |
| 基于策略的方法 | Policy Gradient | 1992 | 否 | 经典 | 直接优化策略网络参数,通过梯度上升最大化累计奖励,适合连续动作空间 |
| A2C | 2016 | 是 | 主流 | Actor-Critic框架,同步更新策略网络(Actor)和价值网络(Critic),引入优势函数减少方差 | |
| A3C | 2016 | 是 | 主流 | A2C的异步版本,多进程并行训练,提升数据利用效率 | |
| PPO | 2017 | 是 | 主流 | 通过近端策略优化(Clipped Surrogate)提升策略更新稳定性,广泛应用于机器人控制等领域 | |
| SAC | 2018 | 是 | 主流 | 结合最大熵原理,在优化策略时引入熵正则项,平衡探索与利用,适合复杂环境 | |
| DDPG | 2015 | 是 | 主流 | Actor-Critic框架,通过确定性策略梯度处理连续动作空间,引入目标网络提升稳定性 |

【欢迎指正】
特别鸣谢:YanJiayi、谷老师
参考来源:
@AIGC
一文搞懂策略梯度



























 15万+
15万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








