回想一下,接触遥感专业也有几个年头了,而现在越来越偏离遥感了,突然想着把自己脑中的遥感知识整理出来。首先想到的便是坐标系和投影,我想这个东西困扰着80%以上的测绘、遥感和GIS领域的从业人员吧,群里经常有人问,我自己曾经也很迷糊,什么大地坐标系啊、地心坐标系啊、高斯投影啊、UTM投影啊,搞得头都大了,可是这玩意又不能不玩,毕竟空间信息是遥感数据的灵魂,如果定位不准影像就只能当风景画看了。好吧,那就啃吧,基础的东西还是要的,经过一番探索,再加上去年专门做过坐标转换一些工作,算是清晰明了些了,在此就把我的一些见解分享给大家,欢迎各位菜鸟和专家前来吐槽。好了,咱们言归正传,开始坐标系探险记。
1、什么是坐标系?
或许很多人心中明白这个概念,却又不甚明白。什么是坐标系?人们描述空间中的一个点或者一个位置,通常会采用坐标这个概念。可是这个坐标该怎么计算呢?它的参考是谁呢?如果中国定义中南海坐标是(1921,1949,2012),美国佬也定义他们白宫的坐标是(1921,1949,2012),哪天黑马说咱们打它中南海一炮吧,那就可能把他自己烤熟。所以必须要建立一个合理的坐标系(⊙﹏⊙b汗~~,这个理由好牵强啊)。
坐标系由原点和坐标轴组成。坐标系种类很多,我们大家在数学中想必都学过笛卡尔坐标系、极坐标系、球面坐标系和柱面坐标系吧,在地学领域,用到最多的是平面坐标系、空间直角坐标系(前两者属于笛卡尔坐标系)和球面坐标系。比如说一个点坐标是(-2850017.472,4690744.523,3237959.973)就是指空间直角坐标,而我们经常看到的Google Earth上的点的坐标(37°20′17″N,112°33′20″E)就是指球面坐标。
测量学上,坐标系怎样定义的呢?地球是一个不规则的类椭球,怎样用严格的数学方式表示它,应该是测绘学家们所追求的高峰。为了表示地球上每一个点的位置,是不是要建立一个统一的世界坐标系呢?建立坐标系是不是要确定坐标原点和坐标轴呢?那怎样建立呢?测量学家们把地球当作一个规则的椭球来处理,这下就好办多了,椭球中心就原点呗,长轴短轴就作为坐标轴,这样一个坐标系就出来了啊。可是有人会问,那这个椭球怎么表示呢?嘛嘛的,我也想问,原来这是科学家们利用天文观测得到的,而且不同的科学家得到的椭球还不一样,比如,一个叫Krasovsky的人搞了个克拉索夫斯基椭球,还有人搞了什么IUGG-1975、WGS-84、GRS80椭球,他们主要特点是长半轴和扁率不同。可是又有人会问(Y的,问题好多啊),搞这么多椭球干嘛,有一个不就行啦。呵呵,我们知道,地球坑坑洼洼的,用严密的椭球来表示肯定有误差,有的国家为了使自己的国家与椭球面吻合(最好大家都站在椭球面上),这样根据各自的情况就定义了不同的参考椭球,比如北京54坐标系就采用了苏联老大哥的克拉索夫斯基椭球。可是问题又来了,怎样才算吻合得好呢?肯定会有人站在椭球面上,有人站在椭球面下,真头疼。此时,测量学家们引入了大地基准面来衡量椭球与大地的吻合度。大地基准面是由大地水准面而来,是指平均海平面延伸到大陆得到的一个封闭曲面。比如,在建立北京54坐标系时,专家们肯定会选择与中国的大地水准面吻合比较好的椭球。此时的椭球称为参考椭球,建立的坐标系称为参心坐标系,我国的北京54和西安80坐标系都是参心坐标系,是一种局部范围的坐标系。然而这种坐标系对于全球定位来说极其不便,误差很大,所以山姆大叔率先针对GPS系统设计了全球大地坐标系WGS-84坐标系统,这时的大地原点不再是参考椭球的中心,而是地球的质心。WGS84椭球体的相关参数和WGS84坐标系的坐标轴指向请参考相关专业书籍。我国现有的国家2000坐标系也是一种全球大地坐标系,其与WGS-84坐标系稍微有点差异。
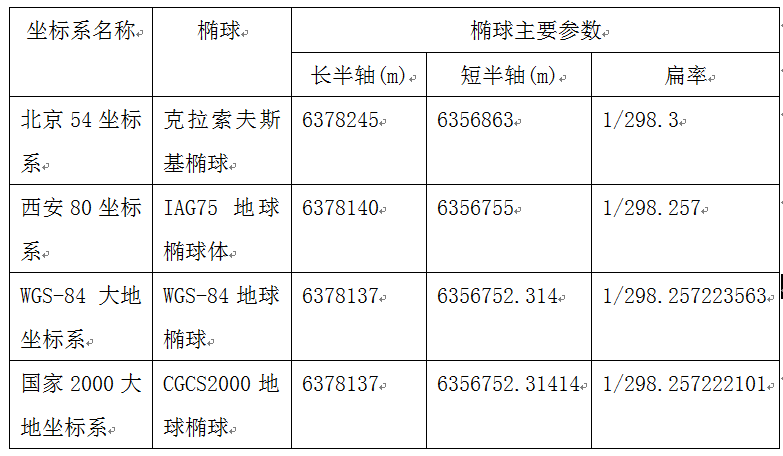
下面是几种常见坐标系的椭球参数:
其中北京54坐标系和西安80坐标系是参心坐标系,而WGS-84坐标系与国家2000坐标系是地心坐标系,坐标原点是地球质心。
好啦,这样大家明白了坐标系的定义了吧,首先,需要定义参考椭球体,有了参考椭球还需要大地基准面(全球大地坐标系就不要了),然后需要定义坐标系原点和坐标轴的指向。这样一个坐标系就建立了,以后找妹子就方便多了,全球定位吧,哈哈!
2、为什么要投影?
大家会想,有了坐标就行了,为什么还要搞个让人迷糊的投影?呵呵,前面我们讲到的是以椭球体为参考来进行空间定位,一点都不直观,如果哪天你和妹纸约会,妹纸说她在(-2850017.472,4690744.523,3237959.973)或者(112°E,38°N),尼玛坑爹,这到底在哪个国家,离哥哥我有多远啊,不知道啊,不至于拿个尺子去测吧。这时候,泡妞高手们想出了一个办法,把球面投影到一个平面,用一个平面坐标(x,y)来表示地面点的位置,两点之间求距离是不是很容易啊?这时候你会发现那个妹子不就是隔壁那妞嘛,200米不到(囧!哈哈)。当然,投影最大的目的不是方便把妹纸,而是地图。所以投影就是把球面坐标转化为平面坐标,也就是3D到2D的转换。
投影有很多种,按性质分,比如等角投影,等积投影,等距投影,任意投影等。大家都知道,球面展开成平面,肯定是一个不严密(也可说不完美)的过程,会有不同程度的变形。如何选择呢?比如在航海上,就需要等角投影,如果方向错了就会差很多,我猜如果哥伦布那时知道这些就不会跑到美洲还以为到了印度吧。如果需要丈量面积,那就要选择等积投影了。
3、测量坐标有哪几种表示方式?
常见的测量坐标包括大地坐标(B、L、H)、空间直角坐标(X、Y、Z)、平面坐标(x、y、H)。具体参考相关教程。
4、坐标转换
终于讲到重点了,各种坐标怎样转换是大家最关心的。首先有一点要牢记:
同一参考椭球下,大地坐标与空间直角坐标之间的转换是严密的(数学关系对应),它们与平面坐标的转换是不严密的,需要做投影转换(想想也明白,把球面展成平面那可是难住了好多科学家呀)。而不同参考椭球之间的坐标转换永远都是非严密的。
坐标转换原理:
- 同一椭球下的转换
同一椭球下,大地坐标(B、L、H)与空间直角坐标(X、Y、Z)之间的转换是严密的,其公式为:
而大地坐标(B、L、H)与空间直角坐标(X、Y、Z)向平面直角坐标的转换属于非严密的,需要进行球面到平面的投影选择,通常将空间直角坐标转换为大地坐标,然后在大地坐标和平面直角坐标之间采用高斯正算和反算公式进行计算。
- 不同椭球下的转换
不同参考椭球下的坐标转换实质是基准的转换。如空间定位技术所采用的全球基准与地面网所采用的局部基准间的转换。通常的转换模型有布尔莎-沃尔夫模型和莫洛金斯基模型。这两种模型都常用且非常相似,布尔莎模型在进行全球或者较大范围内较为常用,但是莫洛金斯基模型可以克服布尔莎模型中旋转参数与平移参数相关性高的问题。
两个坐标系的转换通常有三维七参数模型和二维四参数模型。
布尔莎模型又称为七参数转换,或者七参数赫尔默特变换。该模型共采用7个参数,分别为三个平移参数(ΔX、ΔY、ΔZ)和三个旋转参数(ωx、 ωy、ωz)和一个尺度参数k。
上式是一个WGS84下的空间直角坐标转换到CGCS2000下的空间直角坐标的布尔莎模型,有七个未知参数,简单的求解,只需要3个公共点就可以了,如果要得到严密解,就需要更多的公共点进行最小二乘平差解算。而对于大地坐标,可以转成空间直角坐标再解算,也可以直接利用布尔莎模型。
5、遥感制图的投影和坐标系选择
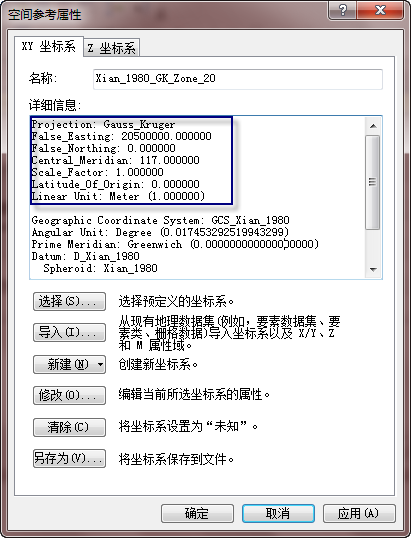
关于遥感影像的坐标系和投影,大家经常会听到所谓的地理坐标系(Geographic coordinate system)和投影坐标系(Projection coordinate system)的概念。打开Arcgis的坐标系文件夹也会发现这两个子文件夹。地理坐标系是以经纬度表示的,是一种球面坐标系,而投影坐标系是米或者千米等为单位的,是一种以xy表示的平面坐标系。下面是Arcgis中两种坐标系的定义:
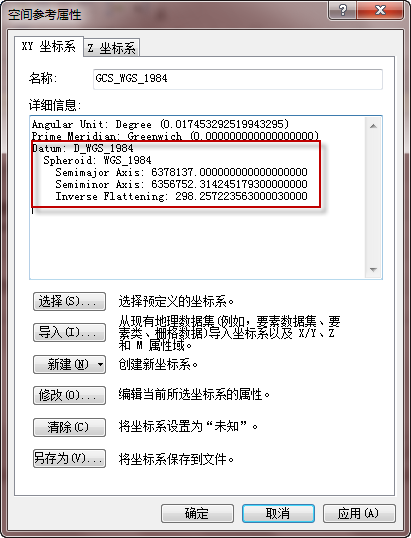
(a) 地理坐标系 (b)投影坐标系
上图中的左图a是WGS-84下的地理坐标系,我们可以看出它定义了一个WGS-84椭球体,然后是WGS84下的基准面。有了Spheroid和Datum就可以使用地理坐标系了。右图b是西安80坐标系下的投影坐标系,投影方式是高斯-克吕格投影。可以看出,它除了Gauss-Kruger投影参数外,还定义了Xian-1980地理坐标系。
有人会问,为什么投影坐标系要带一个地理坐标系呢?我们知道投影本质就是把球面投影到平面,那么投影就必须定义是用哪个球面坐标系来投影。比如UTM投影坐标系,我们熟知的是WGS84坐标系来投影,其实我们也可以用国家2000坐标系来投影,就我所知,在月球探索过程中,人们也用到了UTM投影,而这时用来投影的坐标系就是月球坐标系了。
我国常用地图投影的选择:
在我国,大中比例尺(≥1:50万)的地图一般选择高斯-克吕格投影,高斯-克吕格投影有3°和6°分带两种,1:2.5万-1:50万比例尺地形图采用经差6度分带,1:1万比例尺的地形图采用经差3度分带。小比例尺的地图(比如全中国地图)应采用等角正轴割圆锥投影,也就是兰勃特投影(Lambert Conformal Conic),但是小比例尺海图多选择等角正轴圆柱投影,也就是墨卡托投影。另外我们平时下载的遥感影像大都是WGS-84下的地理坐标系或者UTM投影坐标系。
下面就一个例子具体说下地理坐标系到投影坐标系的转换(投影的选择):
比如:北京的中心经纬度大致在(117°E,40°N),那么其在北京54投影坐标系下6°分带就应该选择Beijing 1954 GK Zone 20.prj或者Beijing 1954 GK Zone 20N.prj(后者会在横坐标前加上带号),中央经线=带号(比如20)*6-3。而在西安80投影坐标系下6°分带应该选择Xian 1980 GK Zone 20.prj。北京地区的遥感影像的UTM投影一般会选择WGS 1984 UTM Zone 50N,因为Zone为20*6-3的中央经线为117,左114,右120,正好覆盖北京,而东半球要加30(全球360/6共60个Zone)所以是50N,N表示北半球。此外,需要说明的是,跨带投影会造成较大的变形。很多人下载全球的植被图、夜间灯光图等,想要裁剪出自己需要的区域,原始数据往往是WGS84下的地理坐标系,而矢量数据多是UTM或者TM等投影坐标系,这时需要将矢量数据转换到地理坐标系再去裁剪,如果反过来将全球图去投影,会发现变形得很难看。
6、推荐一些好用的坐标转换工具
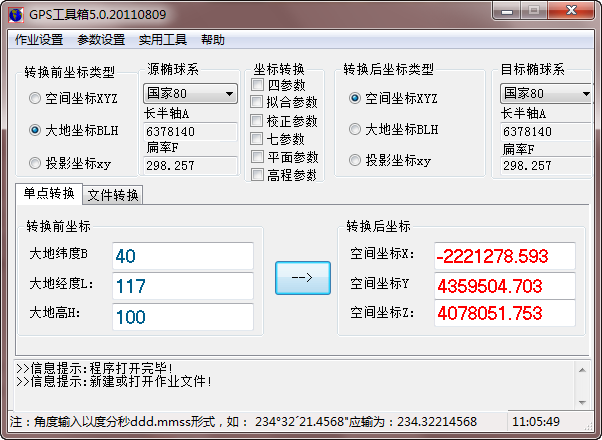
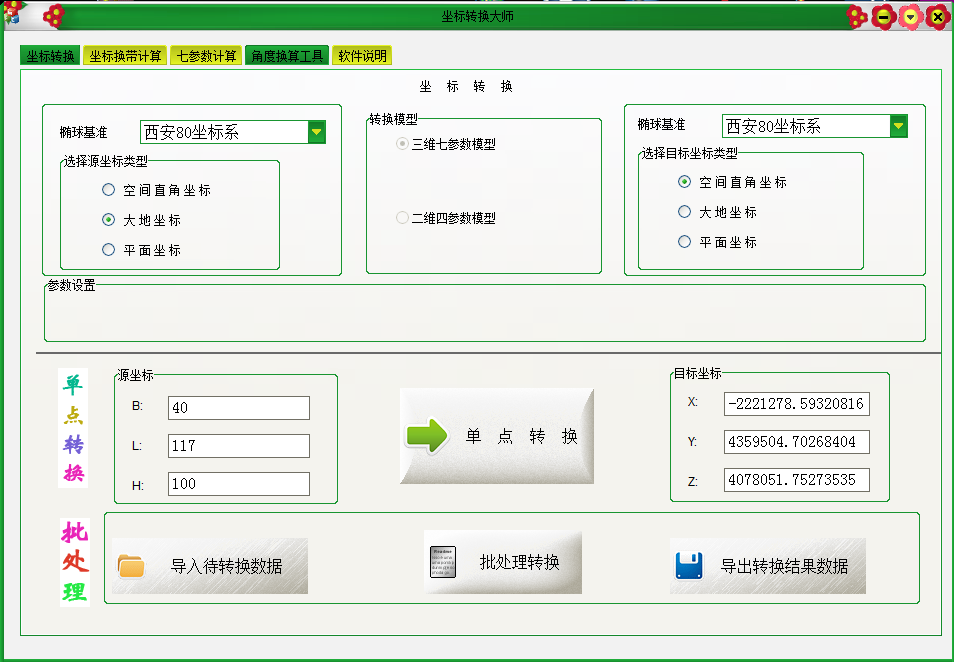
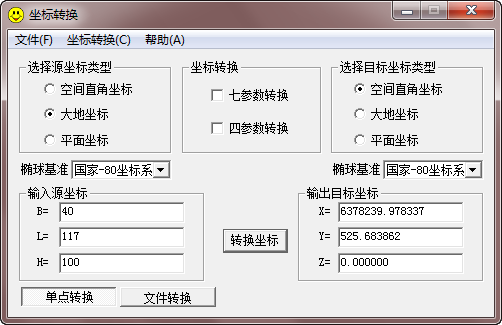
(1) 坐标转换工具:用过很多坐标转换工具,也自己写过,现在给大家推荐一款:GPS工具箱,发现它很容易用,精度也不错,这是下载地址:http://download.csdn.net/detail/rsyaoxin/5611283。可能大家平时会用的比较多的是Coord这个软件,但是我发现它结果老是不对,下面是几个软件的比较,第一个是GPS工具箱,第二个是我自己写的一个小软件,第三个是Coord,结果明显不对,不知道是不是我下载的Coord有问题。至于我自己写的这个工具,待有时间完善后我也会分享给大家用。
(2)开源坐标和投影转换库:Proj4。它的功能主要有经纬度坐标与地理坐标的转换,坐标系的转换,包括基准变换等。这是官方网站:http://trac.osgeo.org/proj/,可以下载到源码和文档,源码是C++所写,需要编译才能集成到你的程序使用。下面是我编译好的一个版本:http://download.csdn.net/detail/rsyaoxin/5611299
后记:好了,唠唠叨叨说了很多,如有不对之处,还请指出,可以直接留言,也可以到QQ群94935830来交流。








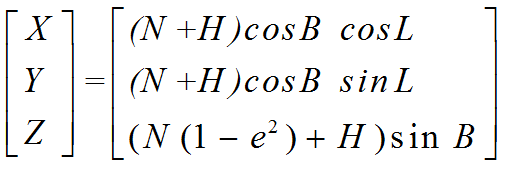
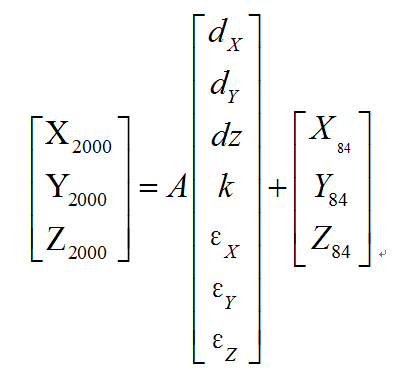
















 5954
5954

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








