【学习笔记整理】动态规划:背包问题之八大情况
【二次更新~】
前言:刚学习完《背包九讲》,理解的实际上有八讲。趁热打铁,整理一下这八大情况。里面还有我自己学习过程中遇到的问题解答。如果初学者想系统学习一下背包问题,可以看看喔。1.5W字,还请各位多多指教。
如果不想看我这篇小白垃圾文的话Q口Q,那就别浪费时间了(’’),可以看看ICPC裁判长写的哦~
初级背包问题详解 — 知乎专栏(01背包+完全背包+多重背包+二维费用背包+分组背包)
一、01背包问题
【题目背景描述】
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
【分析】
对于每一个物品而言,都有两种情况——选或者不选。想要得到最大价值我们通过枚举的方式来确定最大价值。(PS:从第3步敲黑板!!)
怎么枚举呢?我们可以这样:选择前 i 个物品时,体积0,1,……,V时,我们可以通过是否选择第 i 个物品来确定背包可以承装的最大价值。下面我们就举例子逐步分析,字数高能预警! 因为这是理解所有背包问题的基础关键!!!! 有了下面的分析后,往后背包问题的有关分析我们将不再赘述。
举个例子来说假设我现在有5件物品,背包体积是9;这5件物品的体积和价值分别是{1,2},{3,3},{2,5},{4,2},{3,6}
当选择前1个物品时,物品的是1,那么就有一下情况,如图所示(红字是最大价值。注意是当前的“最大价值”哦)

当只能选择1个物品时,在体积允许的情况下最大价值就可以知道了。
如果考虑到第 2 个物品(注意:是可以考虑到第2个物品了,但并不一定要选择第2个物品。是综合前2个物品来确定最大价值的)。如图所示

当总体积是0时,谁也装不下,最大价值是0;
当总体积是1时,无法选择物品2(即不选择物品2),只能装下物品1,总价值是2;(此时价值=考虑前1个物品的价值)
当总体积是2时,无法选择物品2(即不选择物品2),只能装下物品1(剩余1空间,物品2的体积是3,此时背包装不下),总价值是2;(此时价值=考虑前1个物品的价值)
当总体积是3时,允许装物品2。如果选择装物品2,剩余空间0,剩余空间的价值=0,总价值是3;如果不选择物品2,此时的价值=前1个物品时的最大价值=2。综上看来,选择装物品2时价值最大。所以总体积是3时,最大价值是3.
当体积≥4时,允许同时装下物品1和物品2,最大价值都是5,同时也都选择了物品2。(注意:还不能考虑第3个物品哦)
由此可见,选择第2个物品时价值最大。
-----------------最重要的一步来啦-------------------
以此类推,当选择前3个物品时,如图所示

当V=1,只能选择物品1,最大价值=2;
当V=2,可以选择物品1或物品3。选择物品3时,剩余空间价值=0,总价值=5;
当V=3,可以选择物品1、物品2或物品3。如果选择第3个物品,剩余1空间。没有物品3的剩余1空间的最大价值=2(因为已经选择第3个物品了,自然在剩下的1空间中就没有第3个物品了),总价值=5+2=7;如果不选择第3个物品,那么此时的最大价值=选择同体积下第2个物品的最大价值=3;综合,v=3时,最大价值=7。 【这地方一定要理解!很关键!】
以此类推,V=4时,最大价值=7;
当V=5时,如果选择第3个物品,剩余空间3,那么剩余空间3的最大价值=3。最大价值=5+3=8;如果不选择,那么此时的最大价值=选择同体积下第2个物品的最大价值=5。综合,V=5时,最大价值=8。
当V=6时,最大价值是三个物品都选。因为无论选择哪个物品,都有足够的剩余空间去装其他的物品。那么,最大价值=10。
由此可见,选择第3个物品时价值最大。
以此类推,选择前4个物品的情况如图所示

选择前5个物品的情况如图所示

到这里就稍稍总结一下。确定当前最大价值的思路是:是否选择第 i 个物品,如果选择,最大价值 = 第 i 个物品的价值 + 前 i-1 个物品的最大价值;
如果不选,最大价值 = 前 i-1 个物品的最大价值。比较两种情况,选出价值最大的情况即为当前的最大价值。
提醒:即使是剩余空间的价值,也一定是当V=剩余空间时的最大价值,因为对于每一步我们得到的都是当前的最大价值,所以式中的两种状态都代表当时的最大价值。
这样的话每行最后一列都代表选择前 i 个物品的最大价值。注意,因为数据的偶然性,最后一列呈现递增的趋势。在实际问题中,数据不一定是递增的,更多时候是无序的。
【代码展示】----------------- 二维常规解法 (AC代码)
#include <iostream>
#include <algorithm>
#define N 1010
using namespace std;
int n,m;
int f[N][N];
int main()
{
int v,w;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&v,&w);
for(int j=0;j<=m;j++){
f[i][j]=f[i-1][j]; //不选择第 i 个物品
if(j>=v)
f[i][j]=max(f[i][j],f[i-1][j-v]+w); //不选和选两种情况的最大值
}
}
int res=0;
for(int i=1;i<=n;i++)
res=max(res,f[i][m]);
printf("%d\n",res);
return 0;
}
【代码展示】------------------- 一维优化 (AC代码)
从二维解法不难看出,二维数组把“过去”的每一个值都记录了下来。这样的话,数据越大,所需要的空间就越多。因此,优化为一维数组更为简洁。
那么优化的原理是什么呢?就是不断更新当前的值。拿个比喻来说吧。我们有一个横线本子,每一行你都可以写一组数据。二维解法相当于一行记一组数据;一维解法相当于你只能用一行,想要记录某个数据就必须把相应位置上的原数据用橡皮擦掉,然后再写上新的数据,这就是更新。如果不需要更新,那就不用擦。(相应位置 = 当前总体积)
是关键点且必须注意的是,遍历体积时我们是从大到小遍历。为什么呢?那我们利用循环意义展开阐述。
- 外层for还是用来遍历原来二维数组的每一行(虽然现在已经没有二维数组了,但是表示的还是这个意义,只不过是用一维数组一直通过外层循环将每一行的值更新 ≈ 每一次的橡皮擦更新)
- 内层循环就是在更新二维数组(同上一个括号内的说法)的每一行中的每一列的值 ≈ 拿笔去修改数据。
- 因此我们还想用上一行的值得时候,就不能从前往后了,要从后往前,更新某行最后一个值的时候,其实前面的值存储的还是上一行的所有值,所以不受影响。 就是我们一定要保证之前的数据不能丢。从后往前是为了保存 意义 为前 i-1 物品的最大价值。
这个地方是比较绕的,当时我也弄了好半天才理解的。最好的理解就是,你自己举一些例子,然后用一维数组走一遍代码,边走边想数据是怎么更替的,可以拿纸拿笔画画写写。我就是这样过来的,真的很好用,光听别人说没用,别舍不得动笔。过程一定要慢,要清楚的知道每一步,一旦不清楚了就赶紧重新开始。三两遍下来你就懂了。
#include <iostream>
#include <algorithm>
#define N 1010
using namespace std;
int n,m;
int f[N];
int main()
{
int v,w;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&v,&w);
for(int j=m;j>=v;j++) //注意:必须从大到小遍历体积
f[j]=max(f[j],f[j-v]+w);
}
printf("%d\n",f[m]);
return 0;
}
【可能问题解答】(后文出现的所有笔记图片,皆是由本人的OneNote笔记转印过来,非转载或盗窃昂~)



注意:01背包是背包问题的基础哦,说什么也要把01背包理解好。如果不能理解,那就别往下看了,看了你也不懂。
二、完全背包问题
【题目背景】
把“每个物品只能用一次”改为“每个物品可以用无限次”。
【分析】
先看01背包,我们无论用二维数组还是用一维数组,都要保存前 i-1 物品的状态。为什么呢?因为我们每件物品只能选择一次。正因为如此,当选择第 i 个物品时,剩余空间的最大价值也要从前 i-1 个物品找,因为我们已经选过了、不能再选第i个物品了嘛。
那如果每件物品想选几次就选几次呢。那不就是说我选完了第i个物品之后,我还可以再选第i个物品嘛。
我知道你们不想动手,刚才让你们自己走一遍现在是不是疲惫了?哈哈,我来帮你们走一遍。但并不是全过程哦,只是其中具体的一步。又因为二维比较好理解,所以拿一维举例。
(可以先看下面的代码,再回来看分析)
比如背包总体积是7,然后现在到了体积为3的物品,走一遍就有
f【3】=max(f【3】,f【0】+w),
f【4】=max(f【4】,f【1】+w),
f【5】=max(f【5】,f【2】+w),
f【6】=max(f【6】,f【3】+w),
f【7】=max(f【7】,f【4】+w),
从中不难看出,f【6】时就用了更新过的f【3】,f【7】就用了更新过的f【4】。假设在max(,)中都是后者较大(取后者),那么f【6】中包含了1个f【3】,f【7】中包含了2个f【3】,这就实现了一个物品的多用。并且我们在这里的假设都是取max(,)的后者,假设条件简单。真实情况是取前取后都有可能,所以有更多的物品个数搭配。
【代码展示】--------------------- 二维常规解法 (AC代码)
是否使用二维解法,要看数据的范围。数据小,可以用;反之,会超时。在V=1010的数据下,会超时。
#include <iostream>
#include <algorithm>
#define N 1010
using namespace std;
int n,m;
int f[N][N];
int main()
{
int v,w;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&v,&w);
for(int j=0;j<=m;j++)
for(int k=0;k*v<=j;k++)
f[i][j]=max(f[i][j],f[i-1][j-k*v]+k*w); //这里对比01背包的二维解法哦
}
printf("%d\n",f[n][m]);
return 0;
}
【可能问题解答】


【代码展示】----------------------- 一维优化(AC代码)
这个代码就不会超时啦。
我们先来一个一维数组的 理解 版本(只贴出关键代码)
for(int i=1;i<=n;i++)
{
scanf("%d%d",&v,&w);
for(int j=m;j>=v;j--) //从大到小哦
for(int k=0;k*v<=j;k++) //控制个数
f[j]=max(f[j],f[j-k*v]+k*w);
}
printf("%d\n",f[m]);
标准代码
#include <iostream>
#include <algorithm>
#define N 1010
using namespace std;
int n,m;
int f[N];
int main()
{
int v,w;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&v,&w);
for(int j=v;j<=m;j++) //注意:这个体积是从小到大哦
f[j]=max(f[j],f[j-v]+w); //没有控制个数的k了哦
}
printf("%d\n",f[m]);
return 0;
}
三、多重背包问题
【题目背景】
和01背包差不多,把“每个物品只能选一次”改为“每个物品可以选择s次”。
【分析】
既然每个物体可以选择S次,那我们可以把这S次拆开。现在提供两种拆法。无论怎样拆分,最后的思路都是转换为01背包问题。
①拆成一个一个的。比如 5=1+1+1+1+1。
②通过二进制转十进制的原理进行拆分。比如 5 = 1 + 4。
1 2 4 可以表示0~7的任意数字;1 2 4 8 可以表示0~15的任意数字 ……
那么问题来了,如果次数恰好卡到10呢?如果用 1 2 4 8 可是会出现 11 的,这是不合适的。所以我们可以通过 10 - 1 - 2 - 4 = 3 得到我们想要的第4个数。此时就变成了 1 2 4 3 ,就可以得到 0 ~ 10 之间任意的一个数了。
【代码展示】---------------------------- 拆法①(AC代码)
#include <iostream>
#include <algorithm>
#define N 110 //注意这里是小数据哦
using namespace std;
int n,m;
int f[N];
int main()
{
int v,w,s;
scanf("%d%d",&n,&w);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&v,&w,&s);
for(int j=m;j>=v;j--) //回归01背包,从大到小。不懂看【分析】
for(int k=1;k<=s&&k*v<=j;k++) //注意k的含义
f[j]=max(f[j],f[j-k*v]+k*w);
}
printf("%d\n",f[m]);
return 0;
}
【代码展示】---------------------- 拆法②(AC代码)
二进制优化
#include <iostream>
#include <algorithm>
#include <vector>
#define N 2010 //数据更大了哦
using namespace std;
int n,m;
int f[N];
struct Good
{
int v,w;
};
int main()
{
int v,w,s;
vector<Good> goods;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&v,&w,&s);
for(int k=1;k<=s;k*=2) //按二进制打包、拆分
{
s-=k;
goods.push_back({k*v,k*w});
}
if(s>0) goods.push_back({s*v,s*w});
}
//将打包、拆好的都放入栈里。此时的栈就相当于01背包里面的数据。
//每一个数据都是01背包的物品性质
for(auto good:goods) //意思是:goods里面的内容通过新变量good依次遍历
for(int j=m;j>=good.v;j--)
f[j]=max(f[j],f[j-good.v]+good.w);
printf("%d\n",f[m]);
return 0;
}
也许看完代码你还是有疑惑,如果是 “ 明明是以二进制打包进入栈的,为什么还能表示出 0 ~ m 的任意数呢?”,那我就可以回答你啦。
想一下【可能问题解答1】里面的解释,是不是有点思路了?没错,虽然我们是打包进去的,但在数据更新过程中,会有多种多样的物品组合,自然可以表示出 0 ~ m 的任意数。
当然,上面所有的代码都可以用二维数组来写。我相信当你理解了一维优化后,二维解法对你来说并不困难。那下面的内容我就不用二维来做了哦。(敲字不易,望见谅Q^Q)
进一步优化。
如果数据规模达到了20000,还是有方法解决的。利用单调队列优化的方法就可以解决。但是 多重背包+单调队列优化 是《男人八题》里面的题目,难度系数大。而且我自己也不是很明白,不能误人子弟,所以就不说啦。
但如果有兴趣的话,可以看看下面的博客或视频哦。
dd大牛的《背包九讲》
《背包九讲》 11:10开始
四、混合背包问题
【题目背景】
有 N 种物品和一个容量是 V 的背包。
物品一共有三类:
第一类物品只能用1次(01背包);
第二类物品可以用无限次(完全背包);
第三类物品最多只能用 si 次(多重背包);
每种体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
si=−1 表示第 i 种物品只能用1次;
si=0 表示第 i 种物品可以用无限次;
si>0 表示第 i 种物品可以使用 si 次;
【分析】
由题目可以知道,混合背包问题就是01背包+完全背包+多重背包。由 “ 三、多重背包问题 ” 可以知道多重背包可以转换为01背包。所以混合背包问题的实质就是01背包+完全背包。解答的时候只要分别讨论就可以了。考虑到数据的规模,我们用二进制优化法来解决。
( 如果对01背包和完全背包解法有点模糊的伙伴,赶紧回看呀。)
【代码展示】 ( AC代码 )
#include <iostream>
#include <algorithm>
#include <vector>
#define N 1010
using namespace std;
int n,m;
int f[N];
struct Good
{
int v,w,s;
};
int main()
{
int v,w,s;
vector<Good> goods;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&v,&w,&s);
if(s<0) goods.push_back({v,w,-1});
else if(s==0) goods.push_back({v,w,0});
else
{
for(int k=1;k<=s;k*=2)
{
s-=k;
goods.push_back({k*v,k*w,-1});
}
if(s>0) goods.push_back({s*v,s*w,-1});
}
}
for(auto good:goods)
{
if(good.s==-1)
for(int j=m;j>=good.v;j--)
f[j]=max(f[j],f[j-good.v]+good.w);
else
for(int j=good.v;j<=m;j++)
f[j]=max(f[j],f[f-good.v]+good.w);
}
printf("%d\n",f[m]);
return 0;
}
五、二维费用的背包问题
【题目背景】
除了体积外,又加了质量。即不超过体积和质量的情况下,最大价值是多少。
【分析】
只有体积的时候,我们用的是一维数组,里面的 j 表示总体积是 j 时候的最大价值。再加质量的话,只要用二维数组就可以了。f [ i ] [ j ] 表示体积为 i ,质量为 j 时的最大价值。它的实质还是01背包。
【代码展示】( AC代码 )
#include <iostream>
#include <algorithm>
#define N 1010
using namespace std;
int n,V,M;
int f[N][N];
int main()
{
int v,m,w;
scanf("%d%d%d",&n,&V,&M);
for(int i=1;i<=n;i++)
{
scanf("%d%d%d",&v,&m,&w);
for(int j=V;j>=v;j--)
for(int k=M;k>=m;k--)
f[j][k]=max(f[j][k],f[j-v][k-m]+w);
}
printf("%d\n",f[V][M]);
return 0;
}
如果不想用一维优化下的二维解法,想用由原二维解法得来的解法的话,就要用三维数组了哦。第一维是物品,第二维是体积,第三维是质量。
六、分组背包问题
【题目背景】
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vij,价值是 wij,其中 i 是组号,j 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。输出最大价值。
输入格式
第一行有两个整数 N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有 N 组数据:
每组数据第一行有一个整数 Si,表示第 i 个物品组的物品数量;
每组数据接下来有 Si 行,每行有两个整数 vij,wij,用空格隔开,分别表示第 i 个物品组的第 j 个物品的体积和价值;
【分析】
每组里的物品互斥,即在每一组物品中,仅能选择一件物品或者不选。那么可能的选法就有s+1种(可能不选,可能选第一个,也可能选第二个,……,也可能选第s个)。这样我们就可以知道选择组内的哪个物品使得前 i-1 组的价值最大。
【代码展示】( AC代码 )
#include <iostream>
#include <algorithm>
#define N 1010
using namespace std;
int n,m;
int f[N];
int main()
{
int s,v[N],w[N];
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&s);
for(int j=1;j<=s;j++) scanf("%d%d",&v[j],&w[j]);
for(int k=m;k>=0;k--) //体积从大到小
for(int j=1;j<=s;j++) //遍历当前组
if(k>=v[j])
f[k]=max(f[k],f[k-v[j]]+w[j]); //实际上是求选择组内的哪一个物品使得前i组的价值最大
}
printf("%d\n",f[m]);
return 0;
}
下面是样例 f 数组的变化情况。(非数组数字仅为输入)

值得一提的是,分组背包是多重背包的拓展,多重背包是分组背包的特例。多重背包是每个物品有S件,如果分组背包的数据是:每组都是相同的物品,那么虽然是“每组”,实际上=“每个”物品有S件。
所以分组背包问题是一个更大的问题。因此,虽然多重背包有二进制优化和单调队列优化,但对于分组背包并不适合。
七、背包问题求方案数
【题目背景】
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出 最优选法的方案数。注意答案可能很大,请输出答案模 109+7 的结果。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示 方案数 模 109+7 的结果。
【分析】
题目要求的是“最优选法”,那我们肯定需要知道最大价值,f [ j ] 必须有;那么方案数怎么办呢?我们可以再开一个表示方案数的数组 g [ i ] ,表示当体积恰好为 i 时的方案数。
注意一个关键字 “ 恰好 ” 。看前面的六大问题,f [ j ] 刚开始都是0,在后续的计算中表示体积不超过 j 的最大价值。如果 f [ 0 ] = 0 , f [ 1 … m ] = - ∞ ,那么在后续计算中表示体积恰好是 j 的最大价值。
因为我们要求方案数,所以肯定选择“恰好”;如果选择“不超过”,方案数会重复计算。
【代码展示】( AC代码 )
#include <iostream>
#include <algorithm>
#define N 1010
#define mod 1000000007
#define INF 1000000
using namespace std;
int n,m;
int f[N],g[N];
int main()
{
int v,w;
for(int i=1;i<=m;i++) f[i]=-INF;
g[0]=1; //当体积为0时,只有一种方案:什么也不装
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&v,&w);
for(int j=m;j>=v;j--)
{
int t=max(f[j],f[j-v]+w); //当前的最大价值————三种情况
int s=0; //1、等于前面的
if(t==f[j]) s+=g[j]; //2、等于后面的
if(t==f[j-v]+w) s+=g[j-v]; //3、前面=后面
s%=mod; //s表示当前的方案数(若是两种情况自然要两种情况都加)
f[j]=t;
g[j]=s;
}
}
int maxx=0;
for(int i=0;i<=m;i++) maxx=max(maxx,f[i]);
int res=0;
for(int i=0;i<=m;i++)
if(f[i]==maxx){
res+=g[i];
res%=mod;
}
printf("%d\n",res);
return 0;
}
【可能问题解答】—— 有关初始化不同的问题



可以手动模拟一下 f [ j ] 数组的变化过程。(自己太懒Q^Q,一位学姐的图)

八、背包问题求具体方案
【题目背景】
在满足最大价值的前提下,输出字典序最小的所选物品编号。
【分析】




【代码展示】(AC代码)
#include <iostream>
#include <algorithm>
#define N 1010;
using namespace std;
int n,m;
int f[N][N],v[N],w[N];
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);
for(int i=n;i>=1;i--) //01背包是从前往后开始选,这个是从后往前开始选
for(int j=0;j<=m;j++){ //因为二维可以记录到每一个状态,所以体积无论是从大到小还是从小到大都是一样的哦
//之前之所以从大到小,是因为我们要保留前一个状态(忘了的,赶紧回看哦)
f[i][j]=f[i+1][j]; //代表的是逻辑上的上一个状态,千万不要由于是从后往前遍历的缘故而晕了哦
if(j>=v[i]) f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
}
int vol=m;
for(int i=1;i<=n;i++)
if(vol>=v[i]&&f[i][vol]==f[i+1][vol-v[i]]+w[i]){
printf("%d ",i);
vol-=v[i];
}
return 0;
}
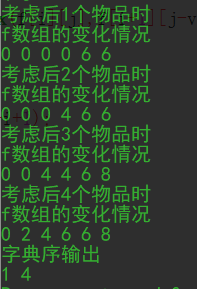
注意,必须一直考虑到第一个物品时,f [ j ] 数组储存的才是体积为0~V时的最终最大价值。下面是样例输出的 f 数组变化情况。(注意是选择“后”几个物品哦)
后言
参考博客:
yam bean
除了上面的八大背包,还有 有依赖的背包问题,这个涉及到树的知识,但是目前我还没有搞懂,所以有兴趣的伙伴就看上文帖的链接哦。
笔记结束。(但未来仍会更新或出新笔记)






















 650
650











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








