Oh My Holy FFF
Time Limit: 5000/2500 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)Total Submission(s): 1074 Accepted Submission(s): 299
Problem Description
N soldiers from the famous "*FFF* army" is standing in a line, from left to right.
You, as the captain of *FFF*, want to divide them into smaller groups, but each group should still be continous in the original line. Like this:
In your opinion, the number of soldiers in each group should be no more than L.
Meanwhile, you want your division be "holy". Since the soldier may have different heights, you decide that for each group except the first one, its last soldier(which is the rightmost one) should be strictly taller than the previous group's last soldier. That is, if we set bi as the height of the last soldier in group i. Then for i >= 2, there should be b i > b i-1.
You give your division a score, which is calculated as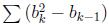 , b
0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.
, b
0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.
Given the heights of all soldiers, please tell us the best score you can get, or declare the division as impossible.
o o o o o o o o o o o o o o o o o o /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ /F\ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \ / \
You, as the captain of *FFF*, want to divide them into smaller groups, but each group should still be continous in the original line. Like this:
o o o | o o o o | o o o o o o | o o o o o /F\ /F\ /F\ | /F\ /F\ /F\ /F\ | /F\ /F\ /F\ /F\ /F\ /F\ | /F\ /F\ /F\ /F\ /F\ / \ / \ / \ | / \ / \ / \ / \ | / \ / \ / \ / \ / \ / \ | / \ / \ / \ / \ / \
In your opinion, the number of soldiers in each group should be no more than L.
Meanwhile, you want your division be "holy". Since the soldier may have different heights, you decide that for each group except the first one, its last soldier(which is the rightmost one) should be strictly taller than the previous group's last soldier. That is, if we set bi as the height of the last soldier in group i. Then for i >= 2, there should be b i > b i-1.
You give your division a score, which is calculated as
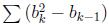 , b
0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.
, b
0 = 0 and 1 <= k <= M, if there are M groups in total. Note that M can equal to 1.
Given the heights of all soldiers, please tell us the best score you can get, or declare the division as impossible.
Input
The first line has a number T (T <= 10) , indicating the number of test cases.
For each test case, first line has two numbers N and L (1 <= L <= N <= 10 5), as described above.
Then comes a single line with N numbers, from H1 to Hn, they are the height of each soldier in the line, from left to right. (1 <= H i <= 10 5)
For each test case, first line has two numbers N and L (1 <= L <= N <= 10 5), as described above.
Then comes a single line with N numbers, from H1 to Hn, they are the height of each soldier in the line, from left to right. (1 <= H i <= 10 5)
Output
For test case X, output "Case #X: " first, then output the best score.
Sample Input
2 5 2 1 4 3 2 5 5 2 5 4 3 2 1
Sample Output
Case #1: 31 Case #2: No solution
来自论文的分析:


思路:
朴素的DP 是 DP[i] = max(DP[j] - b[j]) + b[i]*b[i] ( i-l <= j <= i-1 ) 但是这样会超时(O(n^2)) 可以发现每次求DP[i] 的时候 实际就是求 区间[i-l,i-1] DP[j]-b[j]的最大值,因此可以利用线段树优化,此时还需要解决一个问题:就是如何保证每次求DP[i]的时候保证区间[i-l,i-1] 的每个人的身高都是比自己矮的? 可以进行先排序,让矮的人先选,如果身高一样就让序号在后的先选,这样就不会有冲突了(单点更新的时候)。 每次查询的时候单点更新即可。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
const int maxn = 1e5+10;
int n, l;
ll dp[maxn];
struct Num
{
ll h;
int idx;
Num(ll _h = 0, int _idx = 0):h(_h), idx(_idx){}
bool operator < (const Num &other) const
{
if(h != other.h)
return h < other.h;
else
return idx > other.idx;
}
};
vector<Num> v;
struct SegMent
{
int lson, rson;
ll maxx;
int mid()
{
return (lson+rson) >> 1;
}
}tree[maxn*4];
void pushup(int rt)
{
tree[rt].maxx = max(tree[rt<<1].maxx, tree[rt<<1|1].maxx);
}
void build(int L, int R, int rt)
{
tree[rt].lson = L;
tree[rt].rson = R;
tree[rt].maxx = -1;
if(L == R)
return ;
int mid = tree[rt].mid();
build(L, mid, rt<<1);
build(mid+1, R, rt<<1|1);
}
void update(int pos, int l, int r, int rt, ll x)
{
if(l == r)
{
tree[rt].maxx = x;
return;
}
int mid = tree[rt].mid();
if(pos <= mid)
update(pos, l, mid, rt<<1, x);
else
update(pos, mid+1, r, rt<<1|1, x);
pushup(rt);
}
ll query(int L, int R, int l, int r, int rt)
{
if(l >= L && r <= R)
{
return tree[rt].maxx;
}
int mid = tree[rt].mid();
ll ret;
if(R <= mid)
ret = query(L, R, l, mid, rt<<1);
else if(L > mid)
ret = query(L, R, mid+1, r, rt<<1|1);
else
ret = max(query(L, R, l, mid, rt<<1), query(L, R, mid+1, r, rt<<1|1));
return ret;
}
void solve()
{
update(0, 0, n, 1, 0);
for(int i = 0; i < v.size(); i++)
{
int ni = v[i].idx;
ll nh = v[i].h;
ll tm = query(max(ni-l, 0), ni-1, 0, n, 1);
if(tm >= 0)
{
dp[ni] = tm + nh*nh;
update(ni, 0, n, 1, dp[ni]-nh);
}
if(ni == n)
break;
}
if(dp[n] <= 0)
printf("No solution\n");
else
printf("%I64d\n",dp[n]);
}
int main()
{
int T;
scanf("%d", &T);
for(int kase = 1; kase <= T; kase++)
{
v.clear();
memset(dp, -1, sizeof(dp));
scanf("%d%d", &n, &l);
for(int i = 1; i <= n; i++)
{
ll h;
scanf("%I64d", &h);
v.push_back(Num(h, i));
}
sort(v.begin(), v.end());
build(0, n, 1);
printf("Case #%d: ", kase);
solve();
}
return 0;
}






















 691
691

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








