HDU 4565 So Easy!（矩阵快速幂+数学）

题目链接：
HDU 4565 So Easy!
题意：

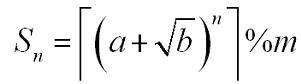
$┌x┐$是向上取整的意思，如$┌3.14┐=4$。给出$a，b和n，m$计算$Sn$.
分析：

首先需要想到(a+sqrt(b))^n的结果能写成A+B*sqrt(b)的形式。
n=1时是a+1*sqrt(b) ;                            A=a,               B=1;
n=2时是(a^2+b)+2*a*sqrt(b) ;                    A=a^2+b,           B=2*a;
n=3时是(a^3+3*a*b)+(3*a^2+b)*sqrt(b);           A=a^3+3*a*b,       B=3*a^2+b;
n=4时是(a^4+6*a^2*b+b^2)+(4*a^3+4*a*b)*sqrt(b); A=a^4+6*a^2*b+b^2, B=4*a^3+4*a*b
....
不难得到矩阵转换式:
| a  b |* | A(i-1) | = | A(i) |
| 1  a |  | B(i-1) |   | B(i) |
接下来就是矩阵快速幂计算n时的A和B了。虽然我知道最终结果是
long long res=(tmp.data[1][1]+(long long)(ceil((tmp.data[2][1]*1.0*sqrt(b*1.0)))))%mod;
其中tmp.data[1][1]=A,tmp.data[2][1]=B,这样是不讲道理，也不合理的，因为直接对B取模再乘以一个根号数，肯定对结果有影响
虽然样例也能过，但是我已经想不到别的办法了，交了一发，果然WA了，又发现题目中有个条件
(a-1)^2<b<a^2,仔细想了一下，还是找不到优化的方法，无奈搜题解，不服不行啊。
若(a+sqrt(b))^n=A+B*sqrt(b)，则(a-sqrt(b))^n=A-B*sqrt(b)
又因为(a-1)^2<b<a^2，所以a-1<b<a，所以0<a-sqrt(b)<1,所以0<(a-sqrt(b))^n<1
所以0<A-B*sqrt(b)<1,所以A-1<B*sqrt(b)<A,又因为是向上取整的，所以ceil(A+B*sqrt(b))=2*A,真是太强了！

//124MS 1400K
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;

long long a,b,n,mod;

struct Matrix{
    int row,col;
    long long data[10][10];
};

inline Matrix mul(Matrix a,Matrix b)
{
    Matrix ans;
    ans.row=a.row,ans.col=b.col;
    memset(ans.data,0,sizeof(ans.data));
    for(int i=1;i<=ans.row;i++){
        for(int j=1;j<=ans.col;j++){
            for(int k=1;k<=a.col;k++){
                ans.data[i][j]+=a.data[i][k]*b.data[k][j]%mod;
                ans.data[i][j]%=mod;
            }
        }
    }
    return ans;
}

inline Matrix quick_power(Matrix a,long long n)
{
    Matrix ans,tmp=a;
    ans.row=ans.col=a.row;
    memset(ans.data,0,sizeof(ans.data));
    for(int i=1;i<=ans.row;i++) ans.data[i][i]=1;
    while(n){
        if(n&1) ans=mul(ans,tmp);
        tmp=mul(tmp,tmp);
        n>>=1;
    }
    return ans;
}

int main()
{
    freopen("Min.txt","r",stdin);
    while(~scanf("%lld%lld%lld%lld",&a,&b,&n,&mod)){
        a%=mod,b%=mod;
        Matrix ans,tmp;
        ans.row=ans.col=2;
        ans.data[1][1]=a,ans.data[1][2]=b;
        ans.data[2][1]=1,ans.data[2][2]=a;
        ans=quick_power(ans,n-1);
        tmp.row=2,tmp.col=1;
        tmp.data[1][1]=a,tmp.data[2][1]=1;
        tmp=mul(ans,tmp);
        //long long res=(tmp.data[1][1]+(long long)(ceil((tmp.data[2][1]*1.0*sqrt(b*1.0)))))%mod;
        long long res=tmp.data[1][1]*2%mod;
        printf("%lld\n",res);
    }
    return 0;
}