什么是向量?
合理定义加法和数乘、符合公设的“东西”就是向量;
向量空间对加法及数乘这两种基本运算保持封闭。
如果给向量空间添加点积(长度和角度、欧式距离和余弦距离)的定义,就构成了欧几里得空间。
例如说,
-
颜色可以是“向量”,三原色是“基底”

-
多项式函数是“向量”, x 2 + 5 = [ 5 0 1 0 ⋯ ] x^2+5=\begin{bmatrix} 5\\ 0\\ 1\\ 0\\ \cdots \end{bmatrix} x2+5= 5010⋯
-
信号是“向量”,可以合成和分解;
向量 v ⃗ = [ 1 2 ] ∈ R 2 \vec{v} = \begin{bmatrix} 1\\ 2 \end{bmatrix} \in \mathcal{R}^2 v=[12]∈R2是二维坐标系标准正交基底向量的缩放和(线性组合): 1 i ^ + 2 j ^ 1\hat{i} + 2 \hat{j} 1i^+2j^的简记;如果基底变换用矩阵的形式表示, I = [ 1 0 0 1 ] I=\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} I=[1001], x = [ 1 2 ] x=\begin{bmatrix} 1\\ 2 \end{bmatrix} x=[12],这里 I I I是“恒等变换”: I x = x Ix=x Ix=x。
什么是线性系统(多元一次联立方程组、矩阵)?
系统,也被称作映射、函数、变换、算子,输入一个“东西”,输出一个“东西”,是一个“集合”到另一个“集合”的映射关系;
其中,满足叠加性( f ( x ⃗ + y ⃗ ) = f ( x ⃗ ) + f ( y ⃗ ) f(\vec {x} + \vec {y}) = f(\vec{x}) + f(\vec{y}) f(x+y)=f(x)+f(y))和比例性( f ( k x ⃗ ) = k f ( x ⃗ ) f(k\vec {x}) = kf(\vec{x}) f(kx)=kf(x))的是“线性系统”。
- 线性方程组是“线性系统”,以矩阵的形式简记系数时,我们更关注列向量的缩放和(线性组合),而不是将每行视作一个直线(超平面)约束,关注它们的交点;
- 向量 x x x是“输入”,矩阵 A A A是“线性系统”,向量 b b b是“输出”,如果从函数的语言说,解线性方程组就是求逆映射/反函数,可以从“值域”、“到达域”、“单射”,“满射”,理解方程组的“有解”、“唯一解”、“均有解”;;
- 转置是“线性系统”,前缀和、差分是“线性系统”,微分、积分也是“线性系统”,旋转、投影是“线性系统”:符合叠加性和比例性。
在二维视角下说,考虑线性系统操纵的是基底(空间),要满足输入直线,输出直线,输入零,输出零,网格线保持平行且“均匀”等距分布(旋转、投影也是线性变换,可以写作矩阵乘法的形式)。
矩阵运算和相关概念
-
矩阵乘法:多个变换相继作用,例如 M 2 ( M 1 x ) = ( M 2 M 1 ) x M_2(M_1 x) = (M_2 M_1) x M2(M1x)=(M2M1)x,矩阵乘法最初是用于表示线性方程组的解法(左乘是行视角行变换,右乘是列视角列变换);
-
行列式:系统对空间的挤压(拉伸)作用的度量,表现为方向(正、负)和大小(面积、体积之比);如果行列式为零,说明该变换对空间进行了塌陷变换,减小了维度,该变换是不可逆的,变换后的维度被称为“秩”,对应着矩阵“列向量”张成空间的维度(去除摆烂向量得到最大无关组,构成了该张成空间的一组基);
-
对于某些特定的向量而言,应用线性变换 A A A,并没有离开它自身(缩放)张成的直线, A A A相当于一个“标量” λ \lambda λ(或者说 λ I \lambda I λI),这些向量就被称为“特征向量”,这个“标量”度量了缩放方向与大小,被称为“特征值”。尤其对于旋转变换而言,“特征向量”就是“旋转轴”。
例一:差分、前缀和、矩阵的逆
例如说,
A
x
=
[
1
0
0
−
1
1
0
0
−
1
1
]
[
x
1
x
2
x
3
]
=
[
x
1
x
2
−
x
1
x
3
−
x
2
]
=
b
Ax = \begin{bmatrix} 1 & 0 & 0\\ -1 & 1 & 0\\ 0 & -1 & 1\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix} = \begin{bmatrix} x_1\\ x_2 - x_1\\ x_3 - x_2\\ \end{bmatrix}=b
Ax=
1−1001−1001
x1x2x3
=
x1x2−x1x3−x2
=b
考虑
A
A
A列向量的线性组合,它起到的变换作用是一阶差分。
如果输入
x
=
[
1
4
9
]
x=\begin{bmatrix} 1 \\ 4 \\ 9 \end{bmatrix}
x=
149
,自然地,线性系统的输出是
b
=
[
1
3
5
]
b=\begin{bmatrix} 1 \\ 3 \\ 5 \end{bmatrix}
b=
135
。
这是已知系统、输入,求得输出,我们称之为前向“传播”。
那么如果考虑求解线性方程组,即在已知“线性系统”和“输出”的前提下,
求得“输入”呢?对于当前的差分系统来讲,逆运算是前缀和,因此并不困难从输出到输入。
如果输出是
b
=
[
b
1
b
2
b
3
]
b=\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}
b=
b1b2b3
,那么很自然的,输入应该是
x
=
[
b
1
b
1
+
b
2
b
1
+
b
2
+
b
3
]
x=\begin{bmatrix} b_1 \\ b_1+b_2 \\ b_1 + b_2 + b_3 \end{bmatrix}
x=
b1b1+b2b1+b2+b3
,
我们关注原点(零点),假如说输出的
b
=
0
⃗
b=\vec{0}
b=0,那么输入的
x
x
x是唯一的。
同时,我们还可以写出这一线性变换的逆变换
A
−
1
=
[
1
0
0
1
1
0
1
1
1
]
A^{-1} = \begin{bmatrix} 1 & 0 & 0\\ 1 & 1 & 0\\ 1 & 1 & 1\\ \end{bmatrix}
A−1=
111011001
,使得
A
−
1
b
=
x
A^{-1}b=x
A−1b=x。
如果是这样的呢?
C
x
=
[
1
0
−
1
−
1
1
0
0
−
1
1
]
[
x
1
x
2
x
3
]
=
[
x
1
−
x
3
x
2
−
x
1
x
3
−
x
2
]
=
[
b
1
b
2
b
3
]
Cx = \begin{bmatrix} 1 & 0 & -1\\ -1 & 1 & 0\\ 0 & -1 & 1\\ \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix} = \begin{bmatrix} x_1 - x_3\\ x_2 - x_1\\ x_3 - x_2\\ \end{bmatrix}=\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}
Cx=
1−1001−1−101
x1x2x3
=
x1−x3x2−x1x3−x2
=
b1b2b3
第一个发现是,我们将
[
x
1
−
x
3
x
2
−
x
1
x
3
−
x
2
]
\begin{bmatrix} x_1 - x_3\\ x_2 - x_1\\ x_3 - x_2\\ \end{bmatrix}
x1−x3x2−x1x3−x2
所有项相加为零,可是
[
b
1
b
2
b
3
]
\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}
b1b2b3
所有项相加却不恒为零。
这意味着,
C
C
C的列向量张成空间(所有线性组合构成的向量空间)不是一个“点”(零维),不是一条“直线”(一维),
而是一个“平面”(二维),
x
+
y
+
z
=
0
x+y+z=0
x+y+z=0。
第二个发现是,只要输入
x
=
c
[
1
1
1
]
x=c\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}
x=c
111
都满足输出的
b
=
0
⃗
b=\vec{0}
b=0。
这说明有许多本身并不在原点的点(向量)经历该线性变换后,空间发生了塌陷,被挤压至零点(验证一下,
det
(
C
)
=
0
\det(C) = 0
det(C)=0,意味着基底体积变为0)。因此,并不存在这样的
C
−
1
C^{-1}
C−1(
C
C
C是不可逆的),能够将有损压缩的文件恢复原状。反证法:我们假设存在,
C
x
=
b
Cx=b
Cx=b,现存在
x
≠
0
⃗
x\ne \vec{0}
x=0,
b
=
0
⃗
b=\vec{0}
b=0,那么:
C
−
1
C
x
=
C
−
1
b
C^{-1}Cx=C^{-1}b
C−1Cx=C−1b,与假设相互矛盾。
只有双射函数 A ( x ) A(x) A(x)(对应满秩矩阵),才有反函数 A − 1 ( x ) A^{-1}(x) A−1(x)
例二:旋转矩阵与倍半角公式
「旋转」满足叠加、数乘,因而是一个线性变换。
我们可以用矩阵的形式进行描述,倘若我们要将向量
x
x
x逆时针旋转
θ
\theta
θ角,如何写这个矩阵呢?从基变换的视角看,这意味着我们要将坐标系
i
^
,
j
^
\hat{i}, \hat{j}
i^,j^同样逆时针旋转
θ
\theta
θ角。
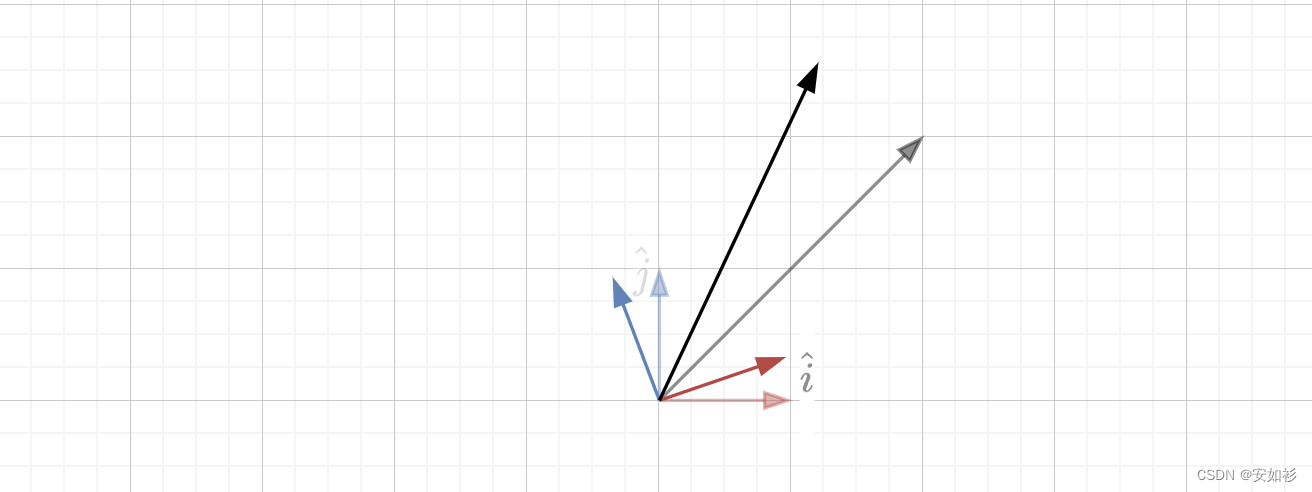
然后将新基底 i ^ ′ , j ^ ′ \hat{i}^\prime, \hat{j}^\prime i^′,j^′作为矩阵的列,就得到了旋转矩阵:
A = [ cos θ − sin θ sin θ cos θ ] A=\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin\theta & \cos\theta \end{bmatrix} A=[cosθsinθ−sinθcosθ]
我们能从旋转矩阵(系统、变换、函数、算子)获得什么有趣的发现呢?
考虑 A ( A x ) = ( A A ) x = A 2 x A(Ax) = (AA)x = A^2x A(Ax)=(AA)x=A2x, A 2 A^2 A2意味着旋转两次(旋转两倍),即:
[ cos θ − sin θ sin θ cos θ ] 2 = [ cos 2 θ − sin 2 θ sin 2 θ cos 2 θ ] \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin\theta & \cos\theta \end{bmatrix}^2 = \begin{bmatrix} \cos 2\theta & -\sin 2\theta \\ \sin 2\theta & \cos 2\theta \end{bmatrix} [cosθsinθ−sinθcosθ]2=[cos2θsin2θ−sin2θcos2θ]
不妨把矩阵进行平方,进行观察:
[ cos θ − sin θ sin θ cos θ ] [ cos θ − sin θ sin θ cos θ ] = [ cos 2 θ − sin 2 θ − 2 cos θ sin θ 2 cos θ sin θ cos 2 θ − sin 2 θ ] \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin\theta & \cos\theta \end{bmatrix} = \begin{bmatrix} \cos^2 \theta -\sin^2 \theta & -2 \cos \theta \sin \theta \\ 2 \cos \theta \sin \theta & \cos^2 \theta -\sin^2 \theta \end{bmatrix} [cosθsinθ−sinθcosθ][cosθsinθ−sinθcosθ]=[cos2θ−sin2θ2cosθsinθ−2cosθsinθcos2θ−sin2θ]
于是,我们用矩阵乘法推导出了倍角公式。真是太酷了!
例三:椭圆面积公式
我们将单位圆通过
x
=
(
cos
θ
sin
θ
)
x=\begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix}
x=(cosθsinθ)表示,对单位圆进行坐标变换
A
=
[
a
0
0
b
]
A=\begin{bmatrix} a & 0\\ 0 & b \end{bmatrix}
A=[a00b](分别将
x
,
y
x,y
x,y轴单位基底做
a
,
b
a,b
a,b拉伸),得到椭圆:
A
x
=
(
a
cos
θ
b
sin
θ
)
Ax = \begin{pmatrix} a\cos \theta \\ b\sin \theta \end{pmatrix}
Ax=(acosθbsinθ)
二阶行列式代表变换前后的有向面积之比,因此 S 椭圆 S 单位圆 = ∣ a 0 0 b ∣ \frac{S_{椭圆}}{S_{单位圆}} = \begin{vmatrix} a & 0\\ 0 & b \end{vmatrix} S单位圆S椭圆= a00b ,故:
S 椭圆 = π a b S_{椭圆} = \pi ab S椭圆=πab






















 2101
2101











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








