题目:
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 13445 | Accepted: 6447 |
Description
Some cows like each other and want to be within a certain distance of each other in line. Some really dislike each other and want to be separated by at least a certain distance. A list of ML (1 <= ML <= 10,000) constraints describes which cows like each other and the maximum distance by which they may be separated; a subsequent list of MD constraints (1 <= MD <= 10,000) tells which cows dislike each other and the minimum distance by which they must be separated.
Your job is to compute, if possible, the maximum possible distance between cow 1 and cow N that satisfies the distance constraints.
Input
Lines 2..ML+1: Each line contains three space-separated positive integers: A, B, and D, with 1 <= A < B <= N. Cows A and B must be at most D (1 <= D <= 1,000,000) apart.
Lines ML+2..ML+MD+1: Each line contains three space-separated positive integers: A, B, and D, with 1 <= A < B <= N. Cows A and B must be at least D (1 <= D <= 1,000,000) apart.
Output
Sample Input
4 2 1 1 3 10 2 4 20 2 3 3
Sample Output
27
题意:
n头牛编号1~n。按照编号顺序排成一排。有ML对关系好的牛的信息,(AL,BL,DL)。有MD对关系差的牛的信息,(AD,BD,DD)。要求牛AL与牛BL之间的最大距离为DL,牛AD与牛BD之间的最大距离为DD。在满足这些条件的方法中,求1号牛与n号牛的最大距离。不存在输出-1,无限大输出-2。
方法:差分约束(摘自点击打开链接)
一、何为差分约束系统:
差分约束系统(system of difference constraints),是求解关于一组变数的特殊不等式组之方法。如果一个系统由n个变量和m个约束条件组成,其中每个约束条件形如xj-xi<=bk(i,j∈[1,n],k∈[1,m]),则称其为差分约束系统(system of difference constraints)。亦即,差分约束系统是求解关于一组变量的特殊不等式组的方法。
通俗一点地说,差分约束系统就是一些不等式的组,而我们的目标是通过给定的约束不等式组求出最大值或者最小值或者差分约束系统是否有解。
比如:
二、差分约束系统的求解:
差分约束系统可以转化为图论来解决,对应于上面的不等式组,如果要求出x3-x0的最大值的话,叠加不等式可以推导出x3-x0<=7,最大值即为7,我们可以通过建立一个图,包含6个顶点,对每个xj-xi<=bk,建立一条i到j的有向边,权值为bk。通过求出这个图的x0到x3的最短路可以知道也为7,这是巧合吗?并不是。
之所以差分约束系统可以通过图论的最短路来解,是因为xj-xi<=bk,会发现它类似最短路中的三角不等式d[v] <=d[u]+w[u,v],即d[v]-d[u]<=w[u,v]。而求取最大值的过程类似于最短路算法中的松弛过程。
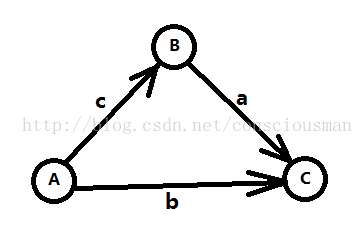
三角不等式:(在此引用大牛的博客)
B - A <= c (1)
C - B <= a (2)
C - A <= b (3)
如果要求C-A的最大值,可以知道max(C-A)= min(b,a+c),而这正对应了下图中C到A的最短路。
因此,对三角不等式加以推广,变量n个,不等式m个,要求xn-x1的最大值,便就是求取建图后的最短路。
同样地,如果要求取差分约束系统中xn-x1的最小值,便是求取建图后的最长路。最长路可以通过spfa求出来,只需要改下松弛的方向即可,即if(d[v] < d[u] + dist(u,v)) d[v] = d[u] + dist(u,v)。当然我们可以把图中所有的边权取负,求取最短路,两者是等价的。
最长路求解算法证明如下:
http://www.cnblogs.com/g0feng/archive/2012/09/13/2683880.html
最后一点,建图后不一定存在最短路/最长路,因为可能存在无限减小/增大的负环/正环,题目一般会对应于不同的输出。判断差分约束系统是否存在解一般判环即可。
3、差分约束系统的应用
差分约束系统的应用很广,都会有一定的背景,我们只需要根据题意构造出差分约束系统,然后再根据题目的要求求解就行了。
一般题目会有三种情况:(1)、求取最短路 (2)、求取最长路 (3)、判断差分约束系统的解是否存在
当然这三种也可能会相互结合。
差分约束系统的解法如下:
1、 根据条件把题意通过变量组表达出来得到不等式组,注意要发掘出隐含的不等式,比如说前后两个变量之间隐含的不等式关系。
2、 进行建图:
首先根据题目的要求进行不等式组的标准化。
(1)、如果要求取最小值,那么求出最长路,那么将不等式全部化成xi – xj >= k的形式,这样建立j->i的边,权值为k的边,如果不等式组中有xi – xj > k,因为一般题目都是对整形变量的约束,化为xi – xj >= k+1即可,如果xi – xj = k呢,那么可以变为如下两个:xi – xj >= k, xi – xj <= k,进一步变为xj – xi >= -k,建立两条边即可。
(2)、如果求取的是最大值,那么求取最短路,将不等式全部化成xi – xj <= k的形式, 这样建立j->i的边,权值为k的边,如果像上面的两种情况,那么同样地标准化就行了。
(3)、如果要判断差分约束系统是否存在解,一般都是判断环,选择求最短路或者最长路求解都行,只是不等式标准化时候不同,判环地话,用spfa即可,n个点中如果同一个点入队超过n次,那么即存在环。
值得注意的一点是:建立的图可能不联通,我们只需要加入一个超级源点,比如说求取最长路时图不联通的话,我们只需要加入一个点S,对其他的每个点建立一条权值为0的边图就联通了,然后从S点开始进行spfa判环。最短路类似。
3、 建好图之后直接spfa或bellman-ford求解,不能用dijstra算法,因为一般存在负边,注意初始化的问题。
本题中存在3种约束:第一种为牛的排列:d[i]<=d[i+1] ;
第二种为关系好的牛所限制的最大距离:d[AL] + DL >=d[BL];
第三种为关系差的牛限制的最小距离:d[AD] + DD <=d[BD]。
题目中求1号牛到n号牛的最大值,即求1到n的最短路。
变型不等式为最短路松弛形式操作得:d[i+1]+0 >= d[i] , d[AL]+DL >=d[BL] , d[BD]-DD >= d[AD]。
然后根据所有不等式建图,跑SPFA即可。
若SPFA过程中判出负环,则无解。
若结果最短路d[n] 为INF,则无约束,1到n的距离可以无限大。
代码:
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<map>
#include<stack>
#define sd(x) scanf("%d",&x)
#define ss(x) scanf("%s",x)
#define sc(x) scanf("%c",&x)
#define sf(x) scanf("%f",&x)
#define slf(x) scanf("%lf",&x)
#define slld(x) scanf("%lld",&x)
#define me(x,b) memset(x,b,sizeof(x))
#define pd(d) printf("%d\n",d);
#define plld(d) printf("%lld\n",d);
// #define Reast1nPeace
typedef long long ll;
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 10010;
int n,ml,md;
int k;
struct edge{
int to,weight,next;
}G[maxn*2];
int head[maxn];
int d[maxn];
bool vis[maxn];
int num[maxn];
void spfa(){
queue<int> q;
memset(d,INF,sizeof(d));
memset(num,0,sizeof(num));
memset(vis,0,sizeof(vis));
q.push(1);
vis[1] = 1;
d[1] = 0;
num[1]++;
while(!q.empty()){
int now = q.front(); q.pop();
for(int i = head[now] ; i!=0 ; i = G[i].next){
if(d[now] + G[i].weight < d[G[i].to] ){
d[G[i].to] = d[now]+G[i].weight;
if(!vis[G[i].to]){
q.push(G[i].to);
vis[G[i].to] = 1;
num[G[i].to]++;
if(num[G[i].to] >= n){
cout<<"-1"<<endl;
return;
}
}
}
}
vis[now] = 0;
}
if(d[n] == INF){
cout<<-2<<endl;
return;
}
cout<<d[n]<<endl;
}
int main(){
#ifdef Reast1nPeace
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
ios::sync_with_stdio(false);
memset(head,0,sizeof(head));
memset(G,0,sizeof(G));
cin>>n>>ml>>md;
int a,b,d;
k = 1;
for(int i = 2 ; i<=n ; i++){
G[k].to = i-1;
G[k].weight = 0;
G[k].next = head[i];
head[i] = k;
k++;
}
for(int i = 1 ; i<=ml ; i++){
cin>>a>>b>>d;
G[k].to = b;
G[k].weight = d;
G[k].next = head[a];
head[a] = k;
k++;
}
for(int i = 1 ; i<=md ; i++){
cin>>a>>b>>d;
G[k].to = a;
G[k].weight = -d;
G[k].next = head[b];
head[b] = k;
k++;
}
spfa();
return 0;
}







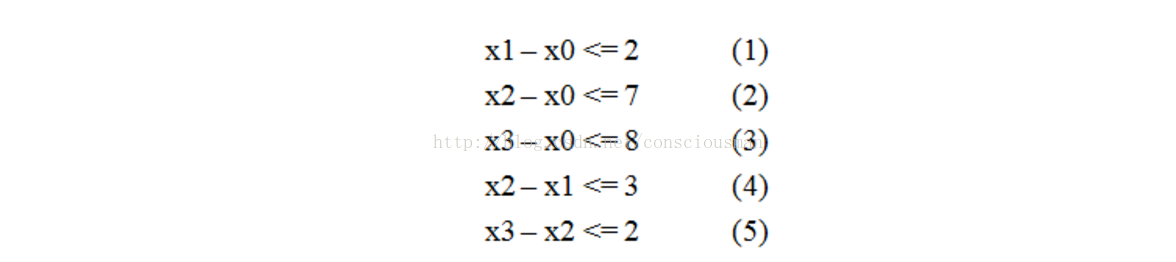














 3321
3321











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








