最近学习了splay的一些基本操作,写下这篇文章希望对初学者可以有所帮助~
Q:splay是什么?
A:他是一种二叉排序树,能在O(log n)的时间内完成插入、查找、删除、找结点的前驱后继、找区间第k大等的操作。他的一般操作都基于伸展操作【即splay(x),一会儿会说到】
Q:splay长什么样子?
A:首先他是一棵树,并且他是一棵二叉树;这棵树满足父亲节点的值大于左儿子,并且小于右儿子(等于可以自己定)。
现在,问题来了:splay的基本操作有哪些?怎么实现呢?
注:
1.我不太喜欢用指针。。所以代码全部用数组实现。
2.以下代码中a[i].fa表示父亲,a[i].size表示以i为根的子树的大小(包含i),a[i].l表示左儿子的结点编号,a[i].r表示右儿子的结点编号。
(一)zig zag操作
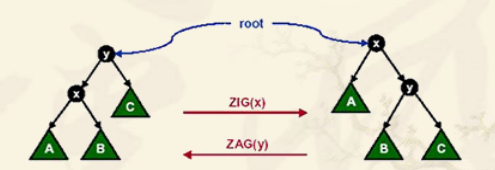
zig操作是将左儿子移到父亲节点,zag操作是将右儿子移到父亲节点。
为什么是这样转的呢?大家可以自己动手画一下。【注意这棵树满足左儿子<=父亲<右儿子的性质】
这里简要介绍一下zig操作:
x是y的左儿子,所以y比x大;当x成为y的父亲后,y就应该变成x的右儿子,那x的右儿子去哪里呢?
因为x的右儿子一定比y小,所以x的右儿子变成y的左儿子就可以,那么y的左儿子呢?
y的左儿子是x啊!
他已经成为y的父亲了,所以这样树就完成了zig(x)的旋转!
zag操作完全类似。
void update(int x) //zigzag后树的size就会改变,所以维护一下
{
a[x].size=a[a[x].l].size+a[a[x].r].size+1;
}
void zig(int x)
{
int y=a[x].fa;
int z=a[y].fa;
a[y].l=a[x].r,a[y].fa=x,a[x].fa=z;
a[a[x].r].fa=y;
a[x].r=y;
if (a[z].l==y) a[z].l=x;
else a[z].r=x; //写的时候要注意修改的顺序,否则有的结点你已经修改过了但是你却想用的是修改前的数据
update(y);
update(x);
}
void zag(int x)
{
int y=a[x].fa;
int z=a[y].fa;
a[y].r=a[x].l,a[x].fa=z,a[y].fa=x;
a[a[x].l].fa=y;
a[x].l=y;
if (a[z].l==y) a[z].l=x;
else a[z].r=x;
update(y);
update(x);
}
(二)splay操作(关键!!)
splay(x)就是把x旋转到根节点。
在旋转的过程中要分三种情况处理:
(1)zig(x)或zag(x):此时x已经是根节点的儿子,只要旋转一次就可以达到目的。
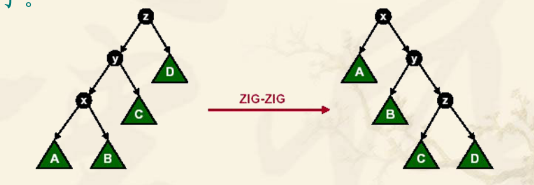
(2)zig(y)-zig(x)或zag(y)-zag(x)(一字型旋转):x为y的左儿子,y为z父亲的左儿子。那么现将y旋转到z(此时x仍然为y的左儿子),再将x旋转到y。
(反之同理)
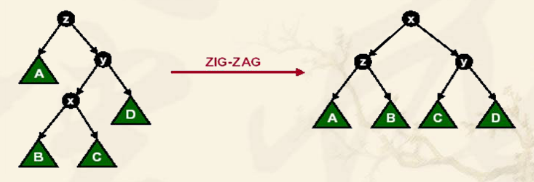
(3)zig(x)-zag(x)或zag(x)-zig(x)(之字型旋转):x为y的左儿子,y为z的右儿子。那么先将x旋转到y,再将y旋转到z。
为什么不能zag(y)-zig(x)?因为把y旋转到z后,y的左儿子变成了z,此时再旋转就会出错。
(反之同理)
但是!!为什么一定要双旋?每次只旋转一个点不可以吗?
不可以!!如果当前的树是一个长度为n的链,将最下面的旋转到根结点要旋转n-1次,并且旋转完成后仍是一条链,最终时间复杂度变成O(nm)了!因此双旋虽然比单旋要难写一点,但是能够保证树的平衡(深度为logn左右),从而保证时间复杂度。
void splay(int x)
{
while (a[x].fa)
{
int y=a[x].fa;
int z=a[y].fa;
if (!z) //第一种情况
{
if (a[y].l==x) zig(x);
else zag(x);
break;
}
else
{
if (y==a[z].l) //第二种情况
{
if (x==a[y].l) zig(y),zig(x);
else zag(x),zig(x);
}
else //第三种情况
{
if (x==a[y].r) zag(y),zag(x);
else zig(x),zag(x);
}
}
}
root=x; //注意最后不要忘了root变成了x
}
(三)search操作
search(w)是为了方便下文的insert(w):找w在树中应该插入到哪个结点的儿子。(当然稍作修改就可以变成查询w这个值所在的位置)
方法是从根节点开始,如果w小于根结点的值,那么顺着这左子树继续找,否则顺着右子树继续找。
int search(int w)
{
int x=root,p; //p就是所求的位置
while (x)
{
p=x;
if (a[x].data>=w) x=a[x].l;
else x=a[x].r;
}
return p;
}
(四)insert操作
insert(w)就是把值为w的数插入到树中。
分两种情况讨论:
(1)当前根是0,即树中没有结点:直接把这个值插到根结点下
(2)当前树中有结点:先search(w)(见上文),然后如果w大于找到的结点的值,把w作为右儿子,反之同理。最后一定要记住把插入的w旋转到根结点。
为什么一定要旋转到根结点?因为你插入一个数之后,与他相关的结点的size值就会改变,而splay操作可以将修改update,使整棵树维护的数据不会出错。
<pre name="code" class="cpp">void insert(int w)
{
if (root==0) //第一种情况
{
a[++tot].fa=0,a[tot].size=1,a[tot].data=w,root=tot;
return;
}
int i=search(w); //第二种情况
tot++;
a[tot].data=w,a[tot].fa=i,a[tot].size=1;
if (a[i].data>=w) a[i].l=tot;
else a[i].r=tot;
splay(tot);
}(五)delete操作
delete(k)表示删除树中小于k的所有值。
方法是插入一个k值,并把他旋转到根结点,然后直接把root赋值为a[root].r,此时就把小于k的树全部“砍”掉了。
void delete(int k)
{
insert(k);
root=a[root].r;
a[root].fa=0;
}
(六)findkth操作
寻找第k大的数。
方法是通过每个结点的size递归寻找即可,分三种情况:
(1)当前的结点x就是第k个数,直接返回当前结点的值
(2)第k个数在左子树中,递归寻找左子树中第k大的值
(3)第k个数在右子树中,递归寻找右子树中第(k-1-a[a[x].l].size大的值)
int findkth(int x,int k)
{
if (k==a[a[x].l].size+1) return a[x].data; //第一种情况
if (k<=a[a[x].l].size) return findkth(a[x].l,k); //第二种情况
else return findkth(a[x].r,k-1-a[a[x].l].size); //第三种情况
}
本文的操作都是基于bzoj1503[noi2004]郁闷的出纳员 来写的,下面贴上本题完整代码。大家可以用这道题作为自己的splay第一题,练习基本操作。
1503: [NOI2004]郁闷的出纳员
Time Limit: 5 Sec Memory Limit: 64 MBSubmit: 6373 Solved: 2229
[ Submit][ Status]
Description
OIER公司是一家大型专业化软件公司,有着数以万计的员工。作为一名出纳员,我的任务之一便是统计每位员工的工资。这本来是一份不错的工作,但是令人郁闷的是,我们的老板反复无常,经常调整员工的工资。如果他心情好,就可能把每位员工的工资加上一个相同的量。反之,如果心情不好,就可能把他们的工资扣除一个相同的量。我真不知道除了调工资他还做什么其它事情。工资的频繁调整很让员工反感,尤其是集体扣除工资的时候,一旦某位员工发现自己的工资已经低于了合同规定的工资下界,他就会立刻气愤地离开公司,并且再也不会回来了。每位员工的工资下界都是统一规定的。每当一个人离开公司,我就要从电脑中把他的工资档案删去,同样,每当公司招聘了一位新员工,我就得为他新建一个工资档案。老板经常到我这边来询问工资情况,他并不问具体某位员工的工资情况,而是问现在工资第k多的员工拿多少工资。每当这时,我就不得不对数万个员工进行一次漫长的排序,然后告诉他答案。好了,现在你已经对我的工作了解不少了。正如你猜的那样,我想请你编一个工资统计程序。怎么样,不是很困难吧?
Input

Output
输出文件的行数为F命令的条数加一。对于每条F命令,你的程序要输出一行,仅包含一个整数,为当前工资第k多的员工所拿的工资数,如果k大于目前员工的数目,则输出-1。输出文件的最后一行包含一个整数,为离开公司的员工的总数。
Sample Input
I 60
I 70
S 50
F 2
I 30
S 15
A 5
F 1
F 2
Sample Output
20
-1
2
HINT
I命令的条数不超过100000 A命令和S命令的总条数不超过100 F命令的条数不超过100000 每次工资调整的调整量不超过1000 新员工的工资不超过100000
Source
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
using namespace std;
struct node
{
int l,r,size,data,fa;
}a[1000000];
int n,m,temp=0,ans=0;
int tot=0,root;
void update(int x)
{
a[x].size=a[a[x].l].size+a[a[x].r].size+1;
}
void zig(int x)
{
int y=a[x].fa;
int z=a[y].fa;
a[y].l=a[x].r,a[y].fa=x,a[x].fa=z;
a[a[x].r].fa=y;
a[x].r=y;
if (a[z].l==y) a[z].l=x;
else a[z].r=x;
update(y);
update(x);
}
void zag(int x)
{
int y=a[x].fa;
int z=a[y].fa;
a[y].r=a[x].l,a[x].fa=z,a[y].fa=x;
a[a[x].l].fa=y;
a[x].l=y;
if (a[z].l==y) a[z].l=x;
else a[z].r=x;
update(y);
update(x);
}
void splay(int x)
{
while (a[x].fa)
{
int y=a[x].fa;
int z=a[y].fa;
if (!z)
{
if (a[y].l==x) zig(x);
else zag(x);
break;
}
else
{
if (y==a[z].l)
{
if (x==a[y].l) zig(y),zig(x);
else zag(x),zig(x);
}
else
{
if (x==a[y].r) zag(y),zag(x);
else zig(x),zag(x);
}
}
}
root=x;
}
int search(int w)
{
int x=root,an;
while (x)
{
an=x;
if (a[x].data>=w) x=a[x].l;
else x=a[x].r;
}
return an;
}
void insert(int w)
{
if (root==0)
{
a[++tot].fa=0,a[tot].size=1,a[tot].data=w,root=tot;
return;
}
int i=search(w);
tot++;
a[tot].data=w,a[tot].fa=i,a[tot].size=1;
if (a[i].data>=w) a[i].l=tot;
else a[i].r=tot;
splay(tot);
}
void delet(int k)
{
insert(k);
root=a[root].r;
a[root].fa=0;
}
int findkth(int x,int k)
{
if (k==a[a[x].l].size+1) return a[x].data;
if (k<=a[a[x].l].size) return findkth(a[x].l,k);
else return findkth(a[x].r,k-1-a[a[x].l].size);
}
int main()
{
scanf("%d%d",&n,&m);
while (n--)
{
char c;
int t;
scanf("%s %d",&c,&t);
if (c=='I'&&t>=m)
insert(t-temp),ans++;
if (c=='A')
temp+=t;
if (c=='S')
temp-=t,delet(m-temp);
if (c=='F')
{
if (t>a[root].size) printf("-1\n");
else
{
printf("%d\n",findkth(root,a[root].size-t+1)+temp);
}
}
}
printf("%d\n",ans-a[root].size);
return 0;
}
如果对本文有疑问或者有修改意见的欢迎在文章下面发表评论~
参考:
杨思雨《伸展树的基本操作和应用》






















 439
439

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








