代码随想录刷题记录-21 动态规划（5）习题

Renas_TJOvO

于 2024-08-30 23:30:00 发布

阅读量1.1k

点赞数 39

文章标签：动态规划算法

本文链接：https://blog.csdn.net/Renas_TJOvO/article/details/141613350

版权

1.198.打家劫舍

动规五部曲：

1.dp数组及下标i的含义

dp[i] : 考虑下标i以内的房屋，所能盗取的最大金额为dp[i]

2.递推公式

决定dp[i]的因素就是第i房间偷还是不偷。

如果偷：dp[i] = dp[i-2] + nums[i]

如果不偷：dp[i] = dp[i-1] （这里是考虑下标为i-1的房屋，不是偷下标为i-1的房屋）

dp[i] = Math.max(dp[i-2] + nums[i] , dp[i-1])

3.初始化

从递推公式上看，dp依赖于 dp[0] 和 dp[1]

从定义上，dp[0] = nums[0]

dp[1] = Math.max(dp[0], dp[1])

4.确定遍历顺序

从递推公式上看，所求元素依赖于它前面的，正序遍历。

5.dp模拟

以示例二，输入[2,7,9,3,1]为例。

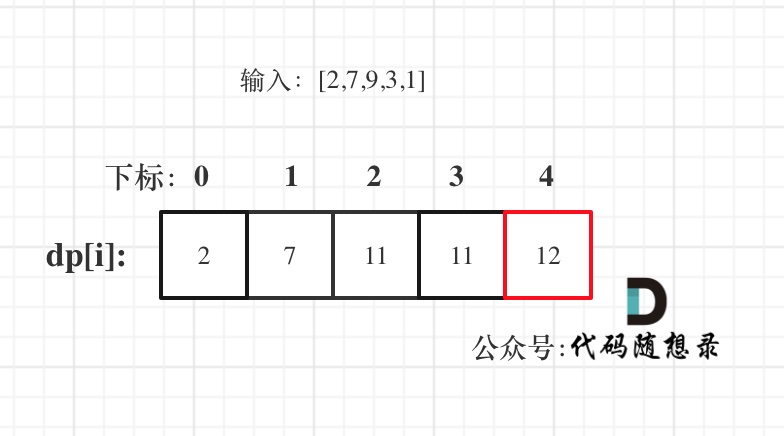
198.打家劫舍

class Solution {
    public int rob(int[] nums) {
        if(nums.length == 1) return nums[0];
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        dp[1] = Math.max(nums[0],nums[1]);
        for(int i = 2; i < nums.length ; i++){
            dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i]);
        }
        return dp[nums.length-1];
    }
}

2.213.打家劫舍II

这道题目和198.打家劫舍是差不多的，唯一区别就是成环了。

第一家和最后一家不能同时抢劫，希望把环线性化。

线性化成两种情况：不考虑第一家和不考虑最后一家。

得到两个结果，由于第一家和最后一家不能够同时选择，这两种情况实际上涵盖了环形的所有情况。

代码如下：

class Solution {
    int[] nums;
    public int rob(int[] nums) {
        this.nums = nums;
        if(nums.length == 1) return nums[0];
        int result1 = rob2(0,nums.length-2);
        int result2 = rob2(1,nums.length-1);
        return Math.max(result1,result2);
    }
    
    public int rob2(int start , int end){
        //左闭右闭
        int[] dp = new int[nums.length-1];
        if(nums.length-1 == 1) return nums[start];
        dp[0] = nums[start];
        dp[1] = Math.max(nums[start],nums[start+1]);
        start +=2;
        for(int i = 2 ;i < nums.length - 1 ; i++,start++){
            dp[i] = Math.max(dp[i-1],dp[i-2] + nums[start]);
        }
        return dp[nums.length-2];
    }
}

3.337.打家劫舍 III

对于树，首先想到遍历方式。本题一定是要后序遍历，因为通过递归函数的返回值来做下一步计算。

与198.打家劫舍，213.打家劫舍II一样，关键是要讨论当前节点抢还是不抢。

如果抢了当前节点，两个孩子就不能动，如果没抢当前节点，就可以考虑抢左右孩子（注意这里说的是“考虑”）

暴力递归

代码如下：

class Solution {
public:
    int rob(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right == NULL) return root->val;
        // 偷父节点
        int val1 = root->val;
        if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 跳过root->left，相当于不考虑左孩子了
        if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 跳过root->right，相当于不考虑右孩子了
        // 不偷父节点
        int val2 = rob(root->left) + rob(root->right); // 考虑root的左右孩子
        return max(val1, val2);
    }
};

以上代码超时了，这个递归的过程中其实是有重复计算了。

我们计算了root的四个孙子（左右孩子的孩子）为头结点的子树的情况，又计算了root的左右孩子为头结点的子树的情况，计算左右孩子的时候其实又把孙子计算了一遍。

记忆化递推

所以可以使用一个map把计算过的结果保存一下，这样如果计算过孙子了，那么计算孩子的时候可以复用孙子节点的结果。

代码如下：

class Solution {
public:
    unordered_map<TreeNode* , int> umap; // 记录计算过的结果
    int rob(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right == NULL) return root->val;
        if (umap[root]) return umap[root]; // 如果umap里已经有记录则直接返回
        // 偷父节点
        int val1 = root->val;
        if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 跳过root->left
        if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 跳过root->right
        // 不偷父节点
        int val2 = rob(root->left) + rob(root->right); // 考虑root的左右孩子
        umap[root] = max(val1, val2); // umap记录一下结果
        return max(val1, val2);
    }
};

时间复杂度：O(n)
空间复杂度：O(log n)，算上递推系统栈的空间

动态规划

在上面两种方法，其实对一个节点偷与不偷得到的最大金钱都没有做记录，而是需要实时计算。

动态规划其实就是使用状态转移容器来记录状态的变化，这里可以使用一个长度为2的数组，记录当前节点偷与不偷所得到的的最大金钱。

这道题目算是树形dp的入门题目，因为是在树上进行状态转移，在讲解二叉树的时候说过递归三部曲，那么下面我以递归三部曲为框架，其中融合动规五部曲的内容来进行讲解。

1.确定递归函数参数和返回值

要求一个节点偷与不偷的两个状态所得到的金钱，那么返回值就是一个长度为2的数组

参数为当前节点，代码如下：

vector<int> robTree(TreeNode* cur) {

这里的返回数组就是dp数组。

所以dp数组（dp table）以及下标的含义：下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。

所以本题dp数组就是一个长度为2的数组。

在递归的过程中，系统栈会保存每一层递归的参数。

2.确定终止条件

在遍历的过程中，如果遇到空节点的话，很明显，无论偷还是不偷都是0，所以就返回

if (cur == NULL) return vector<int>{0, 0};

相当于dp数组的初始化

3.确定遍历顺序

明确的是使用后序遍历。因为要通过递归函数的返回值来做下一步计算。

通过递归左节点，得到左节点偷与不偷的金钱。

通过递归右节点，得到右节点偷与不偷的金钱。

代码如下：

// 下标0：不偷，下标1：偷
vector<int> left = robTree(cur->left); // 左
vector<int> right = robTree(cur->right); // 右
// 中

4.确定单层递归逻辑

如果偷当前节点，就不能考虑偷左右孩子节点

int val1 = root.val + left[0] + right[0]

如果不偷当前节点，就可以考虑偷左右孩子结点

int val2 = Math.max(left[0], left[1]) + Math.max(right[0] , right[1])

return new int[] { val2,val1};

代码如下：

vector<int> left = robTree(cur->left); // 左
vector<int> right = robTree(cur->right); // 右

// 偷cur
int val1 = cur->val + left[0] + right[0];
// 不偷cur
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};

5.dp模拟

以示例1为例，dp数组状态如下：（注意用后序遍历的方式推导）

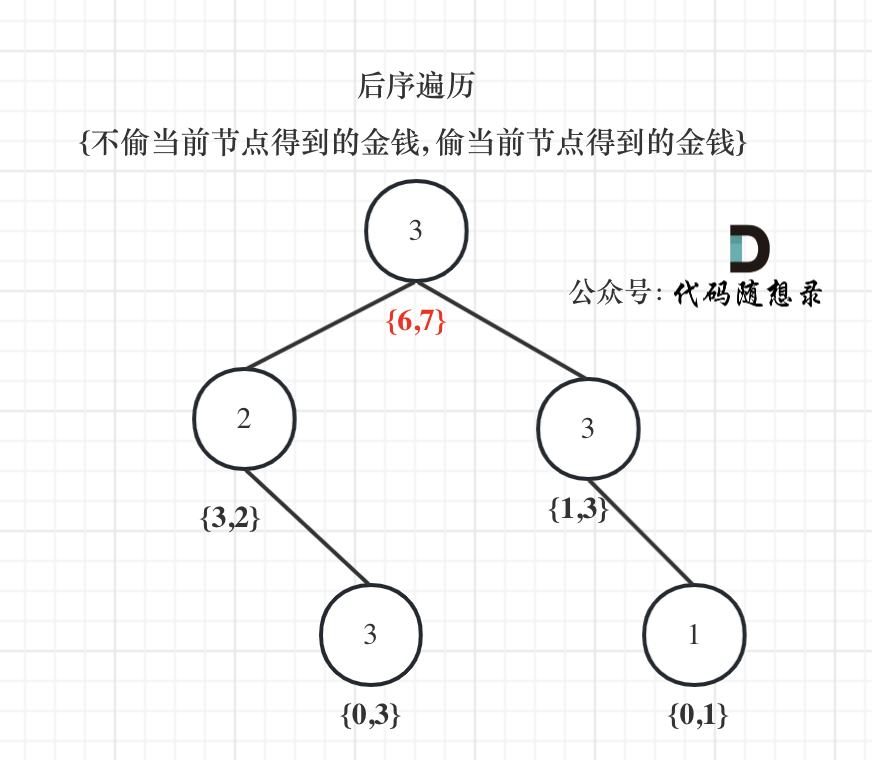
最后头结点就是取下标0 和下标1的最大值就是偷得的最大金钱。

时间复杂度：O(n)，每个节点只遍历了一次
空间复杂度：O(log n)，算上递推系统栈的空间

总结

这道题是树形DP的入门题目，所谓树形DP就是在树上进行递归公式的推导。

只不过平时我们习惯了在一维数组或者二维数组上推导公式，一下子换成了树，就需要对树的遍历方式足够了解。

4.121. 买卖股票的最佳时机

思路

暴力

class Solution {
    public int maxProfit(int[] prices) {
        int maxProfit = 0;
        for(int i = 0 ; i < prices.length ; i++){
            for(int j = i+1 ; j < prices.length ; j++){
                maxProfit = Math.max(maxProfit,prices[j] - prices[i]);
            }
        }
        return maxProfit;
    }
}

会时间超限

贪心

贪心策略：

局部最优：当前价格和左边价格的最大差值

全局最优：最大利润

class Solution {
    public int maxProfit(int[] prices) {
        int low = Integer.MAX_VALUE;
        int result = 0;
        for(int i = 0 ; i < prices.length ; i++){
            low = Math.min(low,prices[i]);
            result = Math.max(result,prices[i]-low);
        }
        return result;
    }
}

动态规划

动规五部曲:

1. 确定dp数组（dp table）以及下标的含义

dp[i][0] : 第i天持有股票，所持有的最多现金是 dp[i][0]

一开始现金是0，那么加入第i天买入股票现金就是 -prices[i]，这是一个负数。

dp[i][1]：第i天不持有股票，所持有的现金是dp[i][1]

持有”不代表就是当天“买入”,也有可能是昨天就买入了，今天保持持有的状态。

2.确定递推公式

dp[i][0]有两种可能，第i-1天就持有股票，第i天保持；或者第i天买入。

（由于本题只能够买入1次，所以第i天买入只能是第一次买入，而不能从dp[i-1][1]计算，利润为

-prices[i]

dp[i][0] = Math.max(dp[i-1][0] , - prices[i] )

dp[i][1]有两种可能，第i-1天就不持有股票，第i天保持；或者第i-1天持有股票，第i天卖出。

dp[i][1] = Math.max(dp[i-1][1], dp[i-1][1] + prices[i] )

3.遍历顺序

根据递推公式，后面的依赖于前面的，正序遍历

4.初始化

根据递推公式，dp元素的值依赖于dp[0][0]和dp[0][1]

根据dp数组及下标定义

dp[0][0] = - prices[0];

dp[0][1] = 0;

5.dp模拟

以示例1，输入：[7,1,5,3,6,4]为例，dp数组状态如下：

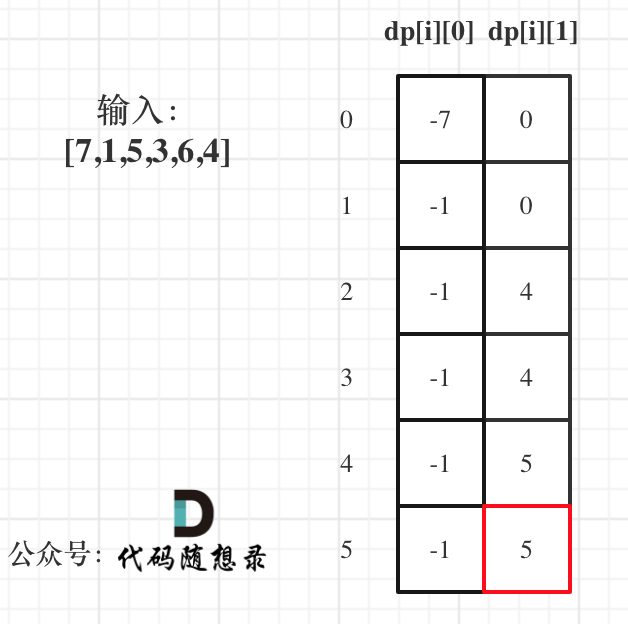
121.买卖股票的最佳时机

最后的结果是dp[prices.length-1][1] ，这是因为在本题中，不持有股票所持有的现金一定比持有股票多。也可以举一个简单的例子，会发现是结果是dp[prices.length-1][1].

从递推公式可以看出，dp[i]只是依赖于dp[i - 1]的状态。

dp[i][0] = max(dp[i - 1][0], -prices[i]);
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

那么我们只需要记录当前天的dp状态和前一天的dp状态就可以了，可以使用滚动数组来节省空间，代码如下：

class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[2][2];
        dp[0][0] = - prices[0];
        dp[0][1] = 0;
        for(int i = 1; i < prices.length ; i++){
            dp[i%2][0] = Math.max(dp[(i-1)%2][0], - prices[i]);
            dp[i%2][1] = Math.max(dp[(i-1)%2][1],dp[(i-1)%2][0] + prices[i]);
        }
        return dp[(prices.length-1)%2][1];
    }
}

5.122.买卖股票的最佳时机II

思路

贪心

局部最优：有正利润，就操作

全局最优：最大利润

所有正利润求和 ->最大利润

代码如下：

class Solution {
    public int maxProfit(int[] prices) {
        int sum = 0;
        int pre = 0; 
        int cur = 0;
        for(int i = 0 ; i < prices.length-1 ; i++){
            cur = prices[i+1] - prices[i];
            if(cur > 0) sum += cur;
            pre = cur;
        }
        return sum;
    }
}

动态规划

本题和121. 买卖股票的最佳时机的唯一区别是本题股票可以买卖多次了（注意只有一只股票，所以再次购买前要出售掉之前的股票）

那么与之前相比，递推公式不同，其余基本相同：

动规五部曲:

1. 确定dp数组（dp table）以及下标的含义

dp[i][0] : 第i天持有股票，所持有的最多现金是 dp[i][0]

一开始现金是0，那么加入第i天买入股票现金就是 -prices[i]，这是一个负数。

dp[i][1]：第i天不持有股票，所持有的现金是dp[i][1]

持有”不代表就是当天“买入”,也有可能是昨天就买入了，今天保持持有的状态。

2.确定递推公式

dp[i][0]有两种可能，第i-1天就持有股票，第i天保持；或者第i天买入。

因为一只股票可以买卖多次，所以当第i天买入股票的时候，所持有的现金可能有之前买卖过的利润：

dp[i][0] = Math.max(dp[i-1][0] , dp[i-1][1]- prices[i] )

dp[i][1]有两种可能，第i-1天就不持有股票，第i天保持；或者第i-1天持有股票，第i天卖出。

dp[i][1] = Math.max(dp[i-1][1], dp[i-1][1] + prices[i] )

3.遍历顺序

根据递推公式，后面的依赖于前面的，正序遍历

4.初始化

根据递推公式，dp元素的值依赖于dp[0][0]和dp[0][1]

根据dp数组及下标定义

dp[0][0] = - prices[0];

dp[0][1] = 0;

5.dp模拟

代码如下：

public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][2];
        dp[0][0] = - prices[0];
        dp[0][1] = 0;
        for(int i = 1; i < prices.length ; i++){
            dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
        }
        return dp[prices.length-1][1];
    }

滚动数组优化：

public int maxProfit(int[] prices) {
        int[][] dp = new int[2][2];
        dp[0][0] = - prices[0];
        dp[0][1] = 0;
        for(int i = 1; i < prices.length ; i++){
            dp[i%2][0] = Math.max(dp[(i-1)%2][0], dp[(i-1)%2][1]- prices[i]);
            dp[i%2][1] = Math.max(dp[(i-1)%2][1],dp[(i-1)%2][0] + prices[i]);
        }
        return dp[(prices.length-1)%2][1];
    }

6.123.买卖股票的最佳时机III

这道题关键在于至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。

动态规划五部曲：

1.dp数组及下标含义

一天一共就有五个状态，

0.没有操作（其实我们也可以不设置这个状态）

1.第一次持有股票

2.第一次不持有股票

3.第二次持有股票

4.第二次不持有股票

dp[i][j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j]表示第i天状态j所剩最大现金为dp[i][j]。

需要注意：dp[i][1]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，有可能第 i-1天就买入了，那么 dp[i][1] 延续买入股票的这个状态。

2.递推公式

达到dp[i][1]状态，有两个具体操作：

操作一：第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i]
操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]

dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);

同理dp[i][2]也有两个操作：

操作一：第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]

dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])

同理有：

dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);

dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);

3.初始化

第0天没有任何操作，则利润0，dp[0][0]=0;

第0天第一次买入，则dp[0][1] = - price[i];

第0天做第一次卖出的操作，这个初始值应该是多少呢？

此时还没有买入，怎么就卖出呢？可以理解成当天买入，当天卖出，所以dp[0][2] = 0;

第0天第二次买入操作,依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：dp[0][3] = -prices[0];

同理第二次卖出初始化dp[0][4] = 0;

4.遍历顺序

正序遍历，因为dp[i]，依靠dp[i - 1]的数值。

5.dp模拟

以输入[1,2,3,4,5]为例

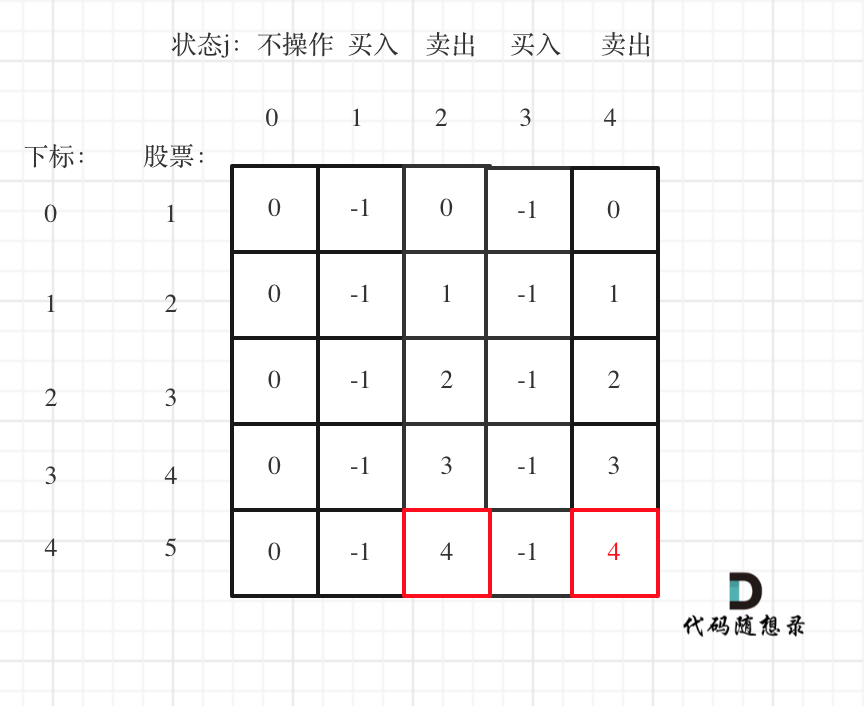
123.买卖股票的最佳时机III

可以看到红色框为最后两次卖出的状态。

现在最大的时候一定是卖出的状态，而两次卖出的状态现金最大一定是最后一次卖出。如果想不明白的录友也可以这么理解：如果第一次卖出已经是最大值了，那么我们可以在当天立刻买入再立刻卖出。所以dp[4][4]已经包含了dp[4][2]的情况。也就是说第二次卖出手里所剩的钱一定是最多的。

所以最终最大利润是dp[4][4]。

代码如下：

class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][5];
        //0:不操作
        //1:第一次买入
        //2:第一次卖出
        //3:第二次买入
        //4:第二次卖出
        dp[0][0] = 0;
        dp[0][1] = - prices[0];
        dp[0][2] = 0;
        dp[0][3] = - prices[0];
        dp[0][4] = 0;
        for(int i = 1 ; i < prices.length ; i++){
            dp[i][0] = dp[i-1][0];
            dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] - prices[i]);
            dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1] + prices[i]);
            dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2] - prices[i]);
            dp[i][4] = Math.max(dp[i-1][4],dp[i-1][3] + prices[i]);;
        }
        return dp[prices.length-1][4];

    }
}

空间优化，C++版本：

// 版本二
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<int> dp(5, 0);
        dp[1] = -prices[0];
        dp[3] = -prices[0];
        for (int i = 1; i < prices.size(); i++) {
            dp[1] = max(dp[1], dp[0] - prices[i]);
            dp[2] = max(dp[2], dp[1] + prices[i]);
            dp[3] = max(dp[3], dp[2] - prices[i]);
            dp[4] = max(dp[4], dp[3] + prices[i]);
        }
        return dp[4];
    }
};

dp[2]利用的是当天的dp[1]。但结果也是对的。

我来简单解释一下：

dp[1] = max(dp[1], dp[0] - prices[i]); 如果dp[1]取dp[1]，即保持买入股票的状态，那么 dp[2] = max(dp[2], dp[1] + prices[i]);中dp[1] + prices[i] 就是今天卖出。

如果dp[1]取dp[0] - prices[i]，今天买入股票，那么dp[2] = max(dp[2], dp[1] + prices[i]);中的dp[1] + prices[i]相当于是今天再卖出股票，一买一卖收益为0，对所得现金没有影响。相当于今天买入股票又卖出股票，等于没有操作，保持昨天卖出股票的状态了。

这种写法看上去简单，其实思路很绕，不建议大家这么写，这么思考，很容易把自己绕进去！

拓展

其实我们可以不设置，‘0. 没有操作’ 这个状态，因为没有操作，手上的现金自然就是0（全部都是0，可以用0替代），正如我们在 121.买卖股票的最佳时机 (opens new window)和 122.买卖股票的最佳时机II (opens new window)也没有设置这一状态是一样的。

代码如下：

// 版本三 
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
        dp[0][1] = -prices[0];
        dp[0][3] = -prices[0];
        for (int i = 1; i < prices.size(); i++) {
            dp[i][1] = max(dp[i - 1][1], 0 - prices[i]);
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.size() - 1][4];
    }
};

总结

本题的难点在于状态更加多样，需要考虑周全，表示好状态，进而推得递推公式。

7.188.买卖股票的最佳时机IV

本题把状态推广到 2*k+1种（不考虑什么也没做的话就是2*k）

动规五部曲，分析如下：

1.确定dp数组以及下标的含义

使用二维数组 dp[i][j] ：第i天的状态为j，所剩下的最大现金是dp[i][j]

j的状态表示为：j=0，不操作，除了0以外，偶数就是卖出，奇数就是买入。

2.递推公式

for (int j = 0; j < 2 * k - 1; j += 2) {
    dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
    dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}

3.初始化

第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0;

第0天做第一次买入的操作，dp[0][1] = -prices[0];

第0天做第一次卖出的操作，这个初始值应该是多少呢？

此时还没有买入，怎么就卖出呢？其实大家可以理解当天买入，当天卖出，所以dp[0][2] = 0;

第0天第二次买入操作，初始值应该是多少呢？应该不少同学疑惑，第一次还没买入呢，怎么初始化第二次买入呢？

第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后在买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：dp[0][3] = -prices[0];

第二次卖出初始化dp[0][4] = 0;

所以同理可以推出dp[0][j]当j为奇数的时候都初始化为 -prices[0]

代码如下：

for (int j = 1; j < 2 * k; j += 2) {
    dp[0][j] = -prices[0];
}

在初始化的地方同样要类比j为偶数是卖、奇数是买的状态。

4.遍历顺序

根据递推公式，dp[i] 要依赖于 dp[i-1],正序遍历

5.dp模拟

以输入[1,2,3,4,5]，k=2为例。

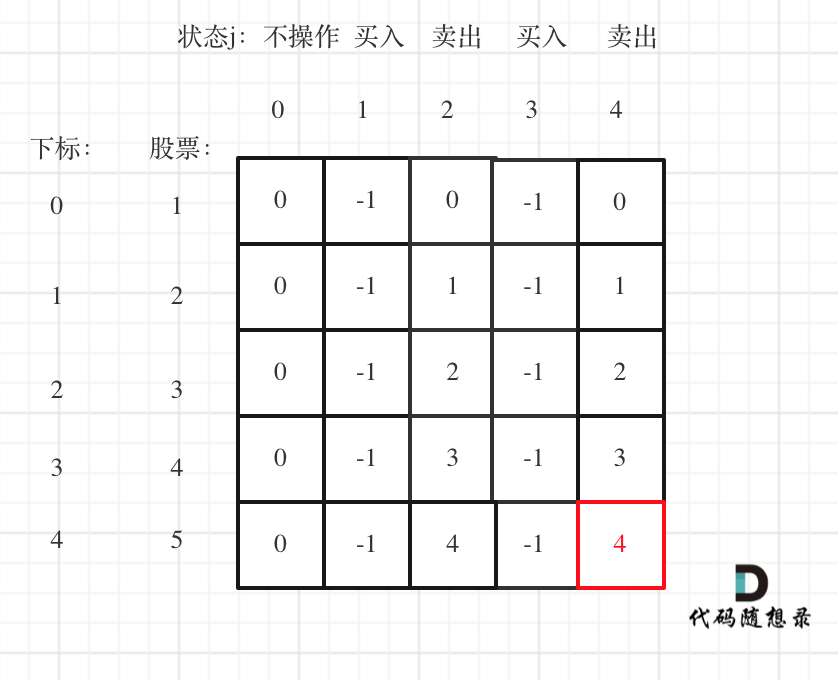
188.买卖股票的最佳时机IV

最后一次卖出，一定是利润最大的，dp[prices.size() - 1][2 * k]即红色部分就是最后求解。

代码如下：

class Solution {
    public int maxProfit(int k, int[] prices) {
        int[][] dp = new int[prices.length][k*2+1];
        for(int i = 1; i <= k*2 ; i++){
            if(i%2 == 1){
                dp[0][i] = -prices[0];
            }
        }
        for(int i = 1 ; i < prices.length ; i++){
            dp[i][0] = dp[i-1][0];
            for(int j = 1 ; j <= 2*k ; j++){
                if(j%2==1){
                    dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-1] - prices[i]);
                }else{
                    dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-1] + prices[i]);
                }
            }
        }

        return dp[prices.length-1][k*2];
    }
}

8.309.最佳买卖股票时机含冷冻期

动规五部曲，分析如下：

1.确定dp数组以及下标的含义

dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]。

具体可以区分出如下四个状态：

状态一：持有股票状态（今天买入股票，或者是之前就买入了股票然后没有操作，一直持有）
不持有股票状态
- 状态二：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）
- 状态三：今天卖出股票
- 状态四：冷冻期状态

j的状态为：

0：状态一
1：状态二
2：状态三
3：状态四

2.递推公式

达到买入股票状态（状态一）即：dp[i][0]，有两个具体操作：

操作一：前一天就是持有股票状态（状态一），dp[i][0] = dp[i - 1][0]
操作二：今天买入了，有两种情况
- 前一天是冷冻期（状态四），dp[i - 1][3] - prices[i]
- 前一天是保持卖出股票的状态（状态二），dp[i - 1][1] - prices[i]

那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);

达到保持卖出股票状态（状态二）即：dp[i][1]，有两个具体操作：

操作一：前一天就是状态二
操作二：前一天是冷冻期（状态四）

dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);

达到今天就卖出股票状态（状态三），即：dp[i][2] ，只有一个操作：

昨天一定是持有股票状态（状态一），今天卖出

即：dp[i][2] = dp[i - 1][0] + prices[i];

达到冷冻期状态（状态四），即：dp[i][3]，只有一个操作：

昨天卖出了股票（状态三）

dp[i][3] = dp[i - 1][2];

综上分析，递推代码如下：

dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];

3.dp数组初始化

如果是持有股票状态（状态一）那么：dp[0][0] = -prices[0]，一定是当天买入股票。

保持卖出股票状态（状态二），这里其实从「状态二」的定义来说，很难明确应该初始多少，这种情况我们就看递推公式需要我们给他初始成什么数值。

如果i为1，第1天买入股票，那么递归公式中需要计算 dp[i - 1][1] - prices[i] ，即 dp[0][1] - prices[1]，那么大家感受一下 dp[0][1] （即第0天的状态二）应该初始成多少，只能初始为0。想一想如果初始为其他数值，是我们第1天买入股票后手里还剩的现金数量是不是就不对了。

今天卖出了股票（状态三），同上分析，dp[0][2]初始化为0，dp[0][3]也初始为0。

4.遍历顺序

正序遍历

5.dp模拟

以 [1,2,3,0,2] 为例，dp数组如下：

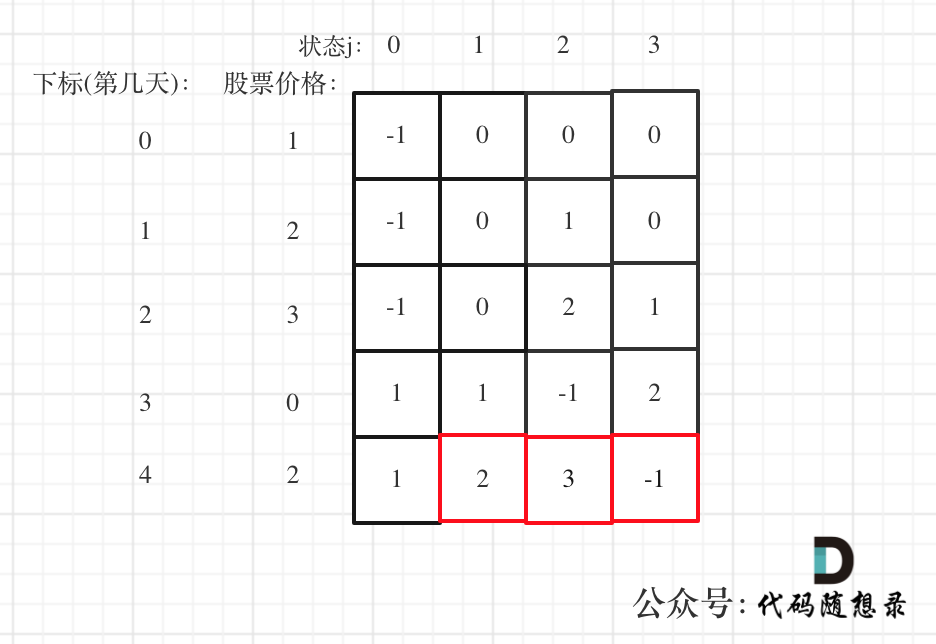
309.最佳买卖股票时机含冷冻期

最后结果是取状态二，状态三，和状态四的最大值。

代码如下：

class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][4];
        dp[0][0] = - prices[0];
        //0:持有
        //1:不持有，非卖出，非冷冻期
        //2:不持有，卖出
        //3:不持有，冷冻期
        for(int i = 1 ; i < prices.length ; i++){
            dp[i][0] = Math.max(dp[i-1][0],Math.max(dp[i-1][1] - prices[i],dp[i-1][3] - prices[i]));
            dp[i][1] = Math.max(dp[i-1][1],dp[i-1][3]);
            dp[i][2] = dp[i-1][0] + prices[i];
            dp[i][3] = dp[i-1][2];
        }
        return Math.max(dp[prices.length-1][1],Math.max(dp[prices.length-1][2],dp[prices.length-1][3]));
    }
}

总结：

本题复杂在状态的划分，并基于此推出递推方程。

打家劫舍思想，简化为两个状态：

如果当前是持有状态，那么来源于昨天的持有状态，或前天不持有状态-prices[i]

如果当前不持有状态，那么来源于昨天的不持有状态，或昨天的持有状态 + prices[i]

1.dp数组下标及含义

dp[i][j]：表示第i天状态j下所持有的最多现金数量

2.递推方程

dp[i][0] = Math.max(dp[i-1][0] ,dp[i-2][1] - prices[i]);

dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);

3.初始化

dp[0][0] = - prices[0];

dp[0][1] = 0;

dp[1][0] = Math.max(dp[0][0] , - prices[1])

dp[1][1] = Math.max(dp[0][1], dp[0][0] +prices[1])

4.遍历顺序

根据递推方程，后面的依赖于前面的，正序遍历

5.dp模拟

class Solution {
    public int maxProfit(int[] prices) {
        //0: 持有
        //1:卖出
        if(prices.length == 1) return 0;
        int[][] dp = new int[prices.length][2];
        dp[0][0] = - prices[0];
        dp[0][1] = 0;
        dp[1][0] = Math.max(dp[0][0],dp[0][1] - prices[1]);
        dp[1][1] = Math.max(dp[0][1],dp[0][0] + prices[1]);
        for(int i = 2 ; i < prices.length ; i++){
            dp[i][0] = Math.max(dp[i-1][0],dp[i-2][1] - prices[i]);
            dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
        }
        return dp[prices.length-1][1];
    }
}

这种方法是把冷冻期没有作为一种状态表示，先假设没有冷冻期，那么就由买入、卖出两种状态，再结合冷冻期对买入的递推方程加以限制，今天的买入状态来源于昨天的买入状态或前天的卖出状态（相当于把冷冻期融合进这里了）

9.714.买卖股票的最佳时机含手续费

将手续费包含进递推公式即可

1.dp数组及下标含义

dp[i][j] : 第i天状态j下所持有的最大现金数量

0:持有

1:不持有

2.递推公式

dp[i][0] = Math.max(dp[i-1][0] , dp[i-1][1] - prices[i]);

dp[i][1] = Math.max(dp[i-1][1] , dp[i-1][0] +prices[i] - fee);

3.初始化

dp[0][0] = - prices[i];

dp[0][1] = 0;

4.遍历顺序

正序遍历

5.dp模拟

股票问题总结篇

参考：Leetcode股票问题总结篇

Renas_TJOvO

关注

39
点赞
踩
34

收藏

觉得还不错? 一键收藏
0
评论
代码随想录刷题记录-21 动态规划（5）习题

这道题是树形DP的入门题目，所谓树形DP就是在树上进行递归公式的推导。只不过平时我们习惯了在一维数组或者二维数组上推导公式，一下子换成了树，就需要对树的遍历方式足够了解。Leetcode股票问题总结篇。
复制链接

扫一扫