Candy 分配糖果

题目链接：https://leetcode.com/problems/candy/

1.题目描述

有N个孩子站成一排，每个孩子有一个分值。现在你需要为这些孩子分配糖果，但需要满足下面的需求。

• 每个孩子至少分一个。
• 拥有较高分值的孩子得到的糖果要比与他相邻的孩子得到的数量多。

那么最少需要给这些孩子分配多少糖果？
下面的方法的时间复杂度是O(n)，空间复杂度为O(1)。

2.思路分析

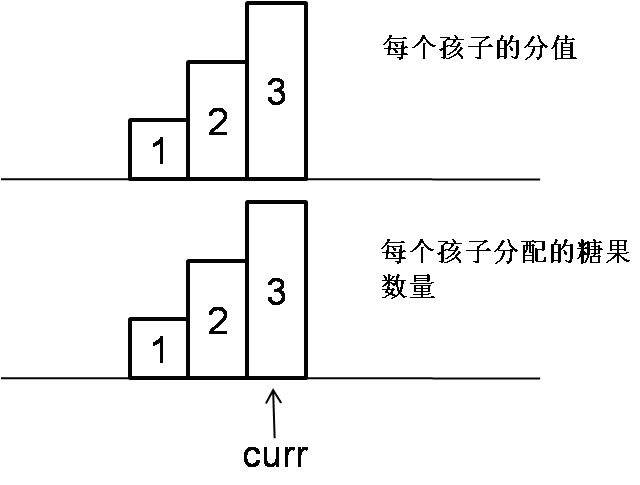
如果孩子当前的分值大于前一个孩子，当前孩子分得糖果数量应该是 前一个孩子分得糖果数加1。下图中cur代表当前孩子，图中上半部分对应每个孩子的分值，下半部分对应每个孩子分配的糖果数，后文中此类图形同理。

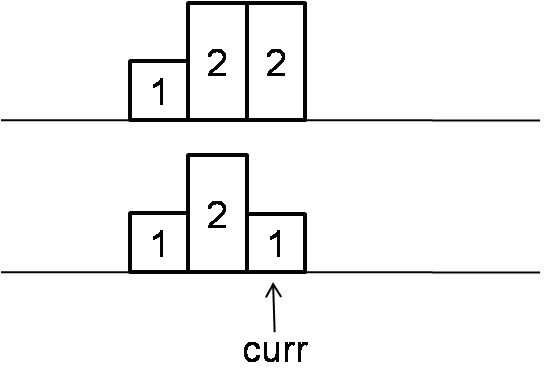
如果当前孩子的分值等于前一个孩子的分值，则当前孩子所分得糖果数量应该是1。（满足题意的前提下，分配最少糖果）

如果当前孩子的分值小于前一个孩子的，所分苹果数量需按以下几种情况分析。

孩子所具有的分值连续下降时，那么我们使用countDown来存放连续下降数。下图中，在curr位置处countDown = 2。(3-2，2-1)

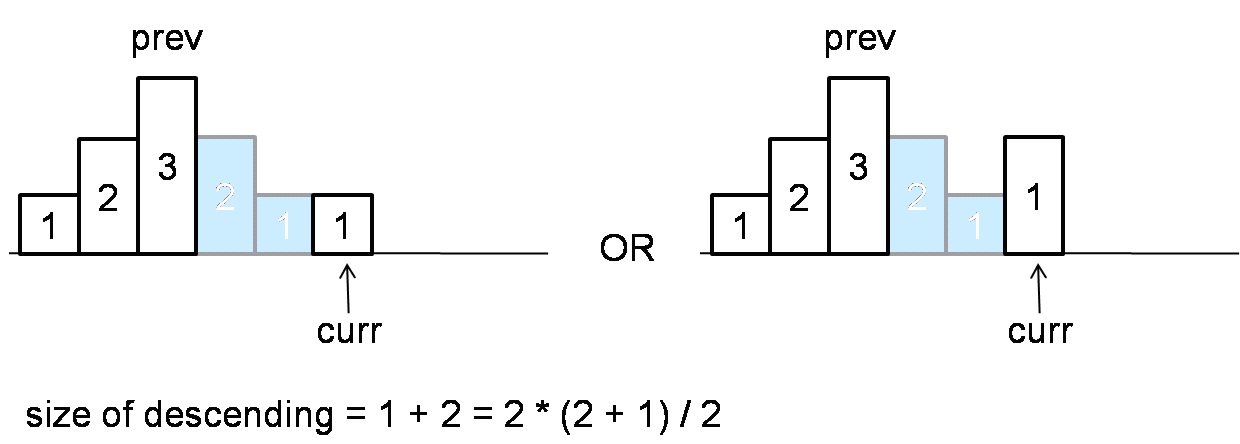
如果在下降序列中，当前值等于前一个人的值或大于前一个人的值，那么不在构成下降序列，那么我们将通过数列求和公式来计算这段连续下降序列的长度。下图为等差数列求和公式。

当计算下降区间长度时，需要考虑pre变量。下图中pre为2，因此接下来的两次糖果分配数量，无法按一次递减的方式分配，因为这样，因此第2次分配的数量将会是0，而每个孩子最少要分配一个。

在这种情况下，countDown >= prew，这样我们需要修改pre位置处为孩子分配的糖果数，pre = countdown – pre + 1。修正后可以保证每个孩子至少分配一个。

3.实现代码

public int candy(int[] ratings) {
    int pre = 1, countDown = 0, total = 1;
    for (int i = 1; i < ratings.length; i++) {
        if (ratings[i] >= ratings[i - 1]) {
            if (countDown > 0) {
                total += countDown * (countDown + 1) / 2;   
                if (countDown >= pre) { 
                    total += countDown - pre + 1;
                }
                pre = 1; 
                countDown = 0;
            }
            pre = ratings[i] == ratings[i - 1] ? 
                         1 : pre + 1;  prev + 1
            total += pre;
        }
        else {
            countDown++;
        }
    }
    if (countDown > 0) {    
        total += countDown * (countDown + 1) / 2;
        if (countDown >= pre) {
            total += countDown - pre + 1;
        }
    }
    return total;
}

原文地址：http://www.allenlipeng47.com/blog/index.php/2016/07/21/candy/