FFT详解&大数乘法

分享一个写的非常好的博客
http://blog.csdn.net/u013351484/article/details/48739415
http://blog.csdn.net/u013351484/article/details/48809943
比起一些写的看都看不懂的文章好到不知到哪去了

引入

传统的乘法的方法类似于利用列竖式的方法，时间复杂度为$O(N^{2})$。但是利用FFT的方法，我们可以把时间复杂度降到$O(NlogN)$。

系数表示法

设A和B是两个很大的数，C=A*B。把这两个数转换为类似幂级数的形式，即：（不足位数的补足前导0）
$A=a_{0}+a_{1}x+a_{2}x^{2}+……+a_{n-1}x^{n-1}$
$B=b_{0}+b_{1}x+b_{2}x^{2}+……+b_{n-1}x^{n-1}$
（接下来所说的都以A为例，B同理）
其中$a_{0}、a_{1}...a_{n-1}$分别表示A的第一位、第二位…第n位。这样我们就能用一个向量$(a_{0},a_{1},...,a_{n-1})$来表示A，这种表示方法叫做系数表示法，当x取10时就是我们常用的表示法。

点值表示法

我们发现这个幂级数的x其实是可以任取的，令：
$A(x)=a_{0}+a_{1}x+a_{2}x^{2}+……+a_{n-1}x^{n-1}$
对于这个n-1次的函数，最多只需n个点即可唯一确定这个函数，也就是说我们取这n个点：
$\{(0,A(0)),(1,A(1)),...,(n-1,A(n-1))\}$
即可唯一确定这个函数了，继而确定这个数A，换句话说A这个数唯一地对应了这n个点的集合，根据这n个点的集合也能反推出A。这种表示方法叫点值表示法。

点值表示法的计算方法

这样我们就找到了一种新的计算方式，令A、B分别由：
$\{(0,A(0)),(1,A(1)),...,(n-1,A(n-1))\}$
$\{(0,B(0)),(1,B(1)),...,(n-1,B(n-1))\}$
得到，将对应点的y坐标相乘：
$\{(0,A(0)*B(0)),(1,A(1)*B(1)),...,(n-1,A(n-1)*B(n-1))\}$
显然这就是C的点值表达式。考虑到两个n位数相乘的结果长度会加倍，所以一般都要取2n个点进行计算。

下面分析这个算法的时间复杂度：
1、得到两个数的点值表达式，因为每个点都要$O(N)$次计算，所以这一步的复杂度是$O(N^{2})$；
2、点值对应相乘，只需做$O(N)$次；
3、还原成系数表达式，一般来说只能采用高斯消元法，时间复杂度还是$O(N^{2})$。
所以我们是用更高级的方法得到了一样复杂度的做法吗？
其实不是的，这个算法是根本无法实现的。。。
先不说还要用高斯消元法，单单是得到n个点就无法实现：在整数集合内根本无法接受形如$x^{n-1}$的计算还不能取模。
但是，点值表达法却是FFT的关键一步。

离散傅里叶变换（DFT）

约定

所有有关DFT和FFT所需的约定都会放在这里，留心一下即可。
1、A和B是两个乘数，C是乘积。A和B的位数都必须是2的幂次，如果不是2的幂次就补足前导0，这是为了保证之后的二分能够正确进行。又因为C的位数要加倍，所以A和B的位数还需加倍，设这个位数为n。

复数的知识

复数的表示

在复平面上任何一个复数z都能表示成为一个向量，即：
$z=r(cos\theta +isin\theta)$
其中r是z的模长，$\theta$是向量与x轴的夹角，称之为幅角。
定义：$e^{i\theta} = cos\theta +isin\theta$
则有：$z=r*e^{i\theta}$
由此可以推出：$(cos\theta +isin\theta)^{\alpha}=(cos\alpha\theta +isin\alpha\theta)$
这就是棣莫弗公式。

单位根和本原根

在复数集下满足方程$x^{n}=1$的解一共有n个，这n个解构成1的n次单位根。并且这n个根中存在至少一个根$w_{n}$使得$w_{n}$的1~n次恰好就是这些n次单位根，称$w_{n}$为本原根。
换句话说：
$w_{n}^{0}、w_{n}^{1}、w_{n}^{2}、...、w_{n}^{n-1}$
这n个数互不相同，并且这n个数的n次方都是1。
如果我们把这n个复数在复平面上表示出来，我们发现这n个复数恰好平分360度。这个东西可以用棣莫弗公式来证明，因为复数的1次方、2次方、3次方···恰好就是幅角的1倍、2倍、3倍···
由此我们可以得到一个通用的本原根：（说通用是因为有些情况下本原根不止一个）
$w_{n} = cos\frac{2\pi}{n}+isin\frac{2\pi}{n}$

x的选取

之前提到x的选取是任意的，而DFT的神奇之处在于x取的就是n次单位根。然后我们能把A写成这样：
$A(x) = \sum_{j=0}^{n-1}a_{j}*x^{j}$
之前已经说了要取n个点，所以令：
$y_{k} = A(w_{n}^{k}) = \sum_{j=0}^{n-1}a_{j}w_{n}^{kj}$（latex不让打两次指数，相当于本原根的k次的j次）
其中$0<=k<=n-1$。
然后在回到之前的点值表示法，由于x坐标的选取都是固定的，所以我们直接用y坐标来表示这个数。因此我们完成了从：
$a=\{a_0,a_1,a_2,...,a_n-1\}$（系数表示法）到：
$y=\{y_0,y_1,y_2,...,y_n-1\}$（点值表示法）的转换。
称y为a的离散傅里叶变换(Discrete Fourier Transform,DFT)。

快速傅里叶变换（FFT）

遗憾的是，虽然DFT看起来更加高级，但依然改变不了它$O(N^{2})$的事实，事实上它连$O(N^{2})$都不如，因为大量的浮点数运算会带来更大的常数。
接下来的FFT就能在$O(NlogN)$的时间里完成从a到y的变换。

裂项

构造两个全新的次数界为n/2的多项式：
$A^{[0]}(x)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{n/2-1}$
$A^{[1]}(x)=a_1+a_3x+a_5x^2+...+a_{n-1}x^{n/2-1}$
显然有：
$A(k) = A^{[0]}(k^2)+k*A^{[1]}(k^2)$
这样，原问题：
$A(x)$在$w_{n}^{0}、w_{n}^{1}、w_{n}^{2}、...、w_{n}^{n-1}$
就转化为：
$A^{[0]}$和$A^{[1]}$在$(w_{n}^{0})^2、(w_{n}^{1})^2、(w_{n}^{2})^2、...、(w_{n}^{n-1})^2$
类似于归并排序，这样不断分裂下去直到结束。

递归

那么现在已经的两个多项式如何递归下去？因为转化之后的问题和原问题并不是完全符合的（多了一个平方）。
然而这个问题只需套用一下之前的棣莫弗公式，复数的平方可以看做幅角加倍，而幅角加倍的结果就是复数$w_n$变为了$w_{n/2}$。
一般地：
$w_{dn}^{dk} = w_{n}^{k}$ 称为相消定理。

所以：
$(w_{n}^{0})^2、(w_{n}^{1})^2、(w_{n}^{2})^2、...、(w_{n}^{n-1})^2$
就能转化为：
$w_{n/2}^{0}、w_{n/2}^{1}、w_{n/2}^{2}、...、w_{n/2}^{n-1}$
这样一来只要替换本原根，子问题就和原问题一模一样啦！

还原

现在我们已经得到了两个子问题的解，如何合并成原问题的解？
举一个n=4的例子：
$y_0=A(w_{4}^{0})=A^{[0]}((w_4^0)^2)+w_4^0A^{[1]}((w_4^0)^2)$
$y_1=A(w_{4}^{1})=A^{[0]}((w_4^1)^2)+w_4^1A^{[1]}((w_4^1)^2)$
$y_2=A(w_{4}^{2})=A^{[0]}((w_4^2)^2)+w_4^2A^{[1]}((w_4^2)^2)$
$y_3=A(w_{4}^{3})=A^{[0]}((w_4^3)^2)+w_4^3A^{[1]}((w_4^3)^2)$
根据相消定理可以得到：
$y_0=A(w_{4}^{0})=A^{[0]}(w_2^0)+w_4^0A^{[1]}(w_2^0)$
$y_1=A(w_{4}^{1})=A^{[0]}(w_2^1)+w_4^1A^{[1]}(w_2^1)$
$y_2=A(w_{4}^{2})=A^{[0]}(w_2^2)+w_4^2A^{[1]}(w_2^2)$
$y_3=A(w_{4}^{3})=A^{[0]}(w_2^3)+w_4^3A^{[1]}(w_2^3)$
套用一下两个公式：
1、$w_n^{k+n/2} = w_n^k*w_n^{n/2}=-w_n^k$
2、$w_n^{k+n} = w_n^k*w_n^{n}=w_n^k$
就可以得到：
$y_0=A(w_{4}^{0})=A^{[0]}(w_2^0)+w_4^0A^{[1]}(w_2^0)$
$y_1=A(w_{4}^{1})=A^{[0]}(w_2^1)+w_4^1A^{[1]}(w_2^1)$
$y_2=A(w_{4}^{2})=A^{[0]}(w_2^0)-w_4^0A^{[1]}(w_2^0)$
$y_3=A(w_{4}^{3})=A^{[0]}(w_2^1)-w_4^1A^{[1]}(w_2^1)$
由此我们可以在$O(NlogN)$的时间里完成从a到y的转换，这个过程就是快速傅里叶变换。

逆快速傅里叶变换

在经过FFT之后我们可以在$O(N)$的时间里求出C的点值表达式。但是问题来了，怎样从点值表达式回到系数表达式？

插值

构造一个范德蒙德矩阵$V$满足：
$\begin{bmatrix}y_0\\ y_1\\ y_2\\ :\\ y_n-1\end{bmatrix}$=$\begin{bmatrix}1 &1 &1 & ... &1 \\ 1& w_n & w_n^2 & ... & w_n^{n-1} \\ 1& w_n^2 & w_n^4 & ... & w_n^{2(n-1)}\\ :& : & : & : & :\\ 1 & w_n^{n-1} & w_n^{2(n-1)} & ... & w_n^{(n-1)(n-1)}\end{bmatrix}$$\begin{bmatrix}a_0\\ a_1\\ a_2\\ :\\ a_n-1\end{bmatrix}$
不妨记做$a=Vy$，而之前的FFT就可以看作是计算一次$V$。
从代数的角度来看，FFT的逆运算就是$V$的逆运算，而$V$的逆运算是什么？显然是$V^{-1}$，也就是逆矩阵！因为有：
$aV^{-1}=VV^{-1}y$，即：$y=aV^{-1}$
具体的证明就不证了，那个博客里有，扔结论：
对于第j行第k列，0<=j,k<=n-1，$V$中的值为$w_n^{kj}$，而$V^{-1}$z中的值为$\frac{w_n^{-kj}}{n}$。
所以有：
$a_{k} = \frac{1}{n} \sum_{j=0}^{n-1}a_{j}w_{n}^{-kj}$

逆快速傅里叶变换

之后，我们只要对C的y套用一遍FFT，根据棣莫弗公式，当指数取反时，对应的幅角也取反，实部的cos符号不变，虚部的sin取反，然后算完之后对整个a除以n即可。然后再四舍五入进进位啥的就做完啦！

大数乘法（递归版FFT）

#include<cmath>
#include<cstdio>
#include<vector>
#include<queue>
#include<cstring>
#include<iomanip>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#define ll long long
#define inf 1000000000
#define mod 1000000007
#define N 350000
#define fo(i,a,b) for(i=a;i<=b;i++)
#define fd(i,a,b) for(i=a;i>=b;i--)
using namespace std;
const double pi = 3.141592653;
char s1[N>>1],s2[N>>1];
double rea[N],ina[N],reb[N],inb[N],ret[N],intt[N];
int i,len1,len2,lent,lenres,len;
int res[N>>1];
void FFT(double *reA,double *inA,int n,int flag)
{
    if (n == 1) return;
    int k,u,i;
    double reWm = cos(2*pi/n) , inWm = sin(2*pi/n);//本原根
    if (flag) inWm = -inWm;
    double reW = 1.0 , inW = 0.0;
    for (k = 1,u = 0;k < n; k += 2,u++)//奇数项和偶数项分开
        {ret[u] = reA[k]; intt[u] = inA[k];}
    for (k = 2;k < n; k += 2)
        {reA[k/2] = reA[k]; inA[k/2] = inA[k];}
    for (k = u,i = 0;k < n && i < u; k++,i++)
        {reA[k] = ret[i]; inA[k] = intt[i];}
    FFT(reA,inA,n/2,flag); FFT(reA+n/2,inA+n/2,n/2,flag);
    fo(k,0,n/2-1)//合并
        {
            int tag = n / 2 + k;
            double reT = reW * reA[tag] - inW * inA[tag];
            double inT = reW * inA[tag] + inW * reA[tag];
            double reU = reA[k] , inU = inA[k];
            reA[k] = reU + reT; inA[k] = inU + inT;
            reA[tag] = reU - reT; inA[tag] = inU - inT;
            double reWt = reW * reWm - inW * inWm;
            double inWt = reW * inWm + inW * reWm;
            reW = reWt; inW = inWt;
        }
}
int main()
{
    while (~scanf("%s%s",s1,s2)) {
        memset(res, 0 , sizeof(res)); 
        memset(rea, 0 , sizeof(rea));  
        memset(ina, 0 , sizeof(ina));  
        memset(reb, 0 , sizeof(reb));  
        memset(inb, 0 , sizeof(inb));  
    len1 = strlen(s1); len2 = strlen(s2);
    lent = (len1 > len2 ? len1 : len2); len = 1;
    while (len < lent) len <<= 1; len <<= 1;
    fo(i,0,len-1)
        {
            if (i < len1) rea[i] = (double) s1[len1-i-1] - '0';
            if (i < len2) reb[i] = (double) s2[len2-i-1] - '0';
            ina[i] = inb[i] = 0.0;
        }
    FFT(rea,ina,len,0); FFT(reb,inb,len,0);//求出a、b的点值表示法 
    fo(i,0,len-1)//求出c的点值表示法 
        {
            //printf("%.5lf %.5lf\n",rea[i],ina[i]);
            double rec = rea[i] * reb[i] - ina[i] * inb[i];
            double inc = rea[i] * inb[i] + ina[i] * reb[i];
            rea[i] = rec; ina[i] = inc;
        }
    FFT(rea,ina,len,1);//求出c的系数表示法
    fo(i,0,len-1) {rea[i] /= len; ina[i] /= len;}

    fo(i,0,len-1) res[i] = (int)(rea[i] + 0.5);
    fo(i,0,len-1) res[i+1] += res[i] / 10 , res[i] %= 10;

    lenres = len1 + len2 + 2;
    while (res[lenres] == 0 && lenres > 0) lenres--;
    fd(i,lenres,0) printf("%d",res[i]); printf("\n");}
    return 0;
}

大数乘法（迭代版FFT）

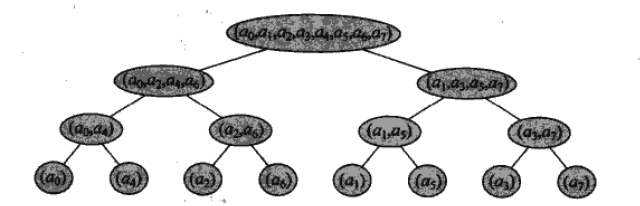
把递归的过程写成迭代版本就能省下不断递归和不断列项所产生的常数（想想一个$NlogN$的算法只能跑几十万甚至几万就知道浮点数常数有多大了）

贴一张图：

也是类似于归并排序，只不过这个过程使用循环而并非递归完成的。
这样做有什么好处？
1、省常数。整个序列从一开始就可以完成重排，而并非递归每次都需排序。
2、代码好写。由于省掉了重排，所以代码只要写合并就行了。
3、递归改成非递归总是好一些。

PS这个合并操作被称为蝴蝶操作，但我并不明白为啥这还要特地搞个名字。。。
然后至于这个重拍操作，神奇的来了！只要把二进制表达反转一下就是结果了！举个例子，$(3)_{10}=(011)_2，6_{10}=(110)_2$，所以从左数第四个应该是$a_6$。十分优美的结论。

#include<cmath>
#include<cstdio>
#include<vector>
#include<queue>
#include<cstring>
#include<iomanip>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#define ll long long
#define inf 1000000000
#define mod 1000000007
#define N 350000
#define fo(i,a,b) for(i=a;i<=b;i++)
#define fd(i,a,b) for(i=a;i>=b;i--)
using namespace std;
const double pi = 3.141592653;
char s1[N>>1],s2[N>>1];
double rea[N],ina[N],reb[N],inb[N],ret[N],intt[N];
int i,len1,len2,lent,lenres,len;
int res[N>>1];
void Swap(double &x,double &y)
{double t = x; x = y; y = t;}
int rev(int x,int len)
{
    int ans = 0,i;
    fo(i,1,len) {ans<<=1; ans|=x&1; x>>=1;}
    return ans;
}
void FFT(double *reA,double *inA,int n,int flag)
{
    int s,i,j,k; int lgn = log((double)n) / log((double)2);
    fo(i,0,n-1)//数组重排
        {
            j = rev(i,lgn);
            if (j > i) {Swap(reA[i],reA[j]); Swap(inA[i],inA[j]);}
        }

    fo(s,1,lgn)
        {
            int m = (1 << s);
            double reWm = cos(2*pi/m) , inWm = sin(2*pi/m);
            if (flag) inWm = -inWm;
            for (k = 0;k < n; k += m)
                {
                    double reW = 1.0 , inW = 0.0;
                    fo(j,0,m/2-1)
                        {
                            int tag = k + j + m / 2;
                            double reT = reW * reA[tag] - inW * inA[tag];
                            double inT = reW * inA[tag] + inW * reA[tag];
                            double reU = reA[k+j] , inU = inA[k+j];
                            reA[k+j] = reU + reT; inA[k+j] = inU + inT;
                            reA[tag] = reU - reT; inA[tag] = inU - inT;
                            double reWt = reW * reWm - inW * inWm;
                            double inWt = reW * inWm + inW * reWm;
                            reW = reWt; inW = inWt;
                        }
                }

        }

}
int main()
{
    while (~scanf("%s%s",s1,s2)) {
        memset(res, 0 , sizeof(res)); 
        memset(rea, 0 , sizeof(rea));  
        memset(ina, 0 , sizeof(ina));  
        memset(reb, 0 , sizeof(reb));  
        memset(inb, 0 , sizeof(inb));  
    len1 = strlen(s1); len2 = strlen(s2);
    lent = (len1 > len2 ? len1 : len2); len = 1;
    while (len < lent) len <<= 1; len <<= 1;
    fo(i,0,len-1)
        {
            if (i < len1) rea[i] = (double) s1[len1-i-1] - '0';
            if (i < len2) reb[i] = (double) s2[len2-i-1] - '0';
            ina[i] = inb[i] = 0.0;
        }
    FFT(rea,ina,len,0); FFT(reb,inb,len,0);//求出a、b的点值表示法 
    fo(i,0,len-1)//求出c的点值表示法 
        {
            //printf("%.5lf %.5lf\n",rea[i],ina[i]);
            double rec = rea[i] * reb[i] - ina[i] * inb[i];
            double inc = rea[i] * inb[i] + ina[i] * reb[i];
            rea[i] = rec; ina[i] = inc;
        }
    FFT(rea,ina,len,1);
    fo(i,0,len-1) {rea[i] /= len; ina[i] /= len;}

    fo(i,0,len-1) res[i] = (int)(rea[i] + 0.5);
    fo(i,0,len-1) res[i+1] += res[i] / 10 , res[i] %= 10;

    lenres = len1 + len2 + 2;
    while (res[lenres] == 0 && lenres > 0) lenres--;
    fd(i,lenres,0) printf("%d",res[i]); printf("\n");}
    return 0;
}