一、交叉熵损失函数(CE Loss,BCE Loss)
最开始理解交叉熵损失函数被自己搞的晕头转向的,最后发现是对随机变量的理解有偏差,不知道有没有读者和我有着一样的困惑,所以在本文开始之前,先介绍一下随机变量是啥。
什么是概率分布?
概率分布,是指用于表述随机变量取值的概率规律。随机变量的概率表示了一次试验中某一个结果发生的可能性大小 ,想象画在图上就是横坐标(自变量)是随机变量。根据随机变量所属类型的不同,概率分布取不同的表现形式。举个最简单的例子:抛一枚硬币,随机变量为抛硬币的结果,产生的结果的概率分布为:p(正面)=0.5,p(背面)=0.5
随机变量是什么?
随机变量是将随机试验的结果数量化,具有随机性的,注意是结果!!!在概率论中,概率质量函数(probability mass function,简写为pmf)是离散随机变量在各特定取值上的概率。一个概率质量函数的图像。函数的所有值必须非负,且总和为1。
如在抛50次硬币这个事件中,随机变量是指抛硬币获得正面的次数。不要把随机变量理解为试验的次数的取值!!!再拿二分类任务举个例子,二分类的随机变量就是看做0和1两个类别。二分类猫狗任务就相当于二项分布中的伯努利分布(试验次数为1时就叫伯努利分布,就相当于只丢一次硬币),因为去识别一张图片,最后试验的结果只能要么是猫要么是狗,这任务中的随机变量不是每一个训练样本(训练集中的每一张图片),而是分类的结果即猫or狗!在训练过程中,如果用交叉熵损失函数,假如p(x)是目标真实的分布,而q(x)是预测得来的分布。网络对每一个训练样本来讲,这张图片经过网络输出后得到的q(x)尽可能和这张图像的p(x)分布相等,x为类别的随机变量,x1为猫,x2为狗。如p(x1)=1,就是表示这张图片得到的x1这个类别的结果概率是1,所以由标签可知它的真实分布即p就是p(猫,狗)~(1,0),从训练来讲就是让这张训练样本图片经过网络输出后,得到的q(x)去无限接近上面p(猫,狗)-(1,0)这个分布。 拟合分布就是让预测分布的参数不断接近分布的参数!如p就是伯努利分布中的参数。所谓的交叉熵的交叉就是指这两个分布之间的交叉,让两个分布越接近则交叉熵损失越小。
要充分理解交叉熵损失函数,首先要理解相对熵,又称互熵。设p(x)和q(x)是两个概率分布,相对熵用来表示两个概率分布的差异,当两个随机分布相同时,它们的相对熵为零,当两个随机分布的差别增大时,它们的相对熵也会增大。
而相对熵=交叉熵-信息熵!!!
由于在机器学习和深度学习中,样本和标签已知(即p已知,样本就是xi),那么信息熵H(p)相当于常量,此时,只需拟合交叉熵,使交叉熵拟合为0即可。关键点:所以最小化交叉熵损失函数就相当于使得交叉熵公式里的p和q这两个概率分布(指交叉熵公式里的那两个乘法因子)的差异最小!式子中的n就是随机变量的取值集合,在这里就是类别数,p(xi)就是事件X=xi的概率。

信息熵(公式里的两个乘法因子都是指同一个分布的):
信息熵则是在结果出来之前对可能产生的信息量的期望,信息量表示一条信息消除不确定性的程度,如中国目前的高铁技术世界第一,这个概率为1,这句话本身是确定的,没有消除任何不确定性。而中国的高铁技术将一直保持世界第一,这句话是个不确定事件,包含的信息量就比较大。信息量的大小和事件发生的概率成反比。信息熵越小就表示这个事件发生的概率越大,-logP就是信息量的公式(P表示事件发生的概率)。
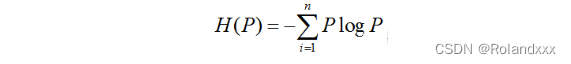
交叉熵(公式是针对一个样本的,公式里的两个乘法因子分别指两个分布,n为类别数):
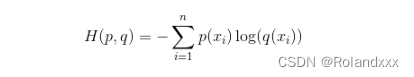
下面进入正题,也就是BCE Loss和CE Loss:
对于二分类交叉熵,下图的x1和x2是指两个类别,比如x1和x2分别代表猫和狗两类,p就是这个样本为猫的标签,这个标签可能是0也有可能是1;q就是这个样本被预测为猫的概率!

下图给出了多分类问题(实现为F.cross_entropy)和二分类问题(实现为F.binary_cross_entropy)的交叉熵损失公式,下图中多分类问题中的公式是针对单个样本的,公式里的i表示每一个类别。而对于二分类问题的公式即BCE loss,公式里的i表示每一个样本,所以要注意区分! 对于多分类问题即CE loss,假设真实标签的one-hot编码是:[0,0,…,1,…,0],预测的softmax概率为[0.1,0.3,…,0.4,…,0.1],那么Loss=-log(0.4)。对于二分类问题即BCE loss来说,每个样本就输出一个数字。

需要注意的是,BCE loss在pytorch中实现多分类损失时,也就是通过多个二分类来实现多分类时,target要转换成one-hot形式(只能有1个元素为1,其余都为0)。如下图所示,下图就是一个用BCE loss实现6分类的例子,BCE loss就把这个问题当成6个二分类实现,因为一个目标只能是属于一个类别,所以可以转换成one-hot形式。然后对于用BCE loss处理多分类问题的情况,最后其实返回的是每个类别的二分类损失求和的平均值,所以真正返回的是:4.7938/6 = 0.7990

二、Focal loss
Focal loss的本质:
- 首先给出原始二分类交叉熵的公式:
- 在二分类交叉熵损失的基础上,控制了正负样本的权重来解决了正负样本的不平衡,下图就是基于二分类交叉熵损失通过α来控制正负样本比例的例子,当α=0.5时,正负样本的比重是一样的。
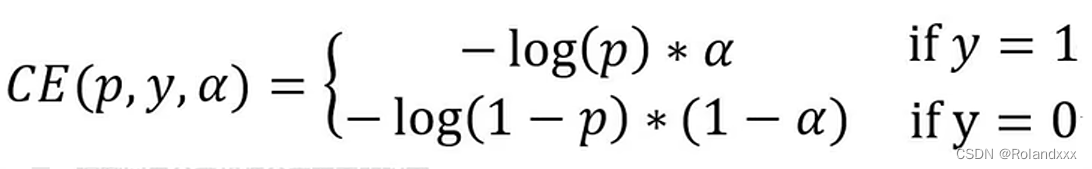
- 在上面图中损失的基础上,增加控制“容易分类和难分类样本的权重”来解决难例挖掘的问题。
- 结合这两个方法,就是最终的二分类的Focal loss(如下图所示),最前面红框的第一项是最普通的交叉熵;第二项是控制正负样本平衡的α参数;第三项是控制难易分类样本的平衡,即对于正样本而言,预测分数越接近于1的表示这个样本越简单,那么这个样本应该对损失的影响越小:
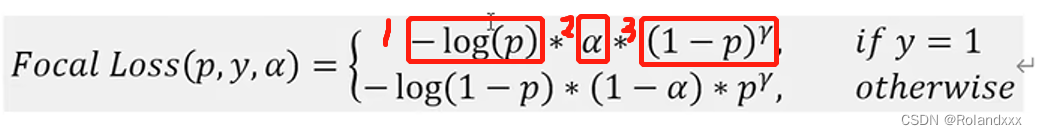
- 同理,多分类的Focal loss(softmax)的公式如下图所示:
Focal loss的具体代码实现:
# 参考了:
# 1. https://github.com/clcarwin/focal_loss_pytorch/blob/master/focalloss.py
# 2. https://github.com/c0nn3r/RetinaNet/blob/master/focal_loss.py
import torch
import torch.nn.functional as F
def focal_loss(logits, labels, gamma=2, reduction="mean"):
r"""
focal loss for multi classification(简洁版实现)
`https://arxiv.org/pdf/1708.02002.pdf`
FL(p_t)=-alpha(1-p_t)^{gamma}ln(p_t)
"""
# 这段代码比较简洁,具体可以看作者是怎么定义的,或者看 focal_lossv1 版本的实现
# 经测试,reduction 加不加结果都一样,但是为了保险,还是加上
# logits是过激活函数前的值,reduction="none"就是不对loss进行求mean或者sum 保留每个样本的CE loss
ce_loss = F.cross_entropy(logits, labels, reduction="none")
log_pt = -ce_loss
pt = torch.exp(log_pt)
weights = (1 - pt) ** gamma
fl = weights * ce_loss
if reduction == "sum":
fl = fl.sum()
elif reduction == "mean":
fl = fl.mean()
else:
raise ValueError(f"reduction '{reduction}' is not valid")
return fl
def balanced_focal_loss(logits, labels, alpha=0.25, gamma=2, reduction="mean"):
r"""
带平衡因子的 focal loss,这里的 alpha 在多分类中应该是个向量,向量中的每个值代表类别的权重。
但是为了简单起见,我们假设每个类一样,直接传 0.25。
如果是长尾数据集,则应该自行构造 alpha 向量,同时改写 focal loss 函数。
"""
return alpha * focal_loss(logits, labels, gamma, reduction)
def focal_lossv1(logits, labels, gamma=2):
r"""
focal loss for multi classification(第一版)
FL(p_t)=-alpha(1-p_t)^{gamma}ln(p_t)
"""
# pt = F.softmax(logits, dim=-1) # 直接调用可能会溢出
#什么是softmax的溢出:https://blog.csdn.net/qq_35054151/article/details/125891745
# 一个不会溢出的 trick
log_pt = F.log_softmax(logits, dim=-1) # 这里相当于 CE loss
#pt:tensor([[0.1617, 0.2182, 0.2946, 0.3255],
# [0.2455, 0.2010, 0.3314, 0.2221]])
pt = torch.exp(log_pt) # 通过 softmax 函数后打的分
labels = labels.view(-1, 1) # 多加一个维度,为使用 gather 函数做准备
#.gather第一个参数表示根据哪个维度,第二个参数表示按照索引列表index从input中选取指定元素
pt = pt.gather(1, labels) # 从pt中挑选出真实值对应的 softmax 打分,也可以使用独热编码实现
#pt,因为只有两个样本所以只有两项损失: tensor([[0.2182],
# [0.2221]])
ce_loss = -torch.log(pt)
weights = (1 - pt) ** gamma
#对应元素相乘
fl = weights * ce_loss
#大家都是默认取均值而不是取sum
fl = fl.mean()
return fl
if __name__ == "__main__":
#2个样本,4分类问题
logits = torch.tensor([[0.3, 0.6, 0.9, 1], [0.6, 0.4, 0.9, 0.5]])
labels = torch.tensor([1, 3])
print(focal_loss(logits, labels))
print(focal_loss(logits, labels, reduction="sum"))
print(focal_lossv1(logits, labels))
print(balanced_focal_loss(logits, labels))
Refer:
交叉熵损失原理详解
随机变量的理解
GAN交叉熵
从二分类(二项分布)到多分类(多项分布)
FocalLoss 对样本不平衡的权重调节和减低损失值
再记录几个好的文章非常实用:
一文搞懂F.cross_entropy的具体实现
一文搞懂F.binary_cross_entropy以及weight参数
softmax loss详解,softmax与交叉熵的关系
二分类问题,应该选择sigmoid还是softmax?






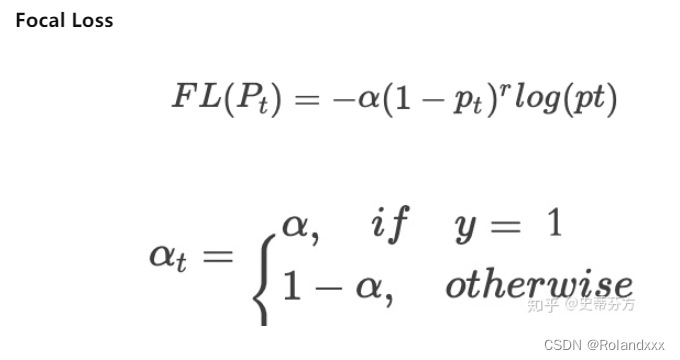


















 4199
4199

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








