高斯分布与马氏距离

本文转自：https://blog.csdn.net/qq_28038207/article/details/81006453 

• 给定随机变量xi(i=1,...,N)xi(i=1,...,N)构成的矢量XX，它的均值是X¯=E(X)X¯=E(X)，而ΔX=X−X¯ΔX=X−X¯，其协方差矩阵

  Σ=E(ΔXΔXT)Σ=E(ΔXΔXT)

  
  可知，矩阵ΣΣ的对角元是单个变量xixi的方差，而非对角元是交叉协方差。

   

• 如果XX的概率密度分布形如

  P(X¯+ΔX)=(2π)−N/2det(Σ−1)1/2exp(−ΔXTΣ−1ΔX/2)P(X¯+ΔX)=(2π)−N/2det(Σ−1)1/2exp(−ΔXTΣ−1ΔX/2)

  
  其中Σ−1Σ−1是半正定矩阵，那么，变量xixi遵循一个联合高斯分布。均值和协方差是X¯和ΣX¯和Σ。

   

• 特殊情况：Σ=σ2IΣ=σ2I，为各向同性高斯分布 

  P(X)=(2π−−√σ)−Nexp(−∑(xi−x¯i)2/2σ2)P(X)=(2πσ)−Nexp(−∑(xi−x¯i)2/2σ2)

   

• 马氏距离 

  ||X−Y||=((X−Y)TΣ−1(X−Y))1/2||X−Y||=((X−Y)TΣ−1(X−Y))1/2

  
  可以看出，高斯概率密度函数是变量马氏距离的函数。

   

• 理解马氏距离

  一个地区的人用两个数据表示(身高/cm，体重/g)。了解到这个地区的数据均值是(170，60000)。越接近这个体型的人数越多 
  一个人a数据是(180，600100)，另一个人b的数据是(175，63000)。如果采用欧式距离的话，a更接近。因此推出有a身材的人更多。 
  但实际上，我们看来应该是b更接近平均身材。所以，欧式距离有问题。 
  解决方法引入数据方差，计算(x−x¯)/σ(x−x¯)/σ的欧式距离

到目前，大家可以理解协协方差矩阵是对角阵的马氏距离：距离均值越近，概率越大。而距离与方差有关。那么马氏距离中的协方差怎么回事？ 
协方差矩阵ΣΣ一般是对称正定矩阵，可以写成Σ=UTDUΣ=UTDU，D=(σ21,...,σ2N)D=(σ12,...,σN2)是对角矩阵，U是正交矩阵。记X′=UXX′=UX和X′¯=UX¯X′¯=UX¯，则 

exp(−(X−X¯)TΣ−1(X−X¯)/2)=exp(−(X′−X¯′)TUΣ−1UT(X′−X¯′)/2)=exp(−(X′−X¯′)TD−1(X′−X¯′)/2)exp(−(X−X¯)TΣ−1(X−X¯)/2)=exp(−(X′−X¯′)TUΣ−1UT(X′−X¯′)/2)=exp(−(X′−X¯′)TD−1(X′−X¯′)/2)

这样就可以理解了：马氏距离在另一个坐标系下是独立变量的距离。距离越远，概率越小。距离是∑(Δxi/σi)2∑(Δxi/σi)2。 
记住，左乘正交矩阵相当于坐标轴进行了刚体欧式运动。欧式运动后，如下图，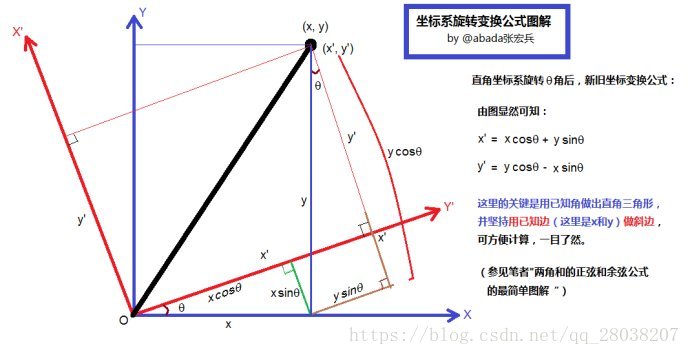 

 

上面操作的效果如下：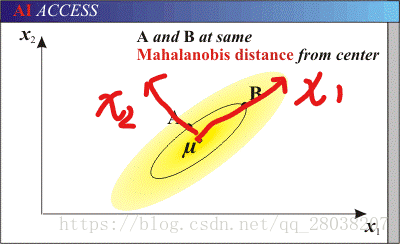 
 
这样，不同变量独立了。协方差矩阵是对角矩阵。也可以进一步缩放，变为各向同性的高斯分布。 
总结一下：马氏距离在另一个坐标系下协方差矩阵是对角阵的马氏距离。

• 为什么非要协方差？我就要方差不行吗？ 
  考虑x1=x2x1=x2，数据冗余的情况。如果只要方差那么x1x1投了2次票。通过马氏距离，D有一个元素是0。相当于少了一票。卧槽，起到了PCA的作用。

• 卡方分布：χ2nχn2分布是n个独立高斯随机变量的平方和的分布。当应用于有非奇异协方差矩阵ΣΣ的高斯随机变量vv时，(v−v¯)TΣ−1(v−v¯)(v−v¯)TΣ−1(v−v¯)的值满足χ2nχn2分布。

• 如果协方差矩阵是ΣΣ的高斯随机变量vv，那么，(v−v¯)TΣ+(v−v¯)(v−v¯)TΣ+(v−v¯)的值满足χ2rχr2分布，其中r=rank(Σ)r=rank(Σ)。