文章目录
计算理论导引 第7章 复杂性理论 III 的相关笔记,包括:完全NP类问题……
这部分最重要的内容是,如何证明一个 N P NP NP 问题是 N P C NPC NPC 问题,需要学习如何从 3 S A T 3SAT 3SAT 归约到这个问题。
第7章笔记 (III)
7.4 NP完全性
多项式时间可归约性
多项式时间可归约
Def 7.23:若存在多项式时间图灵机 M M M ,使得对于任何输入, M M M 停机时 f ( w ) f(w) f(w) 恰好在带子上,则称函数 f : Σ ∗ → Σ ∗ f:{\,}{\Sigma}^{\ast}\to{\Sigma}^{\ast} f:Σ∗→Σ∗ 为 多项式时间可计算函数
Def 7.24:称语言 A A A 多项式时间可归约到 B B B ,记为 A ≤ P B A{\leq}_PB A≤PB ,当存在多项式时间可计算函数 f : Σ ∗ → Σ ∗ f:{\,}{\Sigma}^{\ast}\to{\Sigma}^{\ast} f:Σ∗→Σ∗ ,使得对于每一个 w w w ,有: w ∈ A ⟺ f ( w ) ∈ B w{\in}A{\iff}f(w){\in}B w∈A⟺f(w)∈B
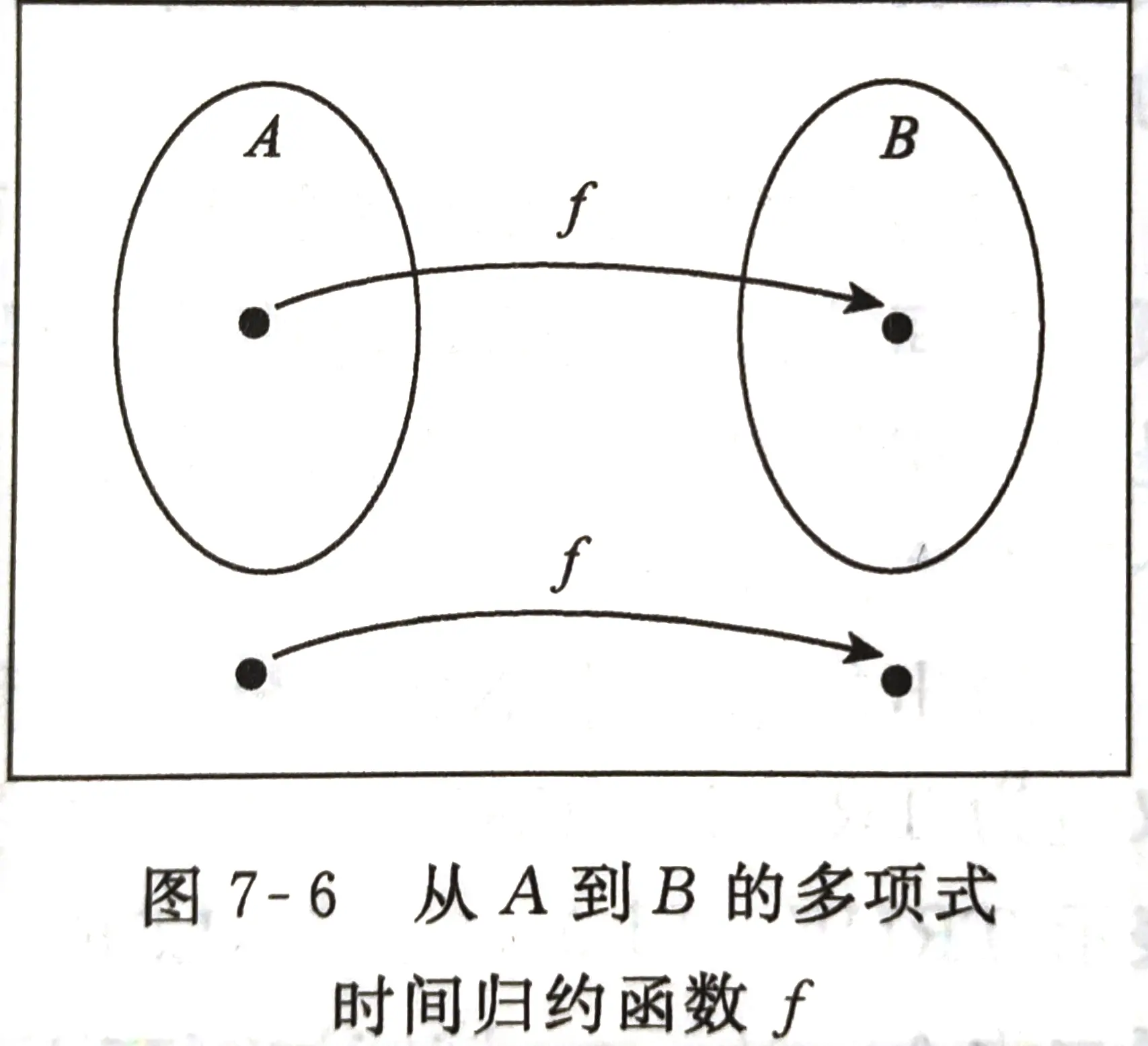
注意:归约相当于时把 A A A 的成员资格判定转化为 B B B 的成员资格判定,注意方向
Th 7.25:若 A ≤ P B A{\leq}_PB A≤PB 且 B ∈ P B{\in}P B∈P ,则 A ∈ P A\in P A∈P
证明:设 M M M 为 B B B 的多项式时间判定机,则构造 A A A 的多项式时间判定机 N N N ,对于输入 w w w :
- 先模拟多项式时间可计算函数,将 w w w 转化为 f ( w ) f(w) f(w)
- 再模拟 M M M ,判断 f ( w ) f(w) f(w) 是否属于 B B B
因为两个步骤的时间都是多项式时间,因而 N N N 也是多项式时间可判定,即 A ∈ P A\in P A∈P
可满足性问题
Def: S A T = { < ϕ > ∣ ϕ SAT=\{ {\lt}{\phi}{\gt}{\,}|{\,}{\phi} SAT={<ϕ>∣ϕ 是可满足的布尔公式 } \} }
解释:布尔表达式可满足性是指是否存在一个赋值或者指派方式使得表达式最终为真
例:文物鉴定,三件文物 A A A、 B B B、 C C C ,三位鉴定专家张、王、赵,每人的准确度 > 0.5 \gt 0.5 >0.5 (意思是每人鉴定的两个文物中至少有一个鉴定结果是准确的);现在让专家鉴定其中两个文物,正品为真,赝品为假:
| A | B | C | |
| 张 | 1 | 1 | |
| 王 | 1 | 1 | |
| 赵 | 0 | 1 |
问题:买那些文物好?由专家准确度得, A ∣ B A|B A∣B 、 B ∣ C B|C B∣C、 C ∣ ! B C|!B C∣!B 均为一,现在就需要知道对 A A A、 B B B、 C C C 的一组合理指派,使得: ( A ∣ B ) & ( B ∣ C ) & ( C ∣ ! B ) = 1 (A|B)\&(B|C)\&(C|!B)=1 (A∣B)&(B∣C)&(C∣!B)=1
Def 3nf:每个 子句 含有3个 文字 的合取范式(cnf),称为 3nf公式
例: ϕ = ( x 1 ∨ x 2 ‾ ∨ x 3 ‾ ) ∧ ( x 3 ∨ x 5 ‾ ∨ x 6 ) ∧ ( x 3 ∨ x 6 ‾ ∨ x 4 ) {\phi}=(x_1\vee\overline{x_2}\vee\overline{x_3})\wedge(x_3\vee\overline{x_5}\vee x_6)\wedge(x_3\vee\overline{x_6}\vee x_4) ϕ=(x1∨x2∨x3)∧(x3∨x5∨x6)∧(x3∨x6∨x4) 就是一个 3 n f 3nf 3nf
Th:k-合取范式可归约为满足性等价的的3-合取范式
证明:对于某一子句,其长度为 k k k :
- 当 k = 1 k=1 k=1 ,例如 x 1 x_1 x1 ,则可变为 x 1 ∨ x 1 ∨ x 1 x_1\vee x_1\vee x_1 x1∨x1∨x1 ,显然等价
- 当 k = 2 k=2 k=2 ,例如 x 1 ∨ x 2 x_1\vee x_2 x1∨x2 ,则可变为 x 1 ∨ x 2 ∨ x 2 x_1\vee x_2\vee x_2 x1∨x2∨x2 ,显然等价
- 当 k > 3 k>3 k>3 时,例如 x 1 ∨ x 2 ∨ x 3 ∨ x 4 ∨ x 5 x_1\vee x_2\vee x_3\vee x_4\vee x_5 x1∨x2∨x3∨x4∨x5 ,可拆为 ( x 1 ∨ x 2 ∨ y 1 ) ∧ ( ¬ y 1 ∨ x 3 ∨ y 2 ) ∧ ( ¬ y 2 ∨ x 4 ∨ x 5 ) (x_1\vee x_2\vee y_1){\wedge}(\neg y_1\vee x_3\vee y_2)\wedge(\neg y_2\vee x_4\vee x_5) (x1∨x2∨y1)∧(¬y1∨x3∨y2)∧(¬y2∨x4∨x5) ;当原式为1时, x i x_i xi 中至少有一个数为1;不失一般性,设 x 1 = 1 x_1=1 x1=1 ,则可令 y 1 = y 2 = 1 y_1=y_2=1 y1=y2=1 ,则原式仍然为1
Def: 3 S A T = { < ϕ > ∣ ϕ 3SAT=\{ {\lt}{\phi}{\gt}{\,}|{\,}{\phi} 3SAT={<ϕ>∣ϕ 是可满足的 3 n f 3nf 3nf 公式 } \} }
NP完全问题
NP完全性定义
Def 7.27:称语言 B B B 为 NP完全的(NPC),当且仅当其同时满足下面两个条件:
- B ∈ N P B{\in}NP B∈NP
- ∀ A ∈ N P {\forall}A{\in}NP ∀A∈NP , A A A 都多项式时间可归约到 B B B
Th 7.28:若语言 B B B 是完全的,且 B ∈ P B\in P B∈P ,则 P = N P P=NP P=NP
(显然,若 N P NP NP 完全问题是 P P P 类问题,那么所有 N P NP NP 问题都可以归约到 N P NP NP 完全问题,进而得到多项式时间的算法)
Th: N P C NPC NPC 问题的四个性质:(第四条最重要)
- 若 A , B ∈ N P C A,B{\in}NPC A,B∈NPC ,则 A ≤ p B A{\leq}_pB A≤pB (可相互归约)
- A ∈ N P C A{\in}NPC A∈NPC ,若 A ∈ P A{\in}P A∈P ,则 N P = P NP=P NP=P
- A ∈ N P C A{\in}NPC A∈NPC ,若 A ∉ P A{\notin}P A∈/P ,则 N P ∩ P = ∅ NP{\cap}P=\varnothing NP∩P=∅
- A ∈ N P C A{\in}NPC A∈NPC, B ∈ N P B{\in}NP B∈NP ,若 A ≤ p B A{\leq}_pB A≤pB ,则 B ∈ N P C B{\in}NPC B∈NPC
库克-列文定理
Th 7.30: S A T SAT SAT 是 N P NP NP 完全的
Th 7.22: S A T ∈ P SAT{\in}P SAT∈P ,当且仅当 P = N P P=NP P=NP
证明:证明 S A T SAT SAT 是 N P NP NP 完全的分两步:首先要证明 S A T ∈ N P SAT{\in}NP SAT∈NP ,然后要证明任意 N P NP NP 问题可归约到 S A T SAT SAT 上
① 证明 S A T ∈ N P SAT{\in}NP SAT∈NP
显然,构造一个非确定图灵机 M M M ,对某一输入的布尔表达式 ϕ \phi ϕ 中的变量 x i x_i xi 随机非确定指派为0或1;当所有路径中只要出现一条满足 ϕ = 1 \phi=1 ϕ=1 ,即可知该布尔表达式可满足;即 M M M 为该语言的非确定型多项式时间判别机,故 S A T ∈ N P SAT{\in}NP SAT∈NP
② 证明任意 N P NP NP 问题可归约到 S A T SAT SAT
对于某个 N P NP NP 问题的判别机 N N N,设其判定步数为 n k n^k nk,将所有的瞬时描述前后加上井号,构成如下的表:
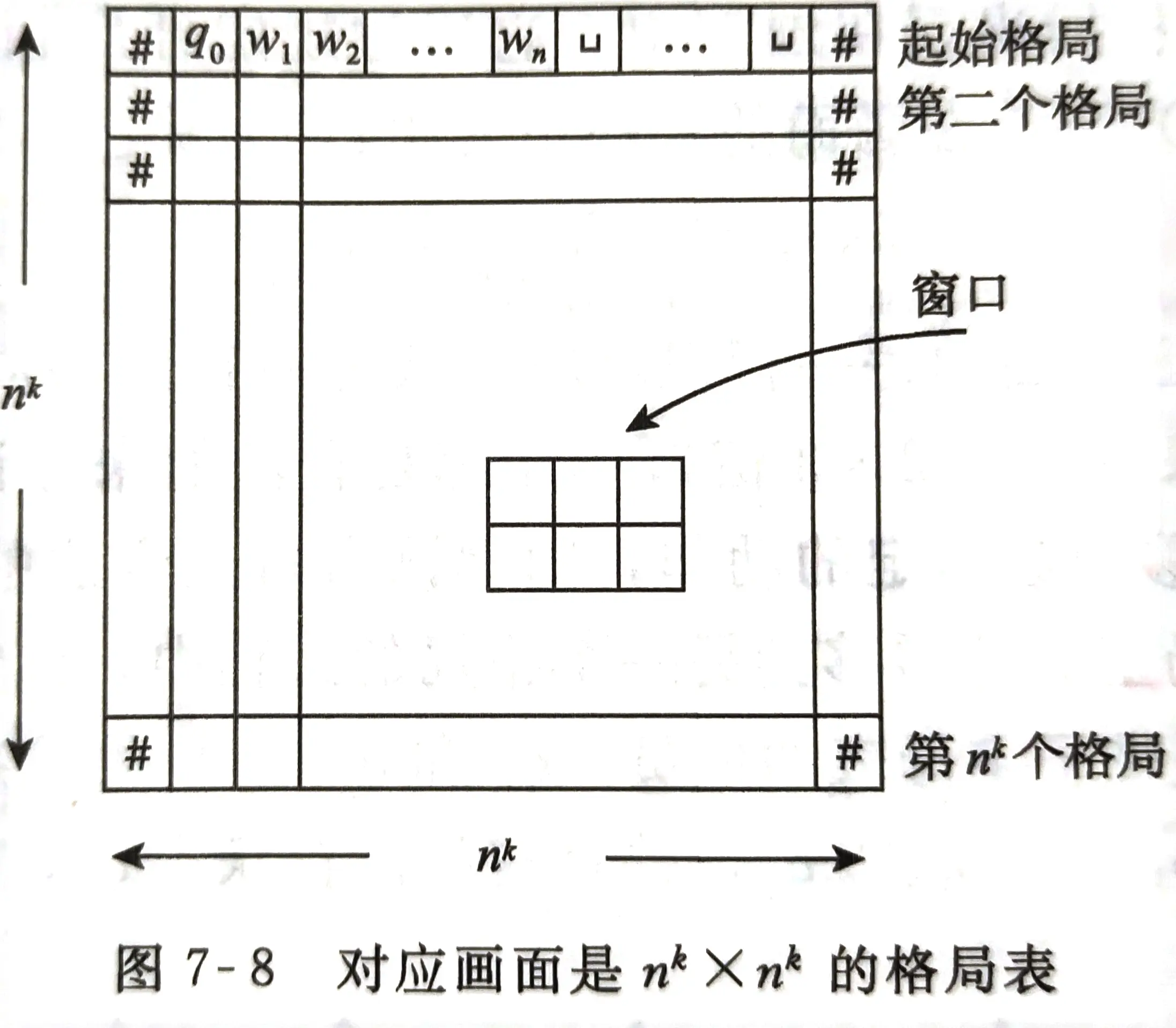
(表、行、单元格、2*3的子表分别称为画面、格局、单元、窗口)
设计:现在根据这个表格设计
ϕ
\phi
ϕ ,使其变量的一个满足赋值确实对应
N
N
N 在
w
w
w 上的一个接受画面:令
C
=
Q
∪
Γ
∪
{
♯
}
C=Q{\cup}\Gamma\cup \{\sharp\}
C=Q∪Γ∪{♯} (
Q
Q
Q 为状态集,
Γ
\Gamma
Γ 为带字母集),则设计
ϕ
\phi
ϕ 的变量
x
i
,
j
,
s
x_{i,j,s}
xi,j,s,意为表格中的第
[
i
,
j
]
[i,j]
[i,j] 位置为
C
C
C 中第
s
s
s 个字母;则:
ϕ
=
ϕ
c
e
l
l
∧
ϕ
s
t
a
r
t
∧
ϕ
m
o
v
e
∧
ϕ
a
c
c
e
p
t
\phi=\phi_{cell} \wedge \phi_{start} \wedge \phi_{move} \wedge \phi_{accept}
ϕ=ϕcell∧ϕstart∧ϕmove∧ϕaccept
(1)
ϕ
c
e
l
l
{\phi}_{cell}
ϕcell :保证表格的基本结构,即每个单元有且仅有一个字母
(2) ϕ s t a r t {\phi}_{start} ϕstart :保证表格第一行必须是 w w w
(3) ϕ a c c e p t {\phi}_{accept} ϕaccept :保证表格最后一行是 N N N 接受状态
(4) ϕ m o v e {\phi}_{move} ϕmove :保证相邻两行是合理的、满足 N N N 的转移函数的(所有合法窗口是可以枚举出来的)
分析:cell 和 move 的限定的长度为 O ( n 2 k ) O(n^{2k}) O(n2k) ,start 和 move 限定的长度为 O ( n k ) O(n^k) O(nk) ,即总的复杂度为 O ( n 2 k ) O(n^{2k}) O(n2k) ,并且 N N N 的任何一个分支就代表了 ϕ \phi ϕ 的一个赋值,以此实现了归约
Th 7.32: 3 S A T 3SAT 3SAT 是 N P NP NP 完全的
(只需要把刚刚的所有约束 ϕ c o n s t r a i n t \phi_{constraint} ϕconstraint 都分解为 3 n f 3nf 3nf 即可)
(重点关注3合取范式,之后证明 N P C NPC NPC 基本上是使用 3 S A T 3SAT 3SAT )
7.5 几个NP完全问题
理论:证明某个问题是 N P C NPC NPC ,基本上是借助NPC性质从 3 S A T 3SAT 3SAT 归约出来,因此要明白对于 ϕ \phi ϕ ,它的变量 x i x_i xi 应该归约为什么结构(变量构件),它的子句 c i c_i ci 又应该归约为什么结构(子句构件);
团问题
Th 7.33: C L I Q U E CLIQUE CLIQUE 是 N P NP NP 完全的
归约函数: f : ϕ → < G , k > f:{\phi}\to {\lt}G,k{\gt} f:ϕ→<G,k> , ϕ = ( a 1 ∨ b 1 ∨ c 1 ) ∧ ( a 2 ∨ b 2 ∨ c 2 ) ∧ . . . ∧ ( a k ∨ b k ∨ c k ) \phi=(a_1\vee b_1\vee c_1)\wedge(a_2\vee b_2\vee c_2)\wedge ... \wedge (a_k\vee b_k\vee c_k) ϕ=(a1∨b1∨c1)∧(a2∨b2∨c2)∧...∧(ak∨bk∨ck)
构造:将每个变量作为一个结点(可重复出现),将每个子句看成一个结点组,要求:
- 组内的结点没有边相连
- x i x_i xi 与 x i ‾ \overline{x_i} xi 没有边相连
其他能连的边都连起来。显然,该归约函数复杂性为 O ( k 2 ) O(k^2) O(k2) ,为多项式时间
那么,是否存在使 ϕ \phi ϕ 为1的赋值规约为 G G G 中是否存在 k k k 团:
① 若存在使 ϕ \phi ϕ 为1的赋值,则每一组中至少有一个变量被赋值为1,从中随意选择一个结点;由于这 k k k 个点来自不同的组,且 x i x_i xi 和 x i ‾ \overline{x_i} xi 不可能同时赋值为1,因此这 k k k 个点都有边相连,构成了一个 k k k 团
② 若 G G G 中存在 k k k 团,因为这 k k k 个点之间两两有边相连,因此这 k k k 个点必定来来自不同的组,且 x i x_i xi 和 x i ‾ \overline{x_i} xi 不可能同时出现在这 k k k 个点中;故让这几个点对应的变量赋值为1,即 ϕ \phi ϕ 中每个子句中至少有一个1,则得到了一个可以使 ϕ = 1 \phi=1 ϕ=1 的赋值
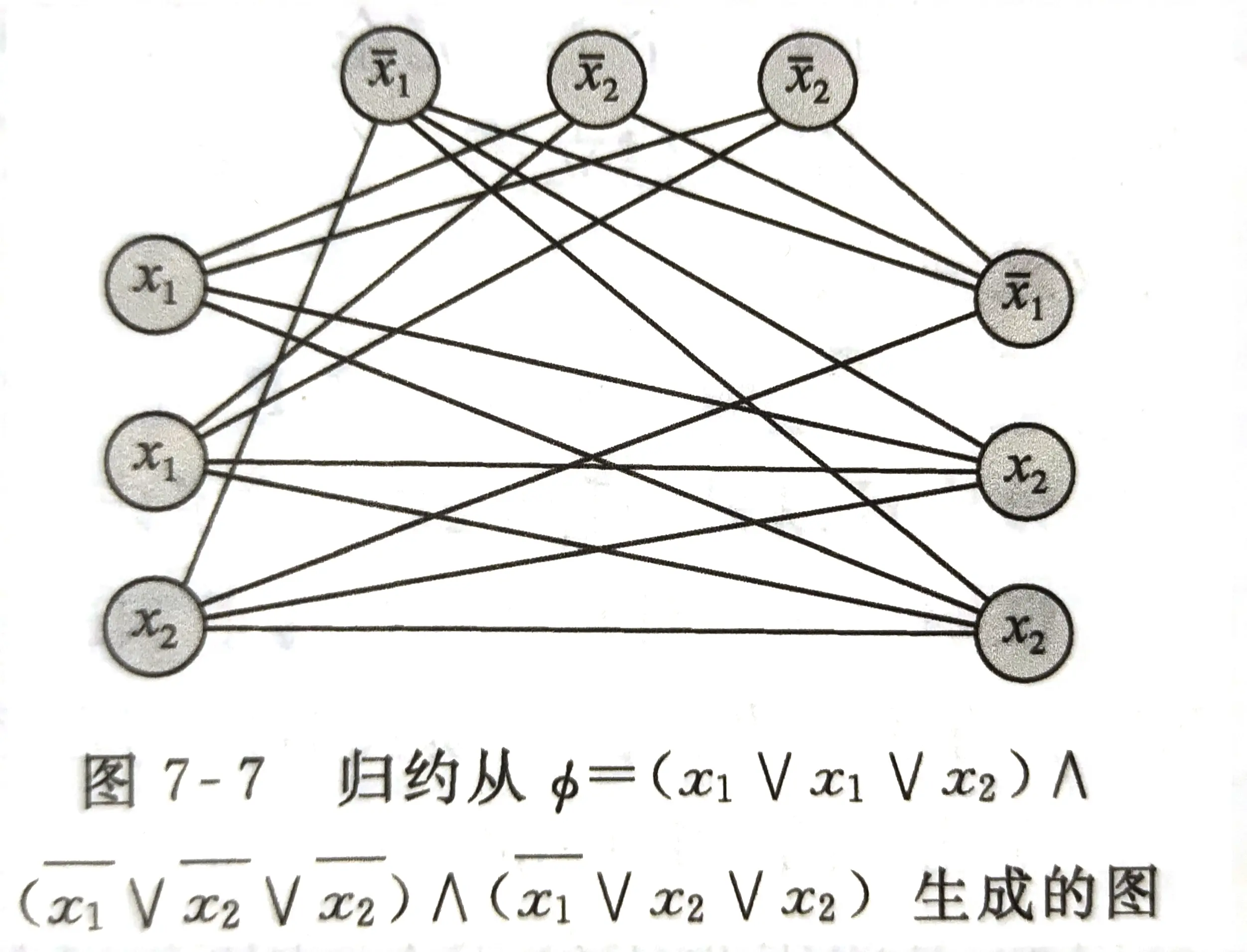
因此, 3 S A T ≤ P C L I Q U E 3SAT{\leq}_PCLIQUE 3SAT≤PCLIQUE , C L I Q U E CLIQUE CLIQUE 是 N P NP NP 完全的
顶点覆盖问题
Def: V E R T E X − C O V E R = { < G , k > ∣ G VERTEX-COVER=\{ {\lt}G,k{\gt}{\,}|{\,}G VERTEX−COVER={<G,k>∣G 是具有 k k k 个点的结顶点覆盖的无向图 } \} }
Th 7.34: V E R T E X − C O V E R VERTEX-COVER VERTEX−COVER 是 N P NP NP 完全的
归约函数: f : ϕ → < G , k > f:{\phi}\to {\lt}G,k{\gt} f:ϕ→<G,k> , ϕ = ( a 1 ∨ b 1 ∨ c 1 ) ∧ ( a 2 ∨ b 2 ∨ c 2 ) ∧ . . . ∧ ( a l ∨ b l ∨ c l ) \phi=(a_1\vee b_1\vee c_1)\wedge(a_2\vee b_2\vee c_2)\wedge ... \wedge (a_l\vee b_l\vee c_l) ϕ=(a1∨b1∨c1)∧(a2∨b2∨c2)∧...∧(al∨bl∨cl)
构造:将所有变量的正反都作为结点加入(变量构件),将每个子句看成一个结点组(子句构件),要求:
- 每一组中的结点两两相连
- 变量构件的两个结点也有边相连
- 将变量构件与子句结点组中相同的变量的结点连接起来
该归约函数复杂性为 O ( k l ) O(kl) O(kl) ,为多项式时间

那么,是否存在使 ϕ \phi ϕ 为1的赋值规约为 G G G 中是否存在 k k k 个结点的覆盖:
① 若存在使 ϕ \phi ϕ 为1的赋值,则每一组中至少有一个变量被赋值为1,从中随意选择一个结点;将正反变量组中赋值为1的结点加入覆盖集,将子句结点组中除了赋值为1的结点的另外两个结点加入覆盖集;则
-
a. 变量构件的一条边被覆盖
-
b. 子句结点组中三条边都被覆盖
-
c. 二者之间的边也被覆盖
即构成了一个 k k k 个结点的覆盖
② 若 G G G 中存在 k k k 个结点的覆盖,则
- a. 变量构件中的一条边要被覆盖,必有 x i x_i xi 与 x i ‾ \overline{x_i} xi 中的一个加入了 k k k ;
- b. 子句结点组中的三条边必须要两个结点覆盖;
- c. 若变量构件中被选中的结点在子句结点组中也被选中,则该覆盖的结点显然超过 k k k 个,因此每个顶点覆盖均包含每个变量构建的一个结点和每个子句构件的两个结点,且子句构件中没有被选中的那个结点变量在构件中被选中,一共是 k k k 个结点;
将变量构件中被选中的结点对应的变量赋值为1,则得到了一个可以使 ϕ = 1 \phi=1 ϕ=1 的赋值
因此, 3 S A T ≤ P V E R T E X − C O V E R 3SAT{\leq}_PVERTEX-COVER 3SAT≤PVERTEX−COVER , V E R T E X − C O V E R VERTEX-COVER VERTEX−COVER 是 N P NP NP 完全的
(这里没有提及,可以思考一下 k k k 是什么呢?)
哈密顿路径问题
Th 7.35: H A M P A T H − C O V E R HAMPATH-COVER HAMPATH−COVER 是 N P NP NP 完全的
归约函数: f : ϕ → < G , s , t > f:{\phi}\to {\lt}G,s,t{\gt} f:ϕ→<G,s,t> , ϕ = ( a 1 ∨ b 1 ∨ c 1 ) ∧ ( a 2 ∨ b 2 ∨ c 2 ) ∧ . . . ∧ ( a k ∨ b k ∨ c k ) \phi=(a_1\vee b_1\vee c_1)\wedge(a_2\vee b_2\vee c_2)\wedge ... \wedge (a_k\vee b_k\vee c_k) ϕ=(a1∨b1∨c1)∧(a2∨b2∨c2)∧...∧(ak∨bk∨ck)
(有 l l l 种变量和 k k k 个子句)该归约函数复杂性为 O ( k l ) O(kl) O(kl) ,为多项式时间
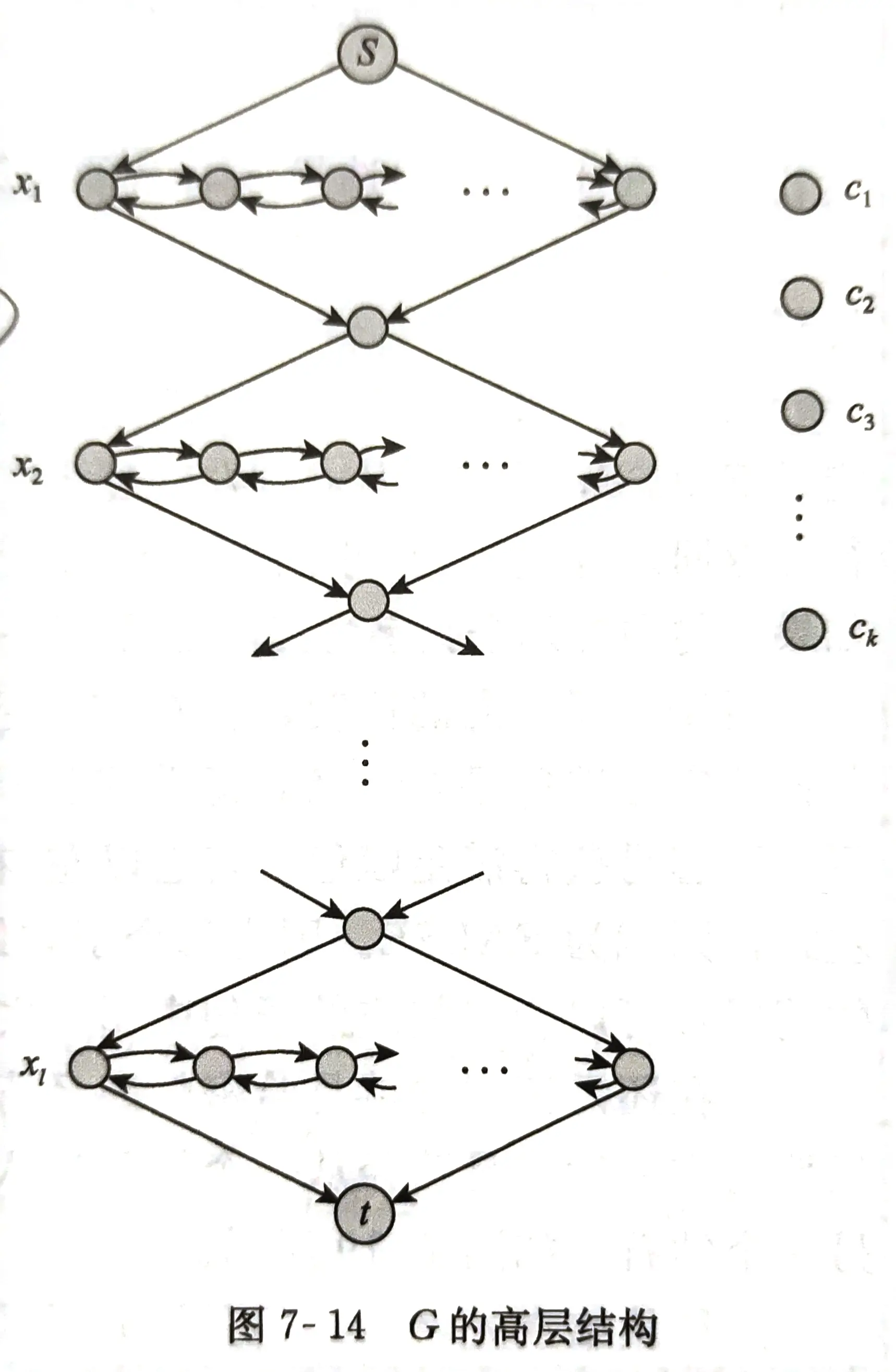
构造:将所有变量表示为钻石型结构(变量构件),将每个子句看成一个结点(子句构件),要求:

- 每个钻石中对应每个子句的为结点对,中间也被结点隔开,也就是一个钻石除了上下结点外,中间有 3 k + 1 3k+1 3k+1 个结点(图7-15)
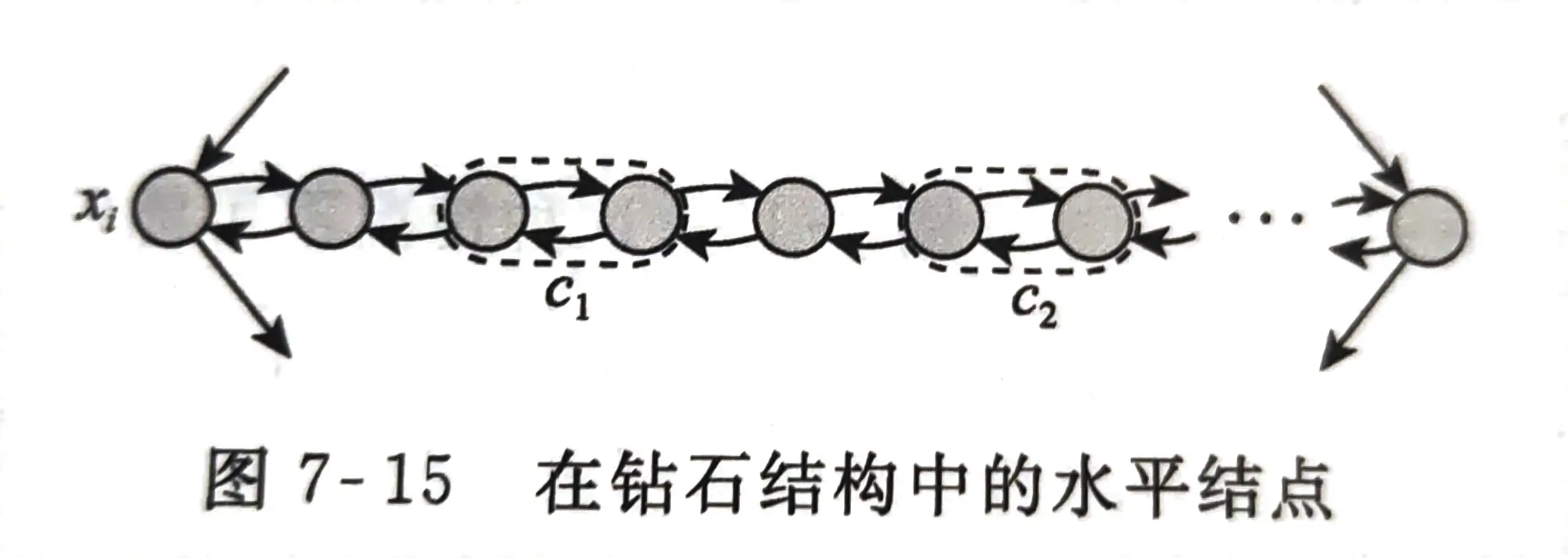
-
上下有 s s s 和 t t t 结点,串接所有 x i x_i xi 的钻石结构(图7-14)
-
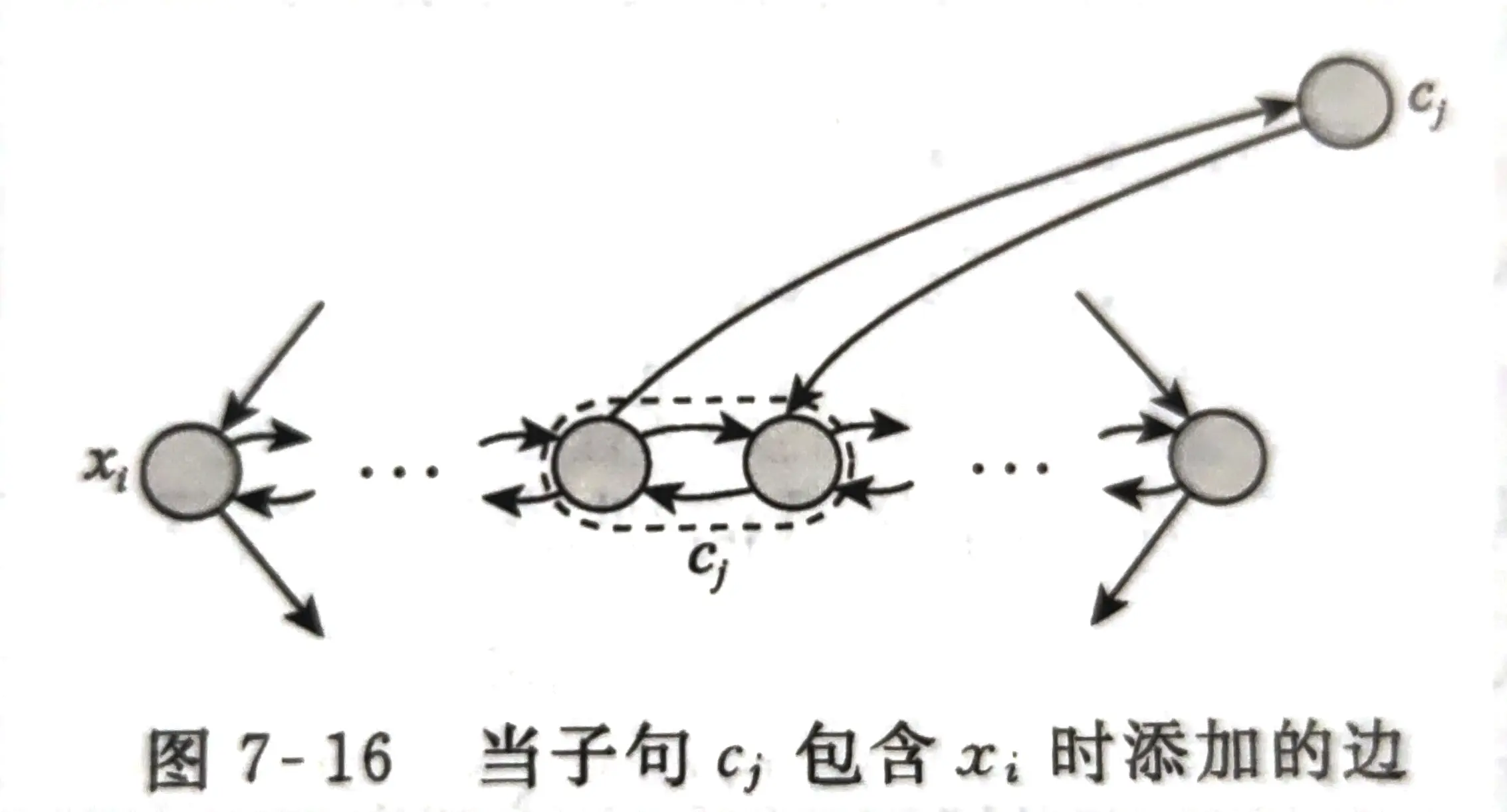
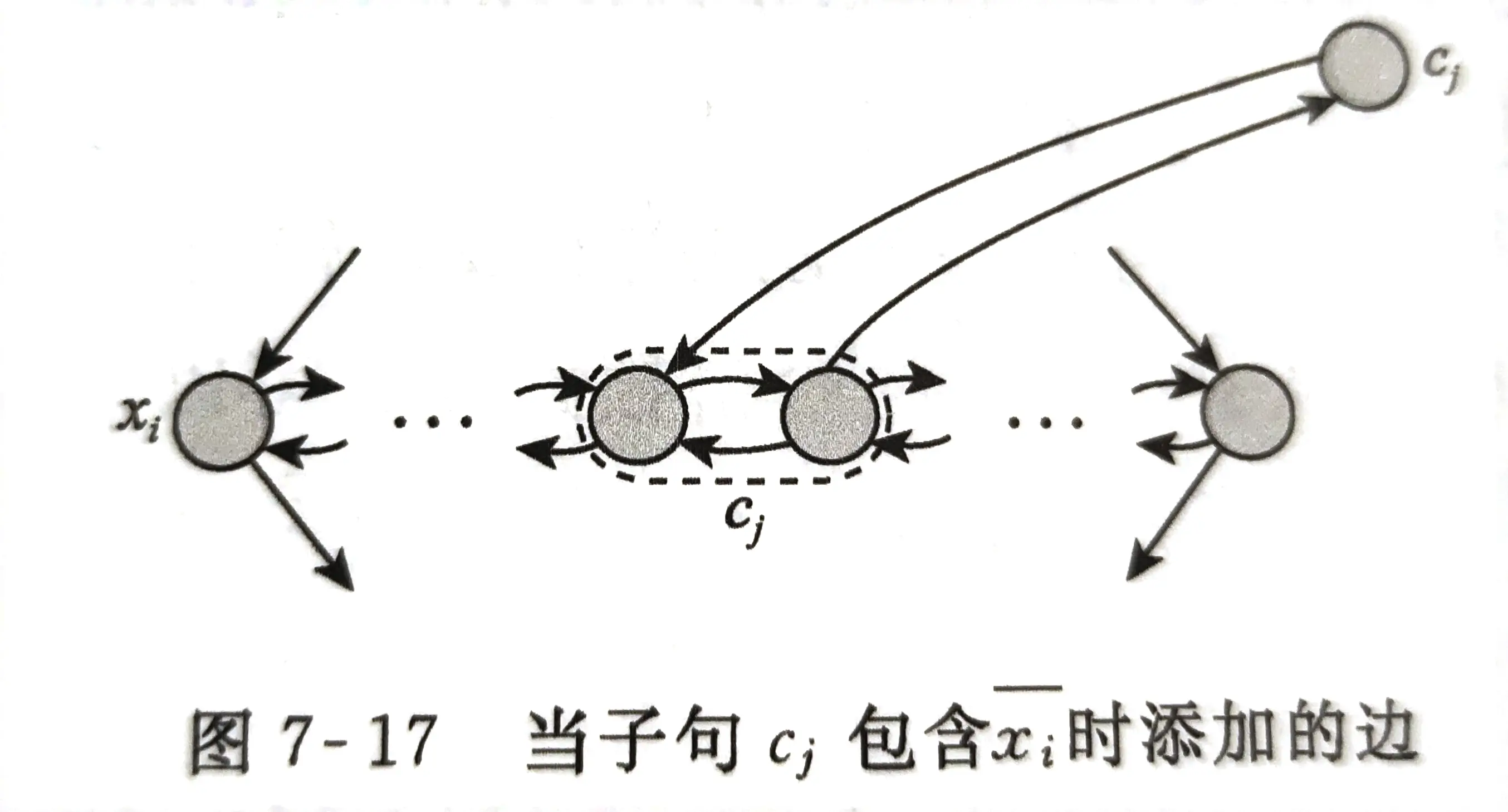
c i c_i ci 连接对应变量 x i x_i xi 的钻石的横向的结点对;根据 c i c_i ci 包括wether x i x_i xi or x i ‾ \overline{x_i} xi ,连接子句结点的方向不同:(图7-16)(图7-17)
 |  |
 |
那么,是否存在使 ϕ \phi ϕ 为1的赋值归约为 G G G 中是否存在哈密顿路径:
① 若存在使 ϕ \phi ϕ 为1的赋值,则从图中的 s s s 点开始,从上至下,遍历每个钻石型结构;若 x i x_i xi 被赋值为1,则 x i x_i xi 对应的钻石型从右到左遍历,否则从左到右遍历;每一组中至少有一个变量被赋值为1,从中随意选择一个结点;横向遍历钻石时,每次遇到能够分支到 c i c_i ci 的路径,就往分支的方向过去把 c i c_i ci 遍历了;
-
每一组中至少有一个变量被赋值为1,因此 c i c_i ci 一定会被遍历到
-
由于每组只选了一个结点,因此 c i c_i ci 不会被重复遍历
即构成了一个哈密顿路径
② 若 G G G 中存在哈密顿路径,则:只能和 ① 中的路径一样,唯一违法该规则的途径是:
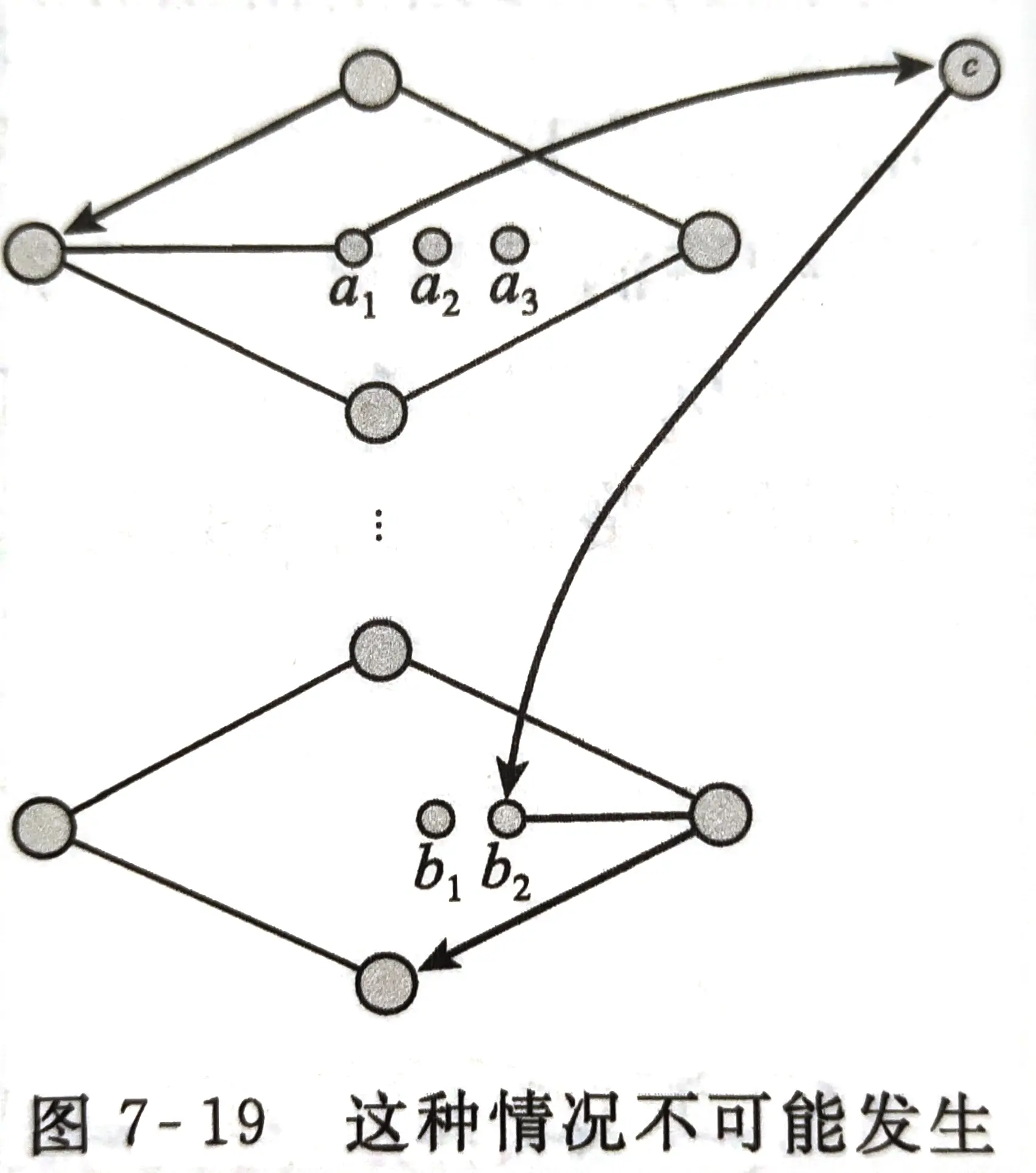
不过,如果这样的话,中间被跳过的结点想要再次被遍历的话,就会重复遍历一些结点,因此不存在这种情况。即哈密顿路径一定是满足 ϕ \phi ϕ 的赋值条件的,对于 x i x_i xi 的钻石型,若从右到左遍历则将 x i x_i xi 赋值为1,否则赋值为0;这样,每个 c i c_i ci 至少会被某个钻石遍历到,因此说明每个子句中至少有一个变量为1,可得 ϕ = 1 \phi=1 ϕ=1
因此, 3 S A T ≤ P H A M P A T H 3SAT{\leq}_PHAMPATH 3SAT≤PHAMPATH , H A M P A T H HAMPATH HAMPATH 是 N P NP NP 完全的
Def: U H A M P A T H UHAMPATH UHAMPATH 指无向图中的哈密顿路径问题
Th 7.36: U H A M P A T H − C O V E R UHAMPATH-COVER UHAMPATH−COVER 是 N P NP NP 完全的
对某个有向图 G G G ,其是否存在哈密顿路径 < G , s , t > {\lt}G,s,t{\gt} <G,s,t> ,归约为无向图 G ′ G' G′ 中是否存在哈密顿路径 < G ′ , s o u t , t i n > {\lt}G',s^{out},t^{in}{\gt} <G′,sout,tin>,其中:
- s o u t = s s^{out}=s sout=s , t i n = t t^{in}=t tin=t
- 其余结点 u u u 分解为三个结点 u i n , u m i d u^{in},u^{mid} uin,umid 和 u o u t u^{out} uout ,其中 u i n , u m i d u^{in},u^{mid} uin,umid 有边相连, u m i d , u o u t u^{mid},u^{out} umid,uout 有边相连
- 若原来有向图中有 v → u v\to u v→u ,现在无向图中有 v o u t , u i n v^{out},u^{in} vout,uin 有边相连
则:
① G G G 的哈密顿路径即为 G ′ G' G′ 中的哈密顿路径
② 对于 G ′ G' G′ 中的哈密顿路径,由于从 s o u t s^{out} sout 出发,对于某个 u m i d u^{mid} umid ,只能是: u i n → u m i d → u o u t u^{in}\to u^{mid}\to u^{out} uin→umid→uout ,因此可以对应于 G G G 中的哈密顿路径
因此, H A M P A T H ≤ P U H A M P A T H HAMPATH{\leq}_PUHAMPATH HAMPATH≤PUHAMPATH , U H A M P A T H UHAMPATH UHAMPATH 是 N P NP NP 完全的
子集和问题
Th 7.37: S U B S E T − S U M SUBSET-SUM SUBSET−SUM 是 N P NP NP 完全的
归约函数: f : ϕ → < S , t > f:{\phi}\to {\lt}S,t{\gt} f:ϕ→<S,t> , ϕ = ( a 1 ∨ b 1 ∨ c 1 ) ∧ ( a 2 ∨ b 2 ∨ c 2 ) ∧ . . . ∧ ( a k ∨ b k ∨ c k ) \phi=(a_1\vee b_1\vee c_1)\wedge(a_2\vee b_2\vee c_2)\wedge ... \wedge (a_k\vee b_k\vee c_k) ϕ=(a1∨b1∨c1)∧(a2∨b2∨c2)∧...∧(ak∨bk∨ck)
(有 l l l 种变量和 k k k 个子句)该归约函数复杂性为 O ( ( k + l ) 2 ) O((k+l)^2) O((k+l)2) ,为多项式时间
这个构造有点难理解:
- 变量构件:每个 x i x_i xi 表示为两个十进制大整数 y i y_i yi 和 z i z_i zi ,例如图中 y 1 = 10...010...0 y_1=10...010...0 y1=10...010...0 ,前面一个 10... 10... 10... 一共 l l l 位,后边一个 10... 10... 10... 一共 k k k 位
- 子句构件:每个子句 c i c_i ci 代表 y j y_j yj 或 z j z_j zj 的某一位是0或1:若 c i c_i ci 中有 x j x_j xj,则 y j y_j yj 对应那位为1, z j z_j zj 对应那位为0;若 c i c_i ci 中有 x j ‾ \overline{x_j} xj,则 y j y_j yj 对应那位为0, z j z_j zj 对应那位为1;否则都为0
将目标和 t t t 处理为大整数 1...13...3 1...13...3 1...13...3 的形式,一共 l l l 个 1 1 1 和 k k k 个 3 3 3 ;构造集合 S S S 为所有的 y i y_i yi 和 z i z_i zi ,再加上一些 g i g_i gi 和 h i h_i hi ,其中 g k = h k = 10...0 g_k=h_k=10...0 gk=hk=10...0,一共 k k k 位;

那么,是否存在使 ϕ \phi ϕ 为1的赋值归约为 S S S 中是否存在和为目标和 t t t 的子集:
① 若存在使 ϕ \phi ϕ 为1的赋值,则
- 对于变量 x i x_i xi ,若赋值为1,则将 y i y_i yi 加入子集,否则将 z i z_i zi 加入子集;保证了子集和在该位的值为1
- 此时由于每个 c i c_i ci 中至少有一个变量被赋值为1,因此 c i c_i ci 对应的那位至少有1个 1 1 1 ;若该位的和小于 3 3 3 ,则显然可通过适当添加 g i g_i gi 和 h i h_i hi 来使子集和在该位的值为 3 3 3
由此构造出了一个子集,其中的和等于目标和 t t t
② 若 S S S 中存在一目标和为 t t t 的子集:
- 对于前 t t t 的前 l l l 位,为了保证每一位都是1,必有 y i y_i yi 和 z i z_i zi 中的某一个在该子集当中;
- 对于前 t t t 的后 k k k 位,为了保证每一位都是3,即使 g i g_i gi 和 h i h_i hi 加上去了,和也只有2,因此 c i c_i ci 在该位至少有一个1被选中,即子句中至少有一个变量被赋值为1
对于 x i x_i xi ,若 y i y_i yi 存在于该子集当中,则对其赋值为1,否则赋值为0;得到了一个可以使 ϕ = 1 \phi=1 ϕ=1 的赋值























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










