计算理论 第7章 复杂性理论 II NP类问题

计算理论导引 第7章 复杂性理论 II 的相关笔记，包括：NP类问题……

这部分重点内容在于，对于一个NP问题，如何构造它的多项式时间验证机合非确定的多项式时间判别机。

第7章笔记 （II）

7.3 NP 类

验证机与判别机

验证机（Verifier）

两个 $NP$ 问题：

• H A M P A T H = { < G , s , t >   ∣   G HAMPATH=\{ {\lt}G,s,t{\gt}{\,}|{\,}G HAMPATH={<G,s,t>∣G 是包含从 $s$ 到 $t$ 的哈密顿路径的有向图 $\}$ （恰好经过每个顶点一次）
• C O M P O S I T E S = { x   ∣   x = p q , COMPOSITES=\{x{\,}|{\,}x=pq, COMPOSITES={x∣x=pq, 整数 $p,q>1\}$ （合数问题）

特点：无法在多项式时间内求解，但是对于某个具体的例子，可以在多项式时间内验证

Def 7.15：语言 $A$ 的 验证机 是一个算法 $V$ ，这里：

A = { w   ∣   对 某 个 字 符 串   c ， V   接 受 < w ,   c > } A=\{w{\,}|{\,}对某个字符串{\,}c，V{\,}接受{\lt}w,{\,}c{\gt}\} A={w∣对某个字符串c，V接受<w,c>}

• 多项式时间验证机：在 $w$ 的长度的多项式时间内运行
• 多项式可验证的：若语言 $A$ 有一个多项式时间验证机，则称它为多项式可验证的
• $c$ 称为 $A$ 的成员资格 证书 或 证明

（验证机 $V$ 根据证书 $c$ 来验证 $w$ 是否为 $A$ 的成员，因此多项式时间验证机的证书长度具有 $w$ 长度的多项式长度，并且对于具体的 $w$ ，$c$ 是具体的，并不是一成不变的）

对于上面列举的两个问题，其证书分别为：

• 字符串 $<G,s,t>\in HAMPATH$ 的证书就是从一条从 $s$ 到 $t$ 的哈密顿路径
• 对问题 $COMPOSITES$ ，合数 $x$ 的证书为其一个因子

Def 7.16：$NP$ 是具有多项式时间验证机的语言类

判定机（Decider）

$NP$ ：非确定型多项式时间（nondeterministic polynomial time）<span id="HAMPATH">

$HAMPATH$ 问题 $N_1=$ “对输入 $<G,s,t>$ ，这里 $G$ 是包含节点 $s$ 和 $t$ 的有向图”，构造一个非确定型图灵机（$NTM$）：

① 写一列 $m$ 个数 $p_1,p_2,...p_m$ ，$m$ 是图 $G$ 的结点数， $p_i\in N$ 且 $p_i\in [1,m]$

② 检查数列 $p_i$ 重复性，若发现有重复，则 拒绝

③ 检查 $s=p_1$ 和 $t=p_m$ 是否都成立，若有一个不成立，则 拒绝

④ 检查边 $(p_i,p_{i+1})$，$i\in [1,m-1]$ 是否属于图 $G$ 中，若有其中一条边不成立，则 拒绝

分析：① - ④ 的每一步在多项式时间内可完成，于是此算法在非确定型图灵机的多项式时间内可完成

Th 7.17 ：一个语言在 $NP$ 中 $⟺$ 它能被某个非确定型多项式时间图灵机判定

左到右：

设 $A\in NP$，已知存在多项式时间验证机 $V$ ，假设 $V$ 在时间 $n^k$ 内运行，要构造一 $NTM$ $N$ 可判定 $A$ ，构造如下：对于长为 $n$ 的输入 $w$ ，

① 非确定地选择最长为 $n^k$ 的字符串 $c$ 作为证书

② 在 $V$ 上运行 $<w,c>$

③ 若 $V$ 接受，则 <em>接受</em> ；否则 <em>拒绝</em>

（选择证书 $c$ 的长度为 $n^k$ ，是因为 $V$ 最多处理长度为 $n^k$ 长度的字符串）

右到左：

已有一 $NTM$ $N$ 可判定 $A$ ，要构造多项式时间验证机 $V$ 如下：对输入 $<w,c>$ ,

① 在 $N$ 上运行 $w$ ，但把 $c$ 中每一个字符看作每一步所做的非确定性选择的描述

② 若 $N$ 当前计算分支接受，则 <em>接受</em> ；否则 <em>拒绝</em> ；

（证书 $c$ 其实就代表了非确定型图灵机对于输入 $w$ 的一个分支，也就是此时的 $NTM$ 实际上是 $DTM$）

Def 7.18：定义 $NTIME(t(n))$ 为被 $O(t(n))$ 时间的非确定型图灵机所判定的语言集合

Th 7.19：$NP={\cup }_{k}NTIME(n^k)$

（所有非确定型计算模型都是多项式等价的，因此 $NP$ 对具体计算模型的选择不敏感）

（非确定型计算模型的某一具体分支是多项式时间内可完成的，所以总的来说也是多项式时间内可完成的；但是转化为确定的单带图灵机就需要指数时间了）

（大家要关注decider和verifier的区别，判别机对应验证机）

NP 问题举例

团（Clique）

Def：团 为一个无向图中的完全子图，k团 为包含 $k$ 个节点的团

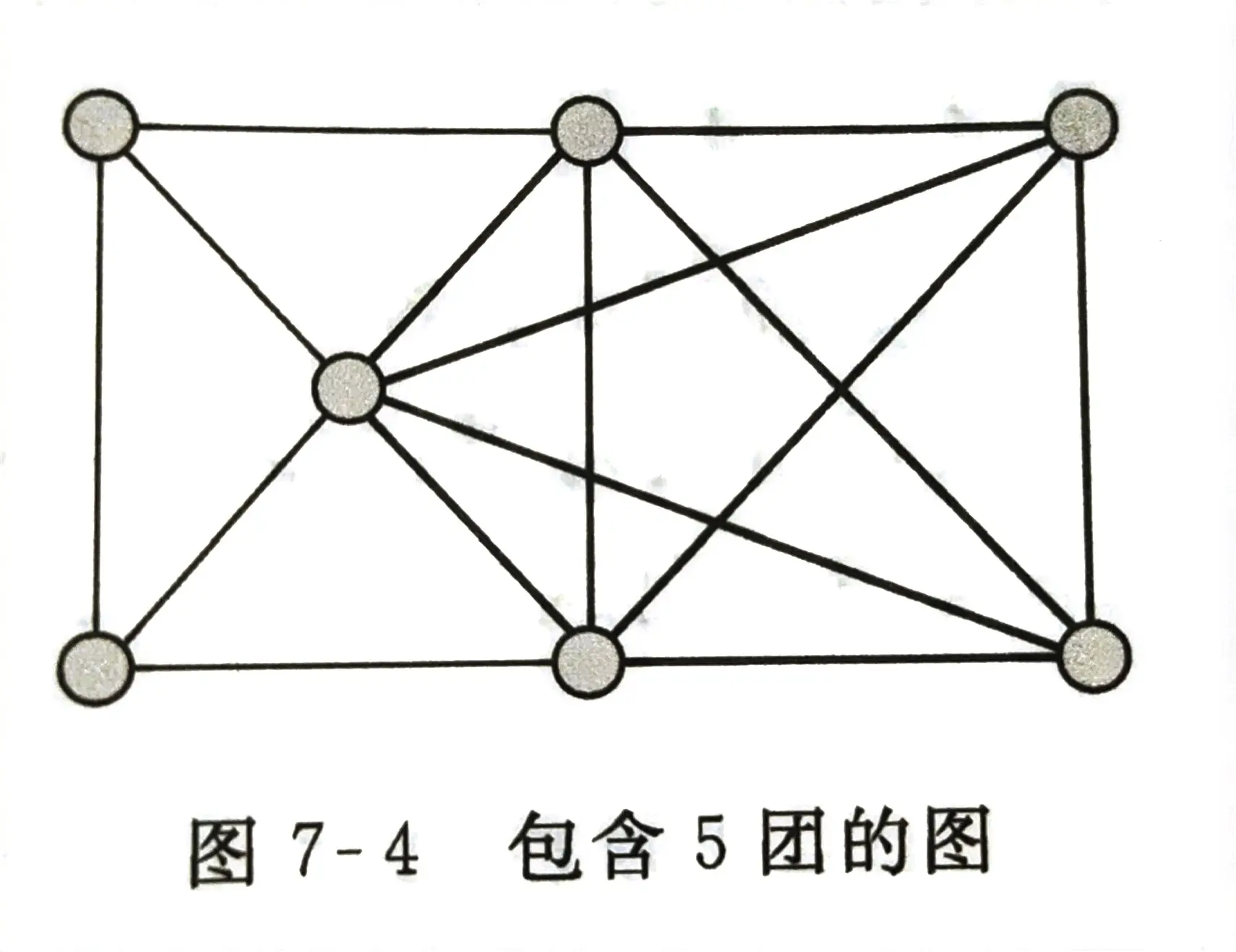
Def： C L I Q U E = { < G , k >   ∣   G CLIQUE=\{ {\lt}G,k{\gt}{\,}|{\,}G CLIQUE={<G,k>∣G 是包含 $k$ 团的无向图 $\}$

Th 7.20： $CLIQUE\in NP$

思路：可以构造多项式时间的验证机来证明，也可以构造多项式时间的非确定型判定机来证明

证法一：构造验证机 $V$ ，对于输入 $<<G,k>,c>$ ，（证书 $c$ 即为团）

① 检查 $c$ 中是否有 $k$ 个节点，且都属于 $G$ ；

② 检查 $c$ 中所有边是否都在 $G$ 中

③ 若两项检查都通过，则 <em>接受</em> ；否则 <em>拒绝</em> ；

分析：两项检查都与 $G$ 的点数或边数的多项式相关

证法二：构造判定机器 $N$ ，对于输入 $<G,k>$，

① 非确定地从 $G$ 中选择带有 $k$ 个节点的子图 $c$；

② 检查 $G$ 中是否包含 $c$ 中所有结点两两相连的边；

③ 若通过 ② ，则 <em>接受</em> ；否则 拒绝 ；

分析：① 中的选择有点像是上边 $HAMPATH$ 问题的 ①

目标和子集

Def： S U B S E T − S U M = { < x , t >   ∣   s = { x 1 , x 2 , . . . , x k } SUBSET-SUM=\{ {\lt}x,t{\gt}{\,}|{\,}s=\{x_1,x_2,...,x_k\} SUBSET−SUM={<x,t>∣s={x1​,x2​,...,xk​} 且存在 { y 1 , y 2 , . . . , y l }   ⊆   s \{y_1,y_2,...,y_l\}{\,}{\subseteq}{\,}s {y1​,y2​,...,yl​}⊆s 使得 $\Sigma y_i=t\}$

Th 7.21：$SUBSET-SUM\in NP$

思路：可以构造多项式时间的验证机来证明，也可以构造多项式时间的非确定型判定机来证明

证法一：构造验证机 $V$ ，对于输入 $<<S,t>,c>$ ，（证书 $c$ 即为某个子集）

① 检查 $c$ 中的和是否为 $t$

② 检查 $S$ 中是否不重复地包含 $c$ 中所有数

③ 若两项检查都通过 ，则 <em>接受</em> ；否则 <em>拒绝</em> ；

分析：两项检查都与 $S$ 的元素个数的多项式相关

证法二：构造判定机器 $N$ ，对于输入 $<S,t>$，

① 非确定地从 $S$ 中选择一个子集 $c$；

② 检查 $c$ 中的和是否为 $t$；

③ 若通过 ② ，则 <em>接受</em> ；否则 <em>拒绝</em> ；

注意：$coNP$ 为 $NP$ 中的语言的补语言，目前还无法知道二者的差别

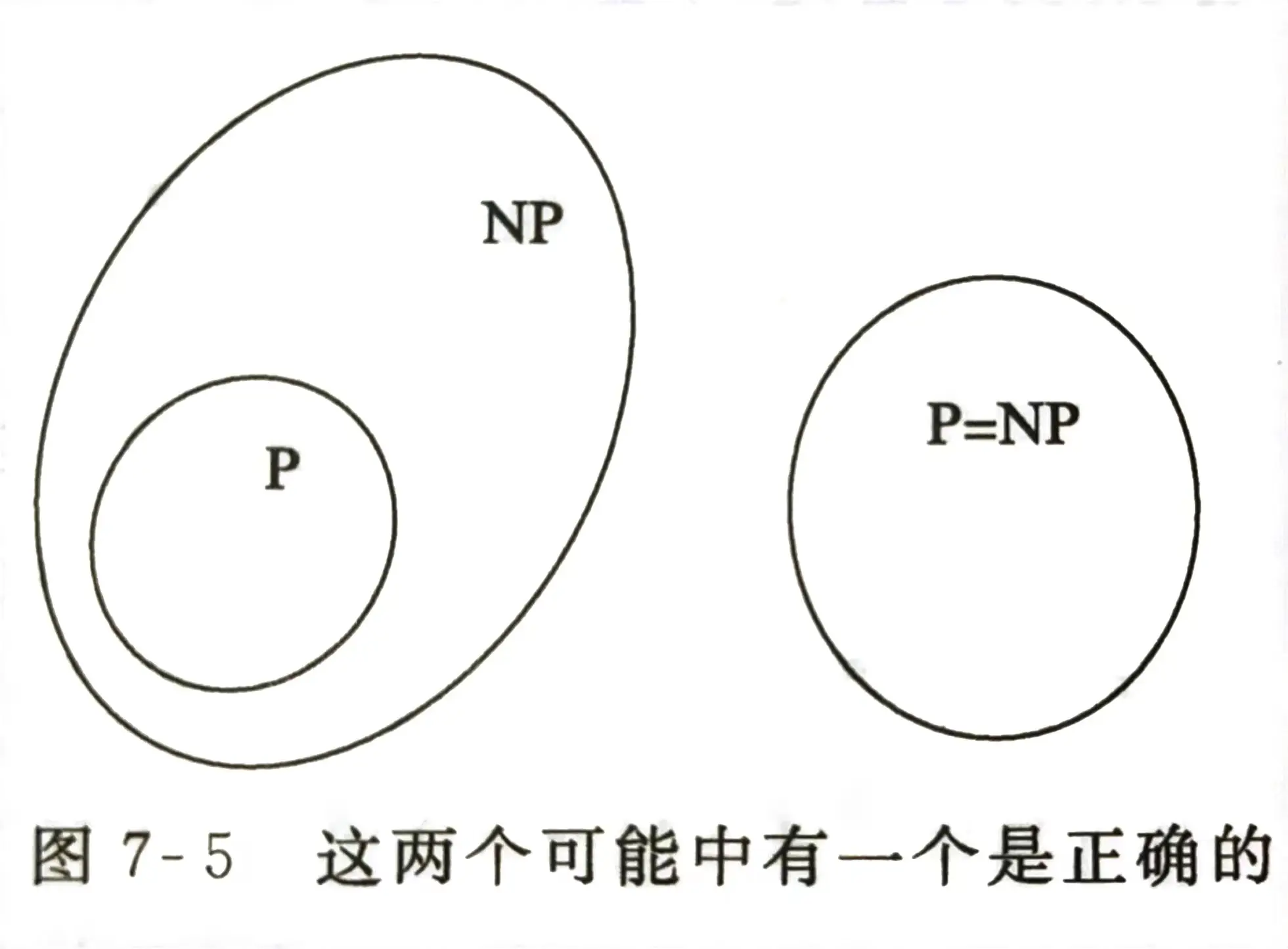
P 与 NP 问题

$P=$ 成员资格可以快速 判定 的语言类

$NP=$ 成员资格可以快速 验证 的语言类

P类问题和NP类问题有精确定义：

P类问题	NP类问题
确定型图灵机判别	非确定型图灵机判别

目前已知最好判定语言是 $NP$ 的确定型方法使用指数时间，只能证明

$$NP\subseteq EXPTIME={\cup }_{k}TIME(2^k)$$

但是无法判定是否 $P?=NP$