[DFT]什么是Voltage Data Retention(VDR)

什么是VDR/DRV

Data retention voltage could be explained as the lowest possible power supply voltage at which the data can be retained inside the SRAM.
One thing to remember is that the chip is deselected at this point of time.

即，在SRAM处于standby 模式下，需要维持SRAM中的data不变所需要提供的最低的供电电压。

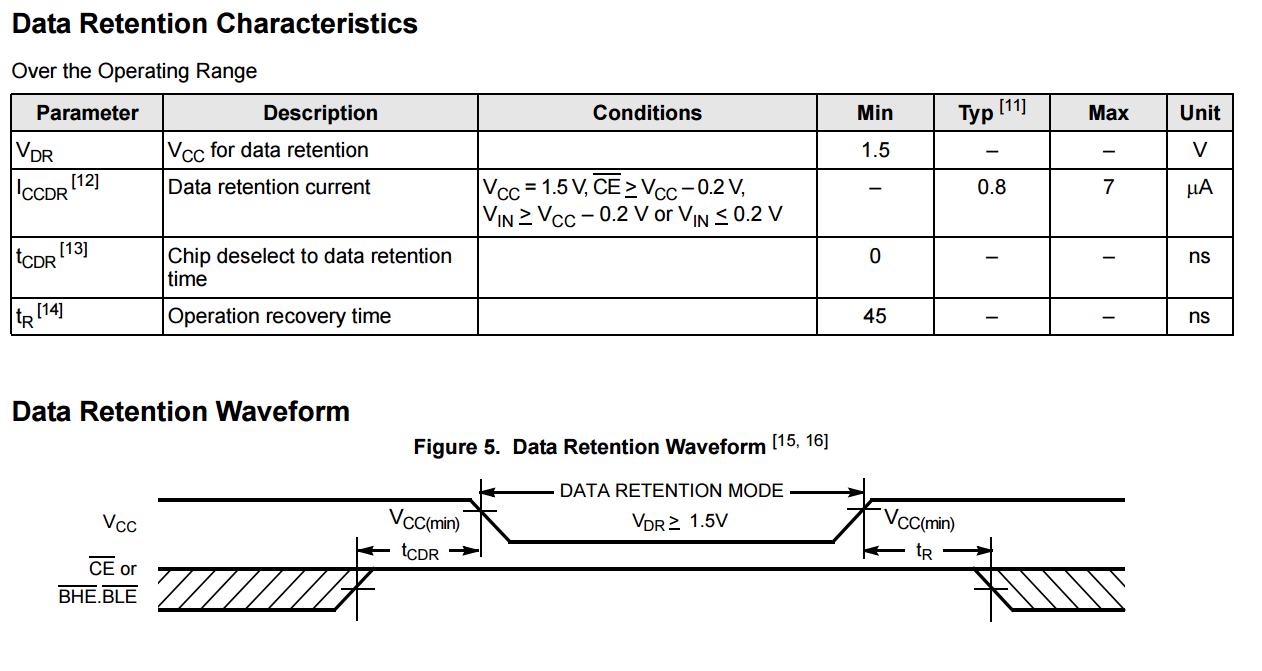
data retention主要涉及4个指标：
1. VCC for data retention
2. Data retention current
3. Chip deselect to data retention time
4. Operation recovery time

下面是一些芯片厂商的datasheet中，对data retention的定义：

• 芯片1
  

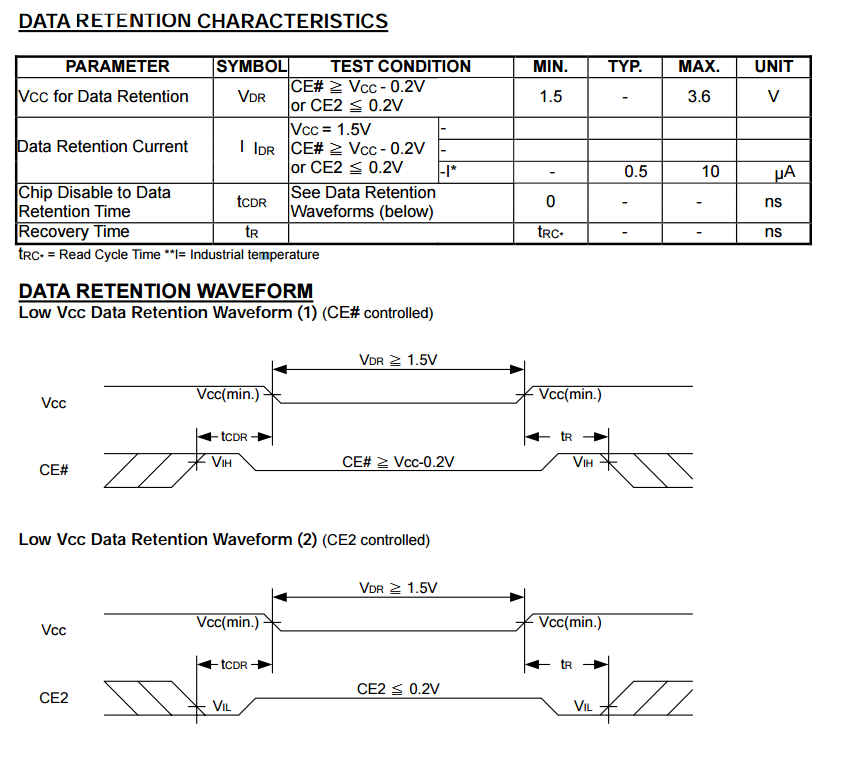
• 芯片2
  

• 芯片3