机器学习python实践中关于数据预处理——“数据白化”的一些个人思考

最近在利用python对机器学习进行实践，但是在实践过程中遇见了“数据白化”，查了一些资料，都在说“数据白化”可以降低数据的特征之间的相关性，都在说使用PCA求出特征向量，然后把数据X映射到新的特征空间，这样的一个映射过程就是可以降低数据之间的相关性，整个人真的很懵，为啥数据只是换了一个坐标空间表示，就可以降低特征之间的相关性？查了很多资料，然后这篇文章主要想记录并分享一下个人心得。当然，如果这篇文章还能入得了各位“看官”的法眼，麻烦点赞、关注、收藏，支持一下！

要搞明白“为啥数据只是换了一个坐标空间表示，就可以降低特征之间的相关性？”这个问题，必须先知道“相关性”指的是什么？

先给出“相关性”的定义：

可能看了定义，很多小伙伴单单将“相关性”拎出来是明白的，但是真的要带回到我们的问题中，就又懵逼了，所以本人给出一个“私人浓缩”版的定义：数据的不同特征之间存在相关性指的是不同特征的变化趋势一致或者相反

下面我重点解释一下““相关性”的私人浓缩”版定义：

为了探索变化趋势是否一致，我们需要引入“期望”、“协方差”等概念来帮助我们判断特征的变化趋势。

要想知道数据某一特征的的变化趋势必须需有一个参照才行，而特征的“期望”就给我们提供了这个参照，我们可以通过比较特征值与其期望值的大小来判断特征的变化趋势，当特征值大于期望值时特征值有变大的趋势，当反之，特征值就有变小的趋势。

至于为什么将“期望”作为参照本人只能给出一个比较偏门的解释：可能很多人如果将上一时刻的数据点拿来当作参照，即在时间刻度上观察数据的变化，是非常容易理解的，但是在采样过程中我们拿到手的可能是一团数据，并不知道每个数据点的时间点对照，所以很多时候无法将上一时刻的数据点拿来当参照，而“期望”却可以。因为“期望”可以简单的看做所采样本的均值，且在机器学习中我们是认为事物发展是存在内在规律的，所以期望值是一个定值，随着采样数目的增多，样本的均值也会越接近“期望”，所以采样的数据一定是在期望值的上下浮动，因此，我们就可以将“期望”当作一个参照，一个锚点

那么该如何比较不同特征之间的变化趋势呢？——我的答案是：“协防差”。

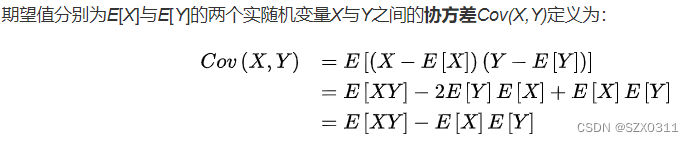
 上面的图片给出了“协方差”公式定义，下面我将这条公式一层层拨开来向大家说明，为什么“协方差”可以比较不同特征之间的变化趋势：

先不看协方差公式最外层的期望，仅先看里层的(X-E[X])(Y-E[Y])公式，根据上面说到的，我们可以比较特征与期望的大小来判断该特征的变化趋势，那么(X-E[X])就可以判断特征X的变化趋势，(Y-E[Y])就可以判断特征Y的变化趋势，而两者的乘积就可以帮助我们判断两者的变化趋势是否一致，如果两者的乘积是大于零的，则表示两者变化趋势相同，如果两者乘积小于零，则表示两者的变化趋势相反，如果两者乘积为零，则无法判断两者的变化趋势。之所以当两者乘积为零时无法判断两者的变化趋势，是因为(X-E[X])(Y-E[Y])所比较的“变化趋势”都是一个点的变化趋势，但是我们要比较的是整体的“变化趋势”，所以我们要对(X-E[X])(Y-E[Y])求期望，即求Cov(X,Y)，从而判断特征X和特征Y的总体变化趋势是否一致。由此，我们就可以得出如下结论：

①当Cov(X,Y)＞0，X和Y变化趋势一致，即正相关

②当Cov(X,Y)＜0，X和Y变化趋势相反，即负相关

③当Cov(X,Y)=0，X和Y之间不相关

通过上述的分析，我们清楚的解释了“相关性”的定义，同时给出了不同特征之间的“相关性”的衡量指标——“协方差”，我们可以通过判断“协方差”的正负性来判断不同特征之间是否相关。

“相关性”阐述清楚后，回到最初的问题“为啥数据只是换了一个坐标空间表示，就可以降低特征之间的相关性？”

下面结合互联网大佬的图片给大家解释一下我们所提出的问题：

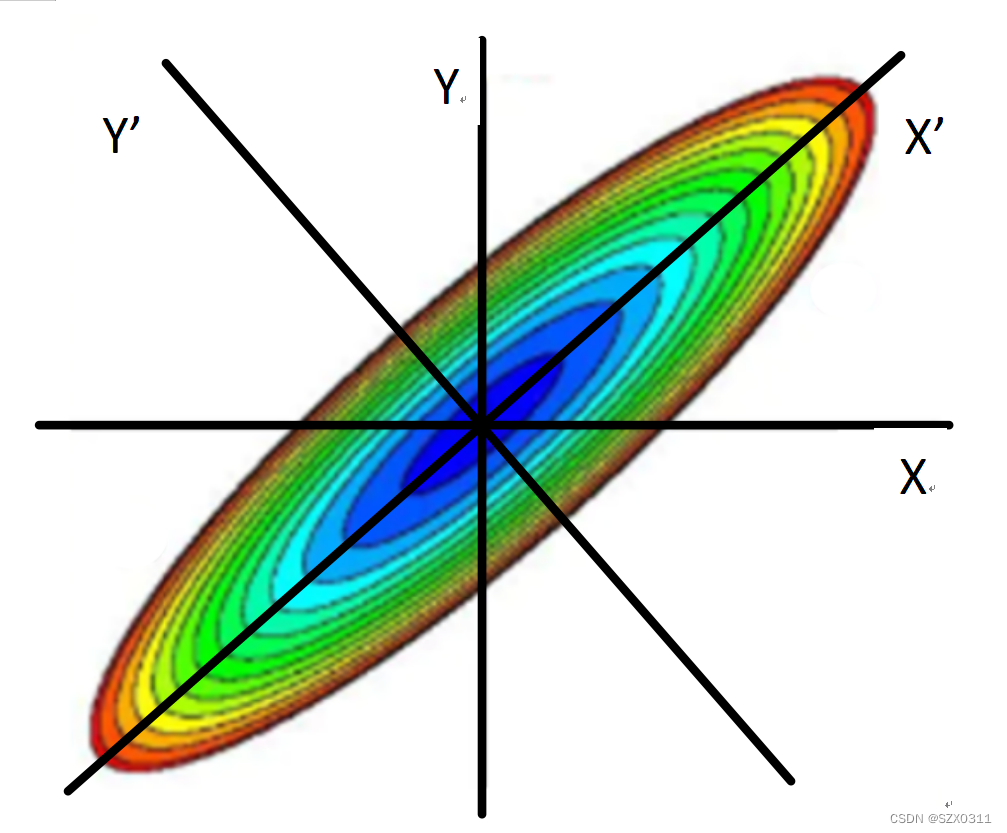
如上图所示，坐标轴X和Y共同构成原始坐标空间，坐标轴X'和Y'共同新坐标空间，数据点构成的云图为一个椭圆，同时，不难发现，两个坐标空间的原点重合，不管在哪个坐标空间中数据点构成的椭圆形云图均关于原点中心对称，且数据点的两个特征的均值都是零，即在原始坐标空间中 ， 在新坐标空间中，所以可以得到，不管在哪个坐标空间中，两特征的期望均为零，即  

为了更只直观的展示，我将上图中的云图拆成如下图所示，其中左图为原始坐标空间，右图为新坐标空间：

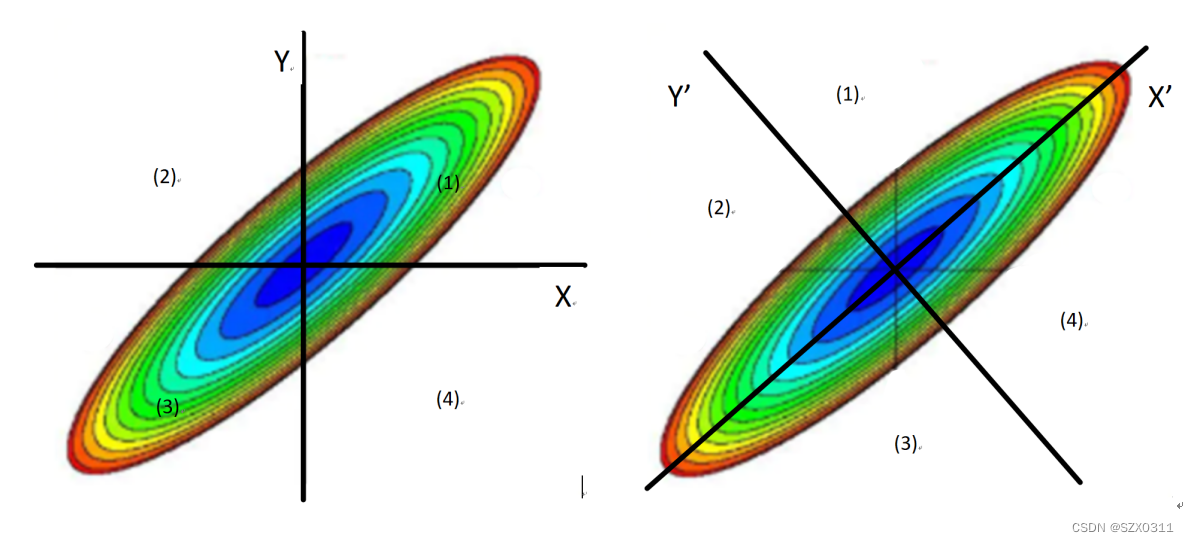
为了求的不同空间坐标系下的协方差的正负性，我们可以将坐标空间分为（1）、（2）、（3）、（4）四个区域

判断原始坐标空间中的协方差的正负性：

（1）区域中的有 X＞E[X]=0，Y＞E[Y]=0，所以(X-E[X])(Y-E[Y])=XY＞0

（2）区域中的有 X＜E[X]=0，Y＞E[Y]=0，所以(X-E[X])(Y-E[Y])=XY＜0

（3）区域中的有 X＜E[X]=0，Y＜E[Y]=0，所以(X-E[X])(Y-E[Y])=XY＞0

（4）区域中的有 X＞E[X]=0，Y＜E[Y]=0，所以(X-E[X])(Y-E[Y])=XY＜0

从面积上可以清楚的看出，区域（1）和（4）的面积远大于区域（2）和（3）的面积，所以Cov(X,Y)=E[(X-E[X])(Y-E[Y])]=E[XY]＞0的，因此，在原始坐标空间中，特征X和Y呈现正相关

判断新坐标空间中的协方差的正负性：

（1）区域中的有 X'＞E[X']=0，Y'＞E[Y']=0，所以(X'-E[X'])(Y'-E[Y'])=X'Y'＞0

（2）区域中的有 X'＜E[X']=0，Y'＞E[Y']=0，所以(X'-E[X'])(Y'-E[Y'])=X'Y'＜0

（3）区域中的有 X'＜E[X']=0，Y'＜E[Y']=0，所以(X'-E[X'])(Y'-E[Y'])=X'Y'＞0

（4）区域中的有 X'＞E[X']=0，Y'＜E[Y']=0，所以(X'-E[X'])(Y'-E[Y'])=X'Y'＜0

从面积上可以清楚的看出，区域（1）和（4）的面积等于区域（2）和（3）的面积，所以Cov(X',Y')=E[(X'-E[X'])(Y'-E[Y'])]=E[X'Y']=0的，因此，在新坐标空间中，特征X'和Y'不相关

由此，不难看出，通过对数据的线性变换，使数据在一个新的空间坐标系中进行表示，确实可以降低数据点不同特征之间的相关性，同时，看到上面的图片，是不是很眼熟，对，没错，跟PCA主成分分析中求出特征向量，然后把数据X映射到新的特征空间的做法一毛一样，那么我们也就可以知道，PCA主成分分析也可以降低数据点特征之间的相关性

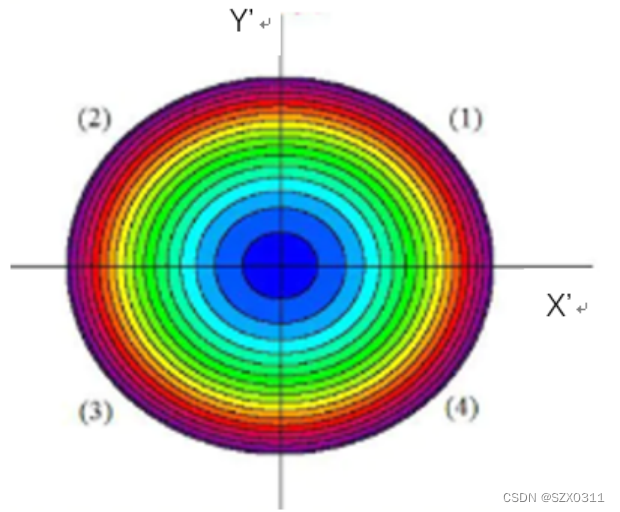
另外，我们将新坐标空间中的X'轴进行压缩，也就可以将数据点构成的云图变成一个圆，如下图所示，这也就是“数据白化”的另一个要求：所有的特征具有相同的方差。而这也就是为什么“数据白化”又叫做“球化”或者“圆化”的原因。

本文所有参考的文章链接如下：

机器学习（七）白化whitening_特征白化-CSDN博客

相关 (概率论)-数学百科 (shuxueji.com)

机器学习-特征中的相关性及相关系数、卡方检验、互信息_特征相关性-CSDN博客

协方差_百度百科 (baidu.com)