【基础】数据结构笔记1 复杂度分析

复杂度分析重要性

复杂度分析是整个算法学习的精髓，只要掌握了它，数据结构和算法的内容基本上就掌握了一半。¹
事后统计法的局限性：

1. 测试结果非常依赖测试环境
2. 测试结果受数据规模的影响很大

因此，需要一个不用具体的测试数据来测试，就可以粗略地估计算法的执行效率的方法。这就是时间、空间复杂度分析方法。

注：王争书里的代码有点点错误，本文已勘误。

大 O 复杂度表示方法

代码 1

// 求1,2,...,n的和
// 每行旁边的注释，表明该行的执行次数
int cal(int n) {
	int sum = 0;  // 1
	int i = 1;  // 1
	for (; i <= n; ++i) { // n
		sum = sum + i;  //n
	}
	return sum;
}

假定每行执行时间都一样，时间复杂度：
$f(n)=2+2n$
$T(n)=O(f(n))=O(n)$

代码 2

// 每行旁边的注释，表明该行的执行次数
int cal(int n) {
	int sum = 0; // 1
	int i = 1; // 1
	int j = 1; // 1
	for (; i <= n; ++i) { // n
		j = 1; // n
		for (; j <= n; ++j) { // n*n
		sum = sum + i * j; // n*n
		}
	}
	return sum;
}

时间复杂度：
$f(n)=2n^2+2n+3$
$T(n)=O(f(n))=O(n^2)$

时间复杂度分析

方法

1. 只关注执行次数最多的一段代码
2. 加法法则：总复杂度等于量级最大的那段代码的复杂度
   若 $T_1(n)=O(f(n))$，$T_2(n)=O(g(n))$，
   则 $T(n)=T_1(n)+T_2(n)=max(O(f(n)),O(g(n)))=O(max(f(n),g(n)))$
3. 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
   若 $T_1(n)=O(f(n))$，$T_2(n)=O(g(n))$，
   则 $T(n)=T_1(n)\ast T_2(n)=O(f(n))\ast O(g(n))=O(f(n)\ast g(n))$

要点

复杂度分析关键在于熟能生巧，不需要死记硬背。所以需要多看案例，多分析，做到无招胜有招。

代码 1：加法法则

加法法则：总复杂度等于量级最大的那段代码的复杂度

// 每行旁边的注释，表明该行的执行次数
int cal(int n) {
	int sum_1 = 0;
	int p = 1;
	for (; p < 100; ++p) {
		sum_1 = sum_1 + p;  //100
	}
	
	int sum_2 = 0;
	int q = 1;
	for (; q < n; ++q) {
		sum_2 = sum_2 + q;  //n
	}
	
	int sum_3 = 0;
	int i = 1;
	int j = 1;
	for (; i <= n; ++i) {
		j = 1;
		for (; j <= n; ++j) {
		sum_3 = sum_3 + i * j;  //n^2
		}
	}
	
	return sum_1 + sum_2 + sum_3;
}

时间复杂度：
$f(n)=n^2+n+100$
$T(n)=O(f(n))=O(n^2)$

代码 2：乘法法则

乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

// 每行旁边的注释，表明该行的执行次数
int cal(int n) {
	int ret = 0;
	int i = 1;
	for (; i < n; ++i) {
		ret = ret + f(i);  //（外层）n
	}
	return sum;
}
int f(int n) {
	int sum = 0;
	int i = 1;
	for (; i < n; ++i) {
		sum = sum + i; // （内层）n
	}
}

时间复杂度：
$f(n)=n^2$
$T(n)=O(f(n))=O(n^2)$

几种常见的时间复杂度分析

O (1)

只要不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是 O (1)。

// 每行旁边的注释，表明该行的执行次数
int i = 8; // 1
int j = 6; // 1
int sum = i + j; // 1

时间复杂度：
$f(n)=3$
$T(n)=O(f(n))=O(1)$

O (logn)，O (nlogn)

对数阶时间复杂度非常常见，也最难分析。

// 每行旁边的注释，表明该行的执行次数
int i = 1; // 1
while (i <= n) {
	i = i * 2; // 2^f(n)=n
}

时间复杂度：
$2^{f(n)}=n$，则 $f(n)={\log }_{2}n$
$T(n)=O(f(n))=O(\log n)$

将 2 改为 3，

// 每行旁边的注释，表明该行的执行次数
int i = 1; // 1
while (i <= n) {
	i = i * 3; // 3^f(n)=n
}

时间复杂度：
$3^{f(n)}=n$，则 $f(n)={\log }_{3}n$
$T(n)=O(f(n))=O(\log n)$

注意：${\log }_{3}n={\log }_{3}2\ast {\log }_{2}n$

O (m+n)，O (m * n)

代码的复杂度由两个数据的规模所决定。
加法法则失效，乘法法则不变。

// 每行旁边的注释，表明该行的执行次数
int cal(int m, int n) {
	int sum_1 = 0;
	int i = 1;
	for (; i < m; ++i) {
		sum_1 = sum_1 + i; // m
	}
	
	int sum_2 = 0;
	int j = 1;
	for (; j < m; ++j) {
		sum_2 = sum_2 + j; // n
	}
	return sum_1 + sum_2;
}

时间复杂度：
$f(n)=m+n$
$T(n)=O(f(n))=O(m+n)$

空间复杂度分析

渐近空间复杂度，表示算法的存储空间与数据规模之间的增长关系。

常见的空间复杂度是 $O(1)$，$O(n)$，$O(n^2)$，比较简单

代码示例

// 每行旁边的注释，表明该行申请的存储空间个数
void print (int n) {
	int i = 0; // 1
	int[] a = new int [n]; // n
	for (i; i < n; ++i) {
		a[i] = i * i;
	}

	for (i = n-1; i>= 0; --i) {
		print out a[i];
	}
}

空间复杂度：
$f(n)=n+1$
$S(n)=O(f(n))=O(n)$

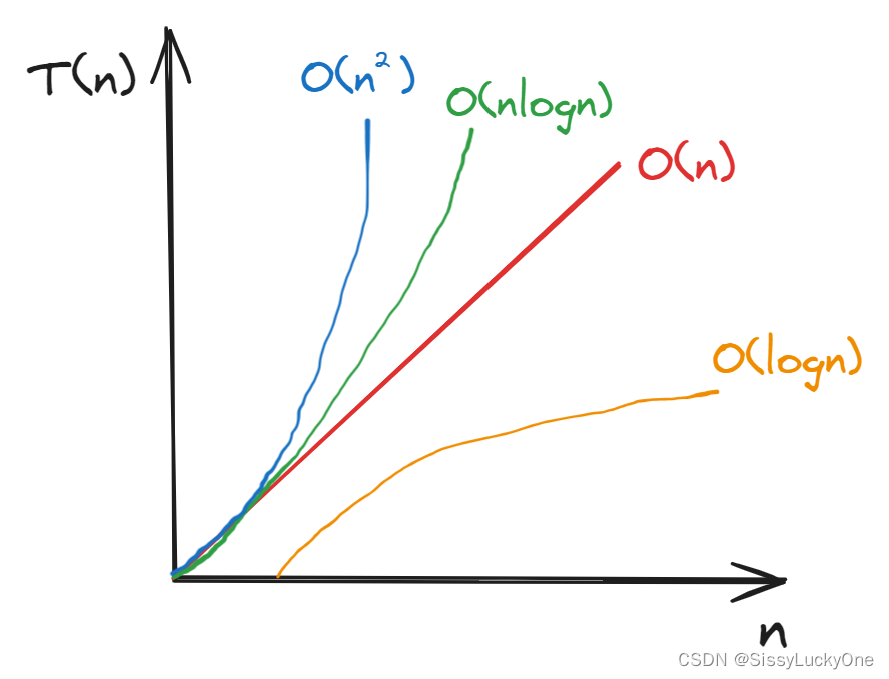
复杂度的阶数比较

$1<\log n<n<n\log n<n^2<2^n<n!<n^n$

最好、最坏情况时间复杂度

代码 1

// 实现功能：在一个长度为n的数组中，查找变量x出现的位置。找到返回位置，未找到返回-1
// n表示数组array的长度
// 每行旁边的注释，表明该行的执行次数
int find(int[] array, int n, int x) {
	int i = 0;
	int pos = -1;
	for (; i < n; ++i) {
		if (array[i] == x) pos = i; // n
	}
	return pos;
}

时间复杂度：
$f(n)=n$
$T(n)=O(f(n))=O(n)$

代码 2

将代码 1 优化，使得找到 x 位置时，提前结束循环。

// 实现功能：在一个长度为n的数组中，查找变量x出现的位置。找到返回位置，未找到返回-1
// n表示数组array的长度
// 每行旁边的注释，表明该行的执行次数
int find(int[] array, int n, int x) {
	int i = 0;
	int pos = -1;
	for (; i < n; ++i) {
		if (array[i] == x) {
			pos = i; // 1或2...或n
			break;
		}
	}
	return pos;
}

当 x 在数组中时，循环次数1 或 2… 或 n，因为退出后不再循环，但在什么时候退出，取决于 x 在数组中的位置是 0 或 1… 或 n-1。
当 x 不在数组中时，会循环 n 次而不会提前停止。

最好时间复杂度：
$f(n)=1$
$T(n)=O(f(n))=O(1)$

最坏时间复杂度 ：
$f(n)=n$
$T(n)=O(f(n))=O(n)$

平均时间复杂度

代码 1

// 实现功能：在一个长度为n的数组中，查找变量x出现的位置。找到返回位置，未找到返回-1
// n表示数组array的长度
// 每行旁边的注释，表明该行的执行次数
int find(int[] array, int n, int x) {
	int i = 0;
	int pos = -1;
	for (; i < n; ++i) {
		if (array[i] == x) {
			pos = i; // 1或2...或n
			break;
		}
	}
	return pos;
}

平均时间复杂度：

1. 假设每种情况出现的概率相同，则
   $f(n)=\frac{1+2+..+n+n}{n+1}=\frac{n(n+3)}{2(n+1)}$
   $T(n)=O(f(n))=O(n)$

2. 假设 x 在数组中的概率为 $\frac{1}{2}$，则
   $f(n)=1\times \frac{1}{2n}+2\times \frac{1}{2n}+...n\times \frac{1}{2n}+n\times \frac{1}{2}=\frac{3n+1}{4}$
   $T(n)=O(f(n))=O(n)$

---

1. 数据结构与算法之美，王争 ↩︎