单源点最短路Dijkstra算法及其优化

概念简介 

        Dijkstra算法由图灵奖获得者，荷兰计算机科学家Dijkstra于1959年提出的，主要利用贪心的思想来解决单源点最短路问题

        对于给定包含n个点的图的单源点最短路问题，Dijkstra算法的解决方案为：

        第一步：初始化。将所有点分为两个集合，源点到其最短路径已经确定的点集合S，源点到其最短路径未确定的点的集合T。初始时，源点s在集合中，即vis[s]=1；其余点都在集合T中，其余的vis[]的值为0；设置dis[s]=0，与源点s有边相连的点的dis[]值为s到其的边权，与源点s没有边相连的点的dis[]的值为正无穷。

        第二步：重复迭代n-1次，计算集合T中所有点的最短路dis[]值。每次迭代做两件事情：

                1、在集合T中，找最小dis[]的点y，确定点y的dis[]值为源点到y的最短路值，并将y加入到集合S中。

                2、利用刚加入的集合S的点y，对集合T中与y相邻的点做松弛操作。

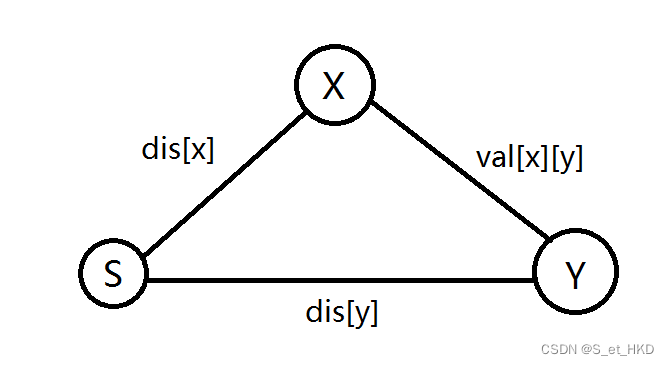
松弛操作：

 

如图：if(dis[x]+val[x][y]<dis[y]   dis[y]=dis[x]+val[x][y];

算法推导 

         我们可以通过下图推导Dijkstra算法

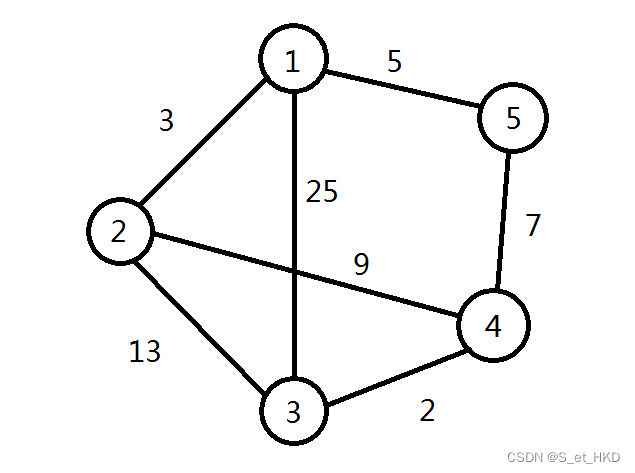
 初始阶段

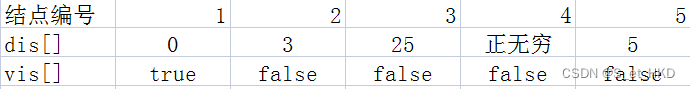
第一次迭代，找到最小的边权dis[2]=3，对T中的点进行松弛操作

第二次迭代，找到dis[5]=5，进行松弛操作

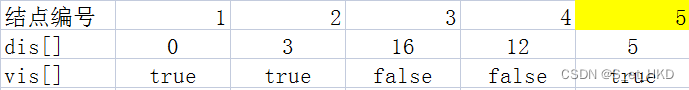
 第三次迭代，找到dis[4]=12，进行松弛操作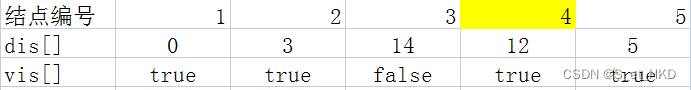

 第四次迭代，只剩下3号点，表格并未变化，问题解决。

---

 核心代码实现

根据上面的算法描述，我们可以得到Dijkstra算法的代码：

（邻接表版本）

void Dijkstra(int s)
{
	for(int i=1;i<=n;i++)	dis[i]=1e9;//dis[]初始化
	dis[s]=0;//起点赋值 
	vis[s]=1; 
	for(int i=Link[s];i;i=Edge[i].nxt) dis[Edge[i].y]=Edge[i].v;
	for(int i=1;i<n;i++)
	{
		int minn=1e9,u=0;
		for(int j=1;j<=n;j++)//寻找集合T中的dis[]最小值 
			if(!vis[j]&&dis[j]<minn)
				minn=dis[j],u=j;
		vis[u]=1;//将结点u放入S集合
		for(int j=Link[u];j;j=Edge[j].nxt)
		{
			int v=Edge[j].y;
			if(!vis[v]&&dis[v]>dis[u]+Edge[j].v)
				dis[v]=dis[u]+Edge[j].v;	
		} 
	}
}

Dijkstra算法的效率主要体现在第二步n-1次迭代时所消耗的时间

每次迭代寻找最小值的时间复杂度为O（），做松弛操作花费的总时间为O（|E|）,所以上述代码的时间复杂度为O（max（，|E|））

因此，我们要尽可能优化每次寻找最小值的操作 

每次方便地取出最小值，我们就能想到运用优先队列来优化每次迭代寻找最小值

代码如下（邻接表版本）：

struct node
{
	int pla,distant;
};
priority_queue<node> que;
bool operator < (node x,node y)
{
	return x.distant>y.distant;
}
void Dijkstra()
{
	dis[1]=0;
	que.push((node){1,0});//第一个点的下标，距离
	while(!que.empty())
	{
		int pp=que.top().pla;
		que.pop();
		if(vis[pp]) continue;
		vis[pp]=1;
		for(int i=Link[pp];i;i=Edge[i].cnt)
		{
			int qq=Edge[i].y;
			if(dis[qq]>dis[pp]+Edge[i].v)
			{
				dis[qq]=dis[pp]+Edge[i].v;
				que.push((node){qq,dis[qq]});
			}	
		}
	 } 
}

运用二叉堆（优先队列）可以轻松地找到迭代后的最小值，大大优化了算法的复杂度

---

---

---

例题

最短路计数

题目描述

给出一个 N 个顶点 M 条边的无向无权图，顶点编号为 1—N。

问从顶点 1 开始，到其他每个点的最短路有几条。

输入格式

第一行包含 2 个正整数 N,M，为图的顶点数与边数。

接下来 M行，每行两个正整数 x,y，表示有一条顶点 x 连向顶点 y 的边，请注意可能有自环与重边。

输出格式

输出 N 行，每行一个非负整数，第 i 行输出从顶点 1 到顶点 i 有多少条不同的最短路，

由于答案有可能会很大，你只需要输出 %100003 后的结果即可。如果无法到达顶点 i 则输出 0。

样例数据

input

5 7
1 2
1 3
2 4
3 4
2 3
4 5
4 5

output

1
1
1
2
4

数据规模与约定

对于 20 的数据，N100；

对于 60 的数据，N1000；

对于 100 的数据，1N100000,0M200000。

时间限制：1texts

空间限制：256textMB

 如果用邻接表（即链式前向星）或邻接矩阵来写，因时间复杂度为O（），所以要跑1e10，明显会超时，所以运用优先队列寻找最短路

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5*2+10;
struct fun
{
	int y,cnt;
}edge[maxn];
int link[maxn];
int len;
bool vis[maxn];
int dis[maxn];
int n,m;
int ans[maxn];
void insert(int x,int y)
{
	edge[++len].cnt=link[x];
	link[x]=len;
	edge[len].y=y;
}
void init()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int a,b;
		cin>>a>>b;
		insert(a,b);
		insert(b,a);
	}	
}
struct node
{
	int pla,distant;
};
priority_queue<node> que;
bool operator < (node x,node y)
{
	return x.distant>y.distant;
}
void Dijkstra()
{
	dis[1]=0;ans[1]=1;
	que.push((node){1,0});//第一个点的下标，距离
	while(!que.empty())
	{
		int pp=que.top().pla;
		que.pop();
		if(vis[pp]) continue;
		vis[pp]=1;
		for(int i=link[pp];i;i=edge[i].cnt)
		{
			int qq=edge[i].y;
			if(dis[qq]>dis[pp]+1)
			{
				dis[qq]=dis[pp]+1;
				que.push((node){qq,dis[qq]});
			}	
			if(dis[qq]==dis[pp]+1)
				ans[qq]=(ans[qq]+ans[pp])%100003;
		}
	 } 
}
int main()
{
	init();
	memset(ans,0,sizeof(ans));
	memset(dis,10,sizeof(dis));
	Dijkstra();
	int num[maxn];
	for(int i=1;i<=n;i++)
		cout<<ans[i]<<endl;
}