基于Excel的QR二维码生成工具——原理及算法详解（之二）

在前一篇文章中，我们探索了在Excel中通过一组工作表函数计算出了伽罗华域$GF(2^8)$的全部元素：

$$\{1,2,4,\ldots,142\}$$ ,但是这只是RS纠错码计算的第一步基础工作。接下来，我们还需要研究如何构建“生成多项式 $g(x)$”，并且探索如何在Excel中实现多项式的求余以便实现RS纠错码的计算。

RS码通常可以表示为$RS(n,k)$的形式，$n$和$k$都是正整数且$n>k$。其中$n$表示数据码加上纠错码的长度，而$k$表示数据码的长度，$n-k$为纠错码的长度。一般来说，所谓的数据码就是一串由正整数组成的一维数组，数组中的每一个元素的取值都必须在伽罗华域的元素集合内。由于一个字节取值正好在0~255之间，正好可以与$GF(2^8)$的元素一一对应，这就是为什么在计算机领域$GF(2^8)$的应用最为广泛的缘故之一。因此，在计算QR的RS纠错码时，所有的数据一定都是通过某种规则首先编成一组0~255之间的整数数组的，而且这个数组中元素的数量一定等于$k$，这样通过计算后能得到另外一个数组，其元素同样是0~255之间的整数，且数量为$n-k$，这个数组就是纠错码。将两个数组连接在一起，数据码在前，纠错码在后，连接成一个长度为$n$的数组，就形成了完整的RS纠错编码。

为了完成上述计算，通常将所有的数组都写成多项式的形式，其中每一项的系数就是编码各位置上的元素，比如，要计算以下数据码的$RS(9,3)$码：
其中，$n=9, k=3$，因此数据码有三个码字：
数据码：

$$\{123,76,91\}$$ 而生成的完整RS码应该有9个码字： $$\{123,76,91,EC_0,EC_1,EC_2,EC_3,EC_4,EC_5\}$$ 其中 $EC_i (0<i<5)$表示纠错码的六个码字。为了完成上述计算，我们应该首先将数据码字写成多项式的形式： $$123x^2+76x^1+91x^0$$ 而为了使计算完成的纠错码有九个元素，在计算之前先将多项式乘以 $x^6$以便获得足够的幂次： $$x^6(123x^2+76x^1+91x^0)=123x^8+76x^7+91x^6$$ 接下来，使用这个多项式对所谓的“生成多项式 $g(x)”求余。关于生成多项式的构件下文还会详细解释，这里我们只需要知道针对每一个不同的$n-k $其生成多项式的计算公式为：$ $$g(x)=(x+a)(x+a^2)(x+a^3)\cdots(x+a^{n-k})$$ 其中 $a$就是$GF(2^8)$上的“本原元”而且使用伽罗华域的运算法则（参见上一篇文章）。 $g(x)$在Excel中的生成算法后文再讨论，这里先直接给出 $(n-k)=6$的生成多项式如下： $$g(x)=1x^6+126x^5+4x^4+158x^3+58x^2+49x+117$$ 用 $GF(2^8)$的本原元 $a$的幂次表示则是： $$g(x)=a^0x^6+a^{167}x^5+a^2x^4+a^{137}x^3+a^9x^2+a^{181}x+a^{21}$$ 因为我们知道伽罗华域上的元素都可以表示为 $a^n$的形式，因此上面两个式子完全是等价的

接下来，只要将数据码多项式对生成多项式求余，就可以得到EC多项式了:

$$EC = (123x^8+76x^7+91x^6) \ mod \ g(x) \\ = 199x^5+42x^4+174x^3+181x^2+134x+95$$
从上面的理论计算过程可以发现，在Excel中实现的难点有两个：

1. 实现多项式的求余，并且要采用伽罗华域的运算法则
2. 计算生成多项式

上面两个问题都可以通过工作表函数来实现，当然，VBA也没问题，下面先探讨工作表函数的方法。
首先需要解决伽罗华域上的加法和乘法的问题，伽罗华域上的加法其实是Xor运算，Excel的工作表并没有给出异或运算的函数，因此我的解决办法是自己写一个工作表函数CALCXOR(n1,n2)用于计算异或：

Private Function calcXor(n1 as long, n2 as long)as long
    calcXor = n1 Xor n2
End Function

而乘法运算的定义是两个元素的本原元幂次相加，因此计算乘法需要两步，首先找出两个本原元的幂次，相加后再找到新的元素值，如：在$GF(2^8)$上计算123*126的结果，需要将123*126表示为

$$a^{172}*a^{126} = a ^{172+126} = a^ {298\ mod\ 255} = a^{43} = 32$$ 在Excel中我简单地做了一张对照表，并使用Vlookup函数查找元素对应的幂次，同时查找幂次对应的元素，这样就可以一步完成乘法计算：

接下来，就需要完成多项式的求余，如果我们将多项式的系数写在表格中，那么前面的例子可以列表如下：

N	$x^8$	$x^7$	$x^6$	$x^5$	$x^4$	$x^3$	$x^2$	$x^1$	$x^0$
除数$g(x)$	1	126	4	158	58	49	117
被除数（数据码）	123	76	91	0	0	0	0	0	0
商1：$123*g(x)$	123	32	82	97	94	230	3
余数1（数据Xor商1）	0	108	9	97	94	230	3
商2：$108*g(x)$	0	108	187	72	168	82	11	136
余数2（余数1Xor商2）	0	0	178	41	246	180	8	136
商3：$178*g(x)$	0	0	178	238	220	26	189	14	95
余数3（余数2Xor商3）	0	0	0	199	42	174	181	134	95

于是，根据上表最终计算出余数，就是数据码的纠错码多项式，因此完整的纠错码多项式为：

$$\{123,76,91,199,42,174,181,134,95\}$$
在Excel中我使用了一系列的工作表函数填充到类似上表的单元格中，完成了计算纠错码的任务：
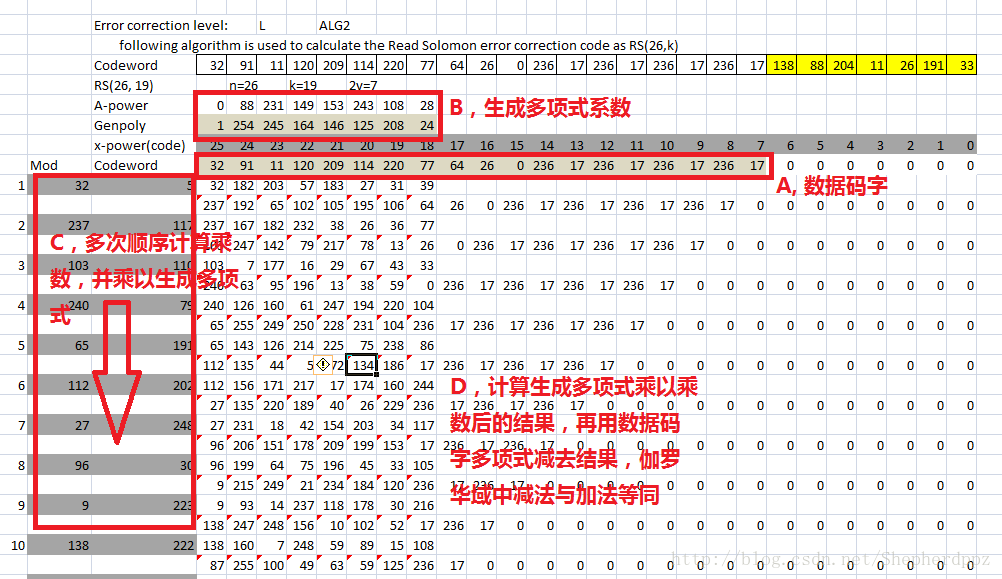上图中，Codeword后的那一列是数据码的输入，黄色底纹的单元格则是计算结果。图中可以看到计算的是RS(26,19)，也就是说19个输入码字，输出7个纠错码字。一般来说，使用这样的工作表函数阵列，只需要重复乘数* $g(x)$，再用上一次的计算结果Xor乘积就可以了，跟笔算除法的规则非常类似，并且重复 $k$次，就得到正确的纠错码了

在这篇文章里，我们讨论了使用工作表函数计算RS纠错码，下一篇文章里，我们再来看如何计算生成多项式$g(x)$，并且讨论使用VBA计算RS纠错码