gcd和ex_gcd

1.

• gcd  最大公约数（欧几里得）

• ex_gcd 扩展欧几里得：就是 gcd 的逆过程

2.

% 求余符号,a%b=r,a=kb+r

| 整除符号,a|b,表示a能整除b,即b=ka,b%a=0

≡≡ 同余符号,a≡𝑏(𝑚𝑜𝑑 𝑐)a≡b(mod c) 为一个同余式，表示a%c=b%c

3.

对于辗转相除法的实现，我们有递归和非递归两种方式

1.非递归

int gcd(int a,int b){
int r;
    while (b){
        r=a%b;
        a=b;
        b=r;
    }
    return a;
}

 2.递归

int gcd(int a,int b){
    return b?gcd(b,a%b):a;
}

3.lcm

当然我们求最小公倍数也是通过先求最大公约数得到的。a和b的最小公倍数表示为：

lcm(a,b)。

在这里有一个很重要的结论：

 

4.素因子求gcd

 当然，求最大公约数和最小公倍数还有另外一种方法：就是素因子分解。

p对于a和b，求它们的最大公约数，那么先把a和b素因子分解：

a和b的最大公约数就可以这样计算

最小公倍数就是取最大值

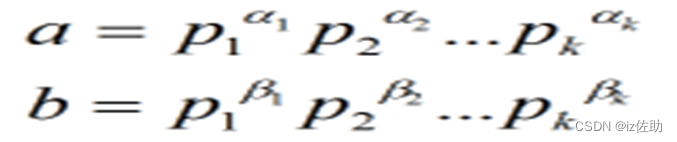
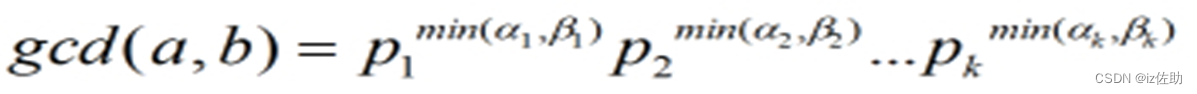
5.

在有些题目中涉及多个数的最大公约数和最小公倍数。

对于这种问题，基本思想就是两两合并。例如求n个数的最大公约数，就可以这样

int work(int a[],int n){
    int s=a[0];
    for(int i=1;i<n;i++){
        s=gcd(s,a[i]);
    }
    return s;
}

 6.拓展gcd和逆元

扩展欧几里得算法：用来求 ax+by=t 方程的整数解。其中， t=gcd(a,b) 。

• 当 b=0 时 a是 两个整数的 gcd，一对整数x=1,y=0使得 ：

   a×1 + 0×0 = gcd(a,0)

  成立。

• 当 b 不等于 0 时， gcd(a,b)=gcd(b,a%b)

• 这里的 a%b=a-b*(a/b)

• b*x1+(a%b)*y1

• =b*x1 + (a-b*(a/b))*y1

  = b*x1 + a*y1-b*(a/b)*y1

  = a*y1 + b(x1-(a/b)*y1

• x=y1,y=x1-(a/b)*y1

代码实现：

方法一：

void ex_gcd(int a,int b,int &x,int &y){
    if(b==0){
        x=1;
        y=0;
        return;
    }
    int x1,y1;
    ex_gcd(b,a%b,x1,y1);
    x=y1;
    y=x1-(a/b)*y1;
}

方法二：

void Ex_gcd(int a,int b,int &x,int &y){
    if(b==0){
        x=1;
        y=0;
        return;
    }
    ex_gcd(b,a%b,x,y);
    int t=x;
    x=y;
    y=t-(a%b)*y;
}

以上两个都可以，但本人推荐第二种。

1.什么是逆元？

• 如果 𝒂𝒙 ≡ 𝟏 ( 𝒎𝒐𝒅  𝒃 ) ax≡1(mod b) ，则称 x 为 a 在 模 b 下 的逆元，可以记作： 𝒂 − 𝟏 a^(-1) 。

• 如果 a 和 b 互素 ，即 gcd ( a,b ) = 1 时， ax+by =1

• ax≡1 （ mod b)

例如：

18x+7y=1方程的特解为：x=2,y=-5；

18x ≡≡ 1 (mod 7) 的特解为2

7x+18y=1方程的特解为：x=-5,y=2；

7x ≡≡ 1 (mod 18) 的特解为-5

2. 逆元有什么用？

  在处理𝑎𝑏%𝑐a/b%c时，取模运算对除法是没有分配律的，因为先取模不能保证余数能整除。

360/18%7的结果应该是20%7，即6，如果先取模，360%7=3，18%7=4，余数不能整除360/18%7的结果应该是20%7，即6，如果先取模，360%7=3，18%7=4，余数不能整除

可以先求出b在模7下的逆元𝑏−1b^(-1)，这样 𝑎𝑏≡ 𝒂 𝒃−𝟏(𝒎𝒐𝒅 𝒎)a/b≡ a b^(-1) (mod m)就可以把原来除法的取模运算转化成乘法的取模运算

求解360/18%7时应该先求解18的逆元18−1，即18𝑥≡𝟏（𝒎𝒐𝒅𝟕），然后计算360∗𝑥%7求解 360/18%7时应该先求解18的逆元18^(-1)，即18x≡1（mod7），然后计算360∗x%7

求解思路

• 将 𝟏𝟖 𝒙 ≡ 𝟏 ( 𝒎𝒐𝒅  𝟕 )18x≡1(mod 7) 转化为求方程 18x+7y=1 方程 x 的整数解， 即 18 的逆元 2 。即18的逆元2。

• 将 18 的逆元代入，（ 360%7 *(2%7) ） %7 ，即 3*2%7=6 ，即求出正确结果

• 注意，这里逆元应该是正整数，要求解方程 x 的最小正整数解

• 利用 ex_gcd 求解的 7 在模 18 下的逆元却为 -5

计算出的x是负数的话，要变成正数：

 if(x<0){
        x=(x+b)%1007;
    }

7.例题：

F(n)=(1/6*n*(n+1)*(2n+1))%1007 取余

1/6 如何处理？

6x+1007y=1 等价 6x≡1(mod 1007)

题解：

//
// Created by w1897 on 2024/3/27.
//
#include <iostream>

using namespace std;
void  E_gcd(long long a,long long  b,long long &x,long long &y){
    if(b==0){
        x=1;
        y=0;
        return;
    }
    E_gcd(b,a%b,x,y);
    long long  temp=x;
    x=y;
    y=temp-(a/b)*y;
}

int main(){
    long long n,x,y;
    E_gcd(6,1007,x,y);
    if(x<0){
        x=(x+1007)%1007;
    }
    while (cin>>n){
        long long q=n%1007;
        q=q*(n+1)%1007;
        q=q*(2*n+1)%1007;
        q=(q*x)%1007;
        cout<<q<<endl;
    }

    return 0;
}