多路径问题的几种解决方法

多路径

【问题描述】

       给定一个有向图 G ，可以包含环，也可以有自环（节点连接到自身）,一对顶点之间最多有一条边相连。顶点编号从1~n 。

       从顶点 u 到 v 的路径是一个边的序列，描述如下

• • 顶点 u 是路径上第一条边的开始顶点

  • 顶点 v 是路径上最后一条边的结束顶点

  • 对于所有相邻边对，后一条边的开始顶点是前一条边的结束顶点

       假定边的空序列是从 u 到 u 的路径。

       对于每个顶点 v ，输出以下四个值之一：

• • 0，表示从顶点 1 到 v 没有路径

  • 1，表示从顶点 1 到 v 只有一条路径

  • 2，表示从顶点 1 到 v 有超过一条路径，且路径数是有限的

  • -1，表示从顶点 1 到 v 有无穷多条路径

 那么

• • 顶点1的结果为1：从1到1只有一条路径（路径长度为0）

  • 顶点2的结果为0：从1到2没有路径

  • 顶点3的结果为1：从1到3仅有一条路径（为边（1,3））

  • 顶点4的结果为2：从1到4有超过一条路径，但路径数量是有限的（两条路径：【（1,3），（3,4）】和【（1,4）】）

  • 顶点5的结果为-1：从1到5的路径数是无穷的（环可以用于路径无穷多次）

  • 顶点6的结果为-1：从1到6的路径数是无穷的（环可以用于路径无穷多次）

 

【输入形式】

 

       输入的第一行为一个整数 t （1≤ t ≤104），表示测试用例的组数，接下来是 t 个测试用例，每个测试用例前有一个空行，这个空行的作用仅为阅读方便，有否不影响最终结果。

 

      每个测试用例的第一行为两个整数 n 和 m (1≤ n ≤ 4×105，1≤ m ≤ 4×105)，分别表示图的顶点数和边数。接下来的 m 行包括了对边的描述，每行两个整数 ai、bi (1≤ ai、bi  ≤ n)，表示第 i 边的开始点和结束点，图的顶点编号从1至 n ，给定的图中可以包含环（可能有ai =bi）, 但不可以包含多边（即对于 i ≠ j，不可能有 ai = aj 以及 bi = bj）。

 

       所有测试用例中 n 之和不超过4×104，同样的，所有的 m 之和不超过4×104。

 

【输出形式】

         输出包括 t 行，第 i 行是第 i 个测试用例的答案，为一个 n 个整数序列，取值在-1到2之间。

【样例输入】

5

6 7
1 4
1 3
3 4
4 5
2 1
5 5
5 6

1 0

3 3
1 2
2 3
3 1

5 0

4 4
1 2
2 3
1 4
4 3

【样例输出】

1 0 1 2 -1 -1 
1 
-1 -1 -1 
1 0 0 0 0 
1 1 2 1

Problem - 1547G - Codeforces

一、问题分析

分析并确定要处理的对象（数据）是什么

要处理一片图

分析并确定要实现的功能是什么

求解从节点1到每一个节点的连通性。不连通0单连通1连通2强连通-1

分析并确定处理后的结果如何显示

将每个节点对应的连通性存入一个vector中，遍历输出即可

请用题目中样例，详细给出样例求解过程。

这里给出多种解决方法

双DFS，Tarjin算法

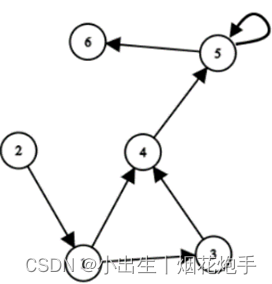
对于样例

输入为

6 7

2 1

1 4

1 3

3 4

4 5

5 5

5 6

我们使用邻接表存图，顺便存储一下每一个点的入度。

 

双DFS

之后从节点1开始进行第一次DFS，这一步我们可以求出节点1的极大连通子图（找到了就先改变它的状态为1），并且求出在每个环中的某一个元素。

这里为什么可以求出来每个环中的某一个元素呢？其实我们的第一遍DFS主要是判断成不成环，为什么DFS能判断是否成环呢？我们都知道DFS实际上是一条路走到死，然后再回溯找到之前的那个没有走完的分支节点继续走。这利用了栈的先进后出LIFO的特性来实现的，那么，如果一条路走到它自己了，那不就证明有环了嘛。

接下来，对找到的那些环里面的元素全部加到向量里面，再对以每个元素为起点，进行DFS，他们访问过的所有节点全是连通的（改变它的状态为-1）。

剩下的步骤就好办了，我们已经得到所有节点1的极大连通子图和所有成环的节点了，接下来遍历这个极大连通子图，如果这个子节点的状态不是-1（成环），并且入度大于等于2，那么它就是连通的了。

这样子状态0，-1，1，2都找齐了。

#include<iostream>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;

static const int bn=400;

void dfs(int a,vector<vector<int>>& graph,vector<int>& visit,vector<int>& cyc){
	//如果是一个有向无环图，必然有一个节点啥都没有链接，自己就退出了;
	visit[a]=1;
	//cout<<a<<" visited"<<endl;
	for(auto i:graph[a]){
		if(visit[i]==1){
			cyc[i]=1;
			
		}else if(visit[i]==0){
			dfs(i,graph,visit,cyc);
		}
	}
	visit[a]=2;
}
int solve() {
	int n,m;//vertex,edge
	cin>>n>>m;
	if(n==0){
		cout<<endl;
		return 0;
	}
	if(n>=0&&m==0){
		cout<<1<<' ';
		for(int i=2;i<=n;i++){
			cout<<0<<' ';
		}
		cout<<endl;
		return 0;
	}
	vector<int> visit(n+1,0);
	vector<vector<int>> graph(n+1,vector<int>(0,0));
	vector<int> reach1(n+1,1);
	vector<int> count(n+1,0);
	vector<int> inCycle(n+1,0);
	for(int i=1;i<=m;i++){
		int t1,t2;
		cin>>t1>>t2;
		graph[t1].push_back(t2);
		count[t2]++;
	}
	dfs(1,graph,visit,inCycle);
	for(int i=1;i<=n;i++){
		if(visit[i]==0){
			
			reach1[i]=0;
		}
	}
	vector<int> visit2(n+1,0);
	for(int i=1;i<=n;i++){
		if(visit[i]>0&&inCycle[i]==1){
			dfs(i,graph,visit2,inCycle);
		}
	}
	for(int i=1;i<=n;i++){
		if(visit2[i]>0){
			inCycle[i]=1;//cout<<i<<"in cycle"<<endl;
			reach1[i]=-1;
		}
	}
	for(int i=1;i<=n;i++){
		for(auto p:graph[i]){
			if(inCycle[p]&&visit[p]==2){
				reach1[p]=-1;
			}
			else if(count[p]>=2&&visit[p]==2){
				reach1[p]=2;
			}
		}
	}
	for(int i=1;i<=n;i++){
		cout<<reach1[i]<<' ';
	}
	cout<<endl;
	return 0;
}
int main(){
	int t;
	cin>>t;
	while(t--){
		solve();
	}
}

 

接下来是一些成熟算法。

Tarjin算法

Tarjin算法本质就是在一次DFS中维护了一个dfn（遍历的时间戳）和一个low表示按照low这个方向进行访问，能够访问到的最早的节点的时间戳。这个算法通过一个栈和一个记录节点是否在栈中的一个数组来维护dfn和low

v未被访问：继续对v进行深度搜索。在回溯过程中，用 low[v]更新low[u]。因为存在从u 到 v的直接路径，所以v能够回溯到的已经在栈中的结点，u 也一定能够回溯到。

v被访问过，已经在栈中：根据low值的定义，用dfn[v]更新low[u]。

v被访问过，已不在栈中：说明v已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。

它的优点在于最大化利用了DFS的回溯特性，只用了一次DFS就把强连通的点找出来了，这里只用找到第一片强连通分量以后就可以把剩下点的状态全部变为-1了。

之后的问题已经宛如风中残烛，遍历全图就可以把剩下1，2，0状态的点找齐，岂不美哉。

还有Kosaraju算法，这里不多作介绍了。

二、数据结构和算法设计

抽象数据类型设计

邻接表graph vector<vector<int>> graph(n+1,vector<int>(0,0));

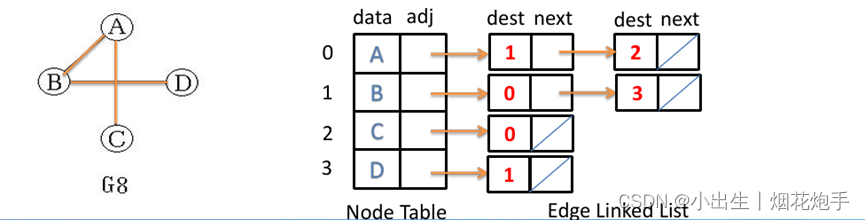
物理数据对象设计（不用给出基本操作的实现）

       vector<int> visit(n+1,0);记录第一次访问过的节点（节点1的极大连通子图）

       vector<int> reach1(n+1,1);记录每个点的状态

       vector<int> count(n+1,0);记录每个点的入度

       vector<int> inCycle(n+1,0);记录每个点是否在环中

vector<int> visit2(n+1,0);记录每个环中点所在的极大连通子图

算法思想的设计

大部分思想已经在前面的样例解析中给出，这里做一次总结。

DFS遍历全图的思想：这样可以得到一片极大连通子图

判断成环算法的思想：利用了栈的先进后出特性，如果重复入栈，那就说明这个点是在环中的

关键功能的算法步骤

1. 每次在输入边的时候直接让后继节点的度数加一，减少遍历次数;
2. DFS，通过递归来遍历全图，这里设置访问过有两个状态是为了判断一个点是否被重复访问，如果那个点对应的值变为2，那就是访问完了，不需要再考虑这个节点了，这也是为了防止重复地访问每个节点。
3. 对在环中的每个节点DFS，它们的极大连通子图中的点都可以被认为是由无数条可达路径的。

 

三、算法性能分析

本人使用的是双DFS算法，一次DFS的时间代价为O(V+E)，设有m个环，接下来还要进行m次DFS，因此时间复杂度为O(m(V+E))，由渐进分析法可知后面遍历全图的时间复杂度可以忽略不计，因此双DFS的时间复杂度是O(m(V+E))

Tarjin算法的时间复杂度是O(V+E)，因为只用进行一次DFS。