粒子系统于 1983 年由 reeves 提出 ,最初它并不是针对非刚性物体的建模而提出,它是为了解决对一些自然现象和自然景物的模拟而产生的,如雨,雪,雾,水波,火焰,焰火,烟尘,流星等自然现象,后来才逐渐的用于对非刚性的物体建模之中。
构成物体的物质都是由基本粒子构成,水由水 分子构成,烟雾由气体分子和尘埃构成,火焰由光子和空气微粒构成,研究这些构成物质的粒子的状态和运动方式,并建立相应的物理模型,就可以用计算机模拟出 相应的自然现象。粒子系统的方法就是将大量的粒子单元集合在一起,通过其属性的变化表现物体的物理特性的物体模拟方法。每个粒子是有着形状大小颜色透明度 位置及速度等属性的几何单元,一个粒子究竟有什么样的属性主要取决于具体的应用。粒子系统不是一个简单的静态系统,随着时间的推移,系统中已有的粒子不仅 不断改变形状,不断运动,而且不断有新的粒子加入,并有旧粒子的消失,这样才能演示出我们这个变幻万千,生机勃勃的世界。而粒子与我们显示设备中的像素具 有一定的相通相似性。利用一个或者多个像素构造粒子,再赋予粒子各种属性,状态,运行轨迹,把成百上千个同样的粒子组合起来,利用随机函数,程序员有时可 以创造出令艺术家都惊叹的视觉效果。
最近在网上阅读突然对粒子起了兴趣,趁空闲时研究了一下网上有关粒子编程的水波,火焰,下雪效果,按照相应的算法,写出相应的手机算法,初期效果不理想,后期根据相应手机平台优化后,运行速度得到极大提升,在某些情况下,我不得不使用 TIMER 延缓每帧播放的速度。
三种效果,水波的模拟运算量最高,火焰次之,下雪最少。下雪特效使用了网上通用的算法,几乎不做优化就能使用。我做的工作主要在于单个雪花形状的渲染,通过设计不同形状,不同大小,不同水平升垂直速度的雪花,体现某种空间感。使用 FOR 循环随机为雪花赋值坐标,橫向速度,纵向速度,生命周期,不同大小的雪花可以形成空间层 次感,速度的不同可以表现出雪花随风的动态,雪花生命周期结束时停留下来生成雪地。这个程序也可以模拟落叶和落花效果和下雨效果,就是更改一下横向的速 度,落叶和落花由于空气浮力的存在,在下落上会表现的更大的横向飘移,雨的纵向速度要比横向更大一些,而且偏移方向更一致一些。效果如下,左边是原图,右 边是加入了飞落雪花的效果。


雪花渲染如下:
void drawonwsnow(S32 x, S32 y, gdi_color c)
{
switch (rand()%16)
{
case 0:
gdi_act_put_pixel(x, y, c);
break;
case 1:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
break;
case 2:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(y-1, y, c);
break;
case 3:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
break;
case 4:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
break;
case 5:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
break;
case 6:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
break;
case 7:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y-1, c);
break;
case 8:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y+1, c);
break;
case 9:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
break;
case 10:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
gdi_act_put_pixel(x-1, y-1, c);
gdi_act_put_pixel(x+1, y+1, c);
gdi_act_put_pixel(x+1, y-1, c);
gdi_act_put_pixel(x-1, y+1, c);
break;
case 11:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
gdi_act_put_pixel(x-1, y-1, c);
gdi_act_put_pixel(x+1, y+1, c);
gdi_act_put_pixel(x+1, y-1, c);
gdi_act_put_pixel(x-1, y+1, c);
gdi_act_put_pixel(x-2, y, c);
break;
case 12:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
gdi_act_put_pixel(x-1, y-1, c);
gdi_act_put_pixel(x+1, y+1, c);
gdi_act_put_pixel(x+1, y-1, c);
gdi_act_put_pixel(x-1, y+1, c);
gdi_act_put_pixel(x+2, y, c);
break;
case 13:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
gdi_act_put_pixel(x-1, y-1, c);
gdi_act_put_pixel(x+1, y+1, c);
gdi_act_put_pixel(x+1, y-1, c);
gdi_act_put_pixel(x-1, y+1, c);
gdi_act_put_pixel(x, y-2, c);
break;
case 14:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
gdi_act_put_pixel(x-1, y-1, c);
gdi_act_put_pixel(x+1, y+1, c);
gdi_act_put_pixel(x+1, y-1, c);
gdi_act_put_pixel(x-1, y+1, c);
gdi_act_put_pixel(x, y+2, c);
break;
case 15:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
gdi_act_put_pixel(x-1, y-1, c);
gdi_act_put_pixel(x+1, y+1, c);
gdi_act_put_pixel(x+1, y-1, c);
gdi_act_put_pixel(x-1, y+1, c);
gdi_act_put_pixel(x, y+2, c);
gdi_act_put_pixel(x, y-2, c);
gdi_act_put_pixel(x+2, y, c);
gdi_act_put_pixel(x-2, y, c);
break;
default:
gdi_act_put_pixel(x, y, c);
gdi_act_put_pixel(x-1, y, c);
gdi_act_put_pixel(x+1, y, c);
gdi_act_put_pixel(x, y-1, c);
gdi_act_put_pixel(x, y+1, c);
break;
}
}
而对于火焰来说,就没有那么幸运,每一帧差不多要对一个完整的屏幕大小的数据 BUFFER 运算赋值,这使得他的渲染不能再使用 gdi_act_put_pixel 直接赋值,需要直接修改单个屏幕层的 BUFFER 来实现。火焰算法网上有很多,这里不多讲解:
1. 放置火源
for(x=0;x<blue_w-1;x++)
{
//srand(time(NULL));
fire[blue_h-1][x]=rand()%256;
}
2 .火焰上升,原本要除以四,考虑到火焰衰减,这里从乘以 1000 ,除以 3925 得到,主要用于优化速度,避免除以一个浮点数降低程序的效率。
fire[y][x]=(S32)(((fire[y][x]+fire[y+1][x-1]+fire[y+1][x+1]+fire[y+1][x])*1000)/3925)%256;

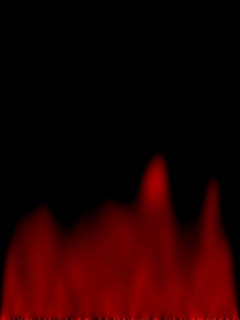
左边是小火,右边是加入了衰减后的大火,可以渲染整个窗口
对于水波算法,网上也有很多,主要是考虑到折射和衰减,其运算量大约相当于三到四屏次数的运算,为了优化算法,达到每秒十帧到二十帧。算法的优化是必不可少的,最重要的还是渲染,水波详细算法可以在网上看到,首先和火焰一样,放置波源:
1 .放置波源
// 加入波源
void DropStone(S32 x,S32 y, U16 stonesize, U8 stoneweight)
{
S32 posx, posy;
if ((x + stonesize) > MY_WATER_W || (y+stonesize) > MY_WATER_H ||
(x-stonesize)<0 ||(y-stonesize)<0)
{
return;
}
for (posx = x - stonesize; posx < x+stonesize; posx++)
{
for (posy = y-stonesize; posy < y+stonesize; posy++)
{
if ((posx-x)*(posx-x) + (posy-y)*(posy-y) < stonesize*stonesize)
{
my_water_buf1[MY_WATER_W*posy+posx] = -stoneweight;
}
}
}
}
2 .计算缓冲区,这段代码出于效率考虑,我对他做了优化,比网上的多了一些代码,细心的朋友很快就能发现
// 计算缓冲区
void RippleSpread()
{
S32 i, j;
char * p;
if (isrun)
{
for (i=MY_WATER_W; i<MY_WATER_W*MY_WATER_H-MY_WATER_W; i++)
{
// 波能扩散
my_water_buf2[i] = ((my_water_buf1[i-1]+
my_water_buf1[i+1]+
my_water_buf1[i-MY_WATER_W]+
my_water_buf1[i+MY_WATER_W])
>>1)
- my_water_buf2[i];
// 波能衰减
my_water_buf2[i] -= my_water_buf2[i]>>5;
}
p = my_water_buf1;
my_water_buf1 = my_water_buf2;
my_water_buf2 = p;
for (i=0; i<MY_WATER_W*MY_WATER_H; i++)
{
isrun = FALSE;
if (my_water_buf1[i] != 0)
{
isrun = TRUE;
break;
}
}
}
}
4 .渲染屏幕,这一步是很简单的,和网上是差不多的,直接拉来也可以使用,只是效率低一些,自己简单优化一下就会有很好的效率。
























 4279
4279

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








