粒子运动模拟 - Verlet积分算法简介

http://www.techbrood.com/zh/news/webgl/%E7%B2%92%E5%AD%90%E8%BF%90%E5%8A%A8%E6%A8%A1%E6%8B%9F---verlet%E7%A7%AF%E5%88%86%E7%AE%97%E6%B3%95%E7%AE%80%E4%BB%8B.html

Verlet算法是经典力学（牛顿力学）中的一种最为普遍的积分方法，被广泛运用在分子运动模拟（Molecular Dynamics Simulation），行星运动以及织物变形模拟等领域。Verlet算法要解决的问题是，给定粒子t时刻的位置r和速度v，得到t+dt时刻的位置r(t+dt)和速度v(t+dt)。最简单的方法是前向计算（考虑当前和未来）的速度位移公式，也就是显式欧拉方法，但精度不够，且不稳定。Verlet积分是一种综合过去、现在和未来的计算方法（居中计算），精度为O(4), 稳定度好，且计算复杂度不比显式欧拉方法高多少。

对于Verlet算法详细的介绍，可以参考维基百科：Verlet integration .

Verlet算法简要介绍

1. 将 x(t+Δt) 和 x(t-Δt) 进行泰勒展开

2. 将以上两个表达式进行相加，得到位置表达式

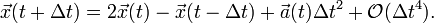
这个式子就显明，如果知道当前时刻的位置和加速度，前一时刻的位置，就可以推算出下一时刻的位置。

3. 将1中的两个式子相减，再同时除以 2Δt 即可获得速度表达式

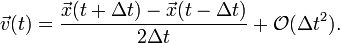
这个式子显明，只有在知道前一时刻和后一时刻的位置时，才有可能知道当前时刻的速度。也就是说，在当前时刻不能获得速度信息，必须要等到下一时刻的位置确定以后，才能返回来计算当前的速度。

4. 力（加速度）根据当前的位置 x(t)，基于一定的势函数进行更新

Verlet算法积分步运行过程

根据verlet算法，要计算t' ( = t+Δt)时刻的位置，必须知道 t'-2Δt 时刻和 t'-Δt 时刻的位置， t'-2Δt 的速度和 t'-Δt 时刻的加速度。具体演绎过程如下：

1. 根据 t'-Δt 和 t'-2Δt 时刻的位置、 t'-Δt 时刻的加速度 ，获得当前时刻 t' 的位置。

2. 根据当前时刻 t' 的位置，更新当前位置下的加速度（受力）。

3. 同时，可以更新 t'-Δt 时刻的速度。(速度是附带更新了，不更新速度并不妨碍积分过程继续下去。)

那么，现在就获得了 t' 时刻的位置， t'-Δt 时刻的速度和 t' 时刻的加速度，相当于将已知条件向前推进了一步（可以对比红色的部分）。

接下来的过程就是重复上面的过程。下图生动的反映了这个过程。

其中t表示时间，r表示位置，v表示速度，a表示加速度。