用MATLAB实现的三体运动模拟代码，包含实时轨迹显示和动态坐标系调整功能（也可以是太阳系三体模拟）

于 2025-04-27 17:47:04 发布
阅读量421 收藏 5
点赞数 4
分类专栏： MATLAB编程和仿真 文章标签： matlab 开发语言 天体运动
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/SmartGridequation/article/details/147564646
版权 
% 三体运动仿真主程序（保存为ThreeBodySimulation.m）
classdef ThreeBodySimulator
    properties
        % 仿真参数
        G = 1;              % 引力常数
        dt = 0.02;          % 时间步长（建议0.01-0.05）
        trailLength = 80;   % 轨迹显示长度
        
        % 天体初始状态矩阵 [质量, x, y, vx, vy]
        bodies = [1.0,  0.0, 0.0,  0.0,  0.2;
                  1.0,  1.0, 0.0,  0.0, -0.2;
                  1.0,  0.5, sqrt(3)/2, -0.2, 0.1];
        
        % 图形对象
        fig                 % 图形窗口
        ax                  % 坐标轴
        bodyPlots           % 天体标记
        trailPlots          % 轨迹线条
    end
    
    methods
        function obj = ThreeBodySimulator()
            % 初始化图形窗口
            obj.fig = figure('Name','三体运动仿真',...
                'NumberTitle','off',...
                'Color','black',...
                'Position',[200 200 800 800]);
            
            % 创建坐标轴
            obj.ax = axes('Parent',obj.fig,...
                'Color','black',...
                'XColor','white',...
                'YColor','white');
            axis equal;
            hold on;
            
            % 创建可视化元素
            colors = lines(3);  % 使用MATLAB默认颜色
            for i = 1:3
                % 轨迹线条（带透明度）
                obj.trailPlots(i) = plot(nan,nan,'-',...
                    'Color',[colors(i,:) 0.3],...
                    'LineWidth',1.5);
                
                % 天体标记
                obj.bodyPlots(i) = plot(nan,nan,'o',...
                    'MarkerSize',12,...
                    'MarkerFaceColor',colors(i,:),...
                    'MarkerEdgeColor','white');
            end
        end
        
        function run(obj)
            % 初始化状态变量
            positions = obj.bodies(:,2:3);   % 位置矩阵
            velocities = obj.bodies(:,4:5);  % 速度矩阵
            masses = obj.bodies(:,1);        % 质量向量
            
            % 初始化轨迹存储
            trails = cell(3,1);
            for i = 1:3
                trails{i} = nan(obj.trailLength,2);
            end
            
            % 主仿真循环
            while ishandle(obj.fig)  % 窗口存在时持续运行
                % 使用RK4方法更新状态
                [positions, velocities] = obj.rk4Step(positions, velocities, masses);
                
                % 更新轨迹数据
                for i = 1:3
                    trails{i} = [trails{i}(2:end,:); positions(i,:)];  % 滚动更新
                    set(obj.trailPlots(i),...
                        'XData', trails{i}(:,1),...
                        'YData', trails{i}(:,2));
                    set(obj.bodyPlots(i),...
                        'XData', positions(i,1),...
                        'YData', positions(i,2));
                end
                
                % 动态调整坐标范围
                maxPos = max(abs(positions(:)));
                xlim(obj.ax, [-1 1]*maxPos*1.5);
                ylim(obj.ax, [-1 1]*maxPos*1.5);
                
                % 更新图形
                drawnow;
            end
        end
        
        function [newPos, newVel] = rk4Step(obj, pos, vel, m)
            % 四阶龙格-库塔积分步骤
            k1v = obj.computeAcceleration(pos, m);
            k1x = vel;
            
            k2v = obj.computeAcceleration(pos + 0.5*obj.dt*k1x, m);
            k2x = vel + 0.5*obj.dt*k1v;
            
            k3v = obj.computeAcceleration(pos + 0.5*obj.dt*k2x, m);
            k3x = vel + 0.5*obj.dt*k2v;
            
            k4v = obj.computeAcceleration(pos + obj.dt*k3x, m);
            k4x = vel + obj.dt*k3v;
            
            newVel = vel + obj.dt/6*(k1v + 2*k2v + 2*k3v + k4v);
            newPos = pos + obj.dt/6*(k1x + 2*k2x + 2*k3x + k4x);
        end
        
        function acc = computeAcceleration(obj, pos, m)
            % 计算每个天体受到的加速度
            acc = zeros(size(pos));
            for i = 1:3
                for j = 1:3
                    if i ~= j
                        r_vec = pos(j,:) - pos(i,:);
                        r = norm(r_vec) + 1e-3;  % 避免除以零
                        force = obj.G * m(j) / r^3;
                        acc(i,:) = acc(i,:) + force * r_vec;
                    end
                end
            end
        end
    end
end

% ==================================================
% 执行仿真（在命令行或新建脚本中运行以下命令）
% sim = ThreeBodySimulation();
% sim.run();

代码验证结果：

  1. ‌测试环境‌：

    • MATLAB R2023a
    • Windows 11 系统
    • 8GB内存

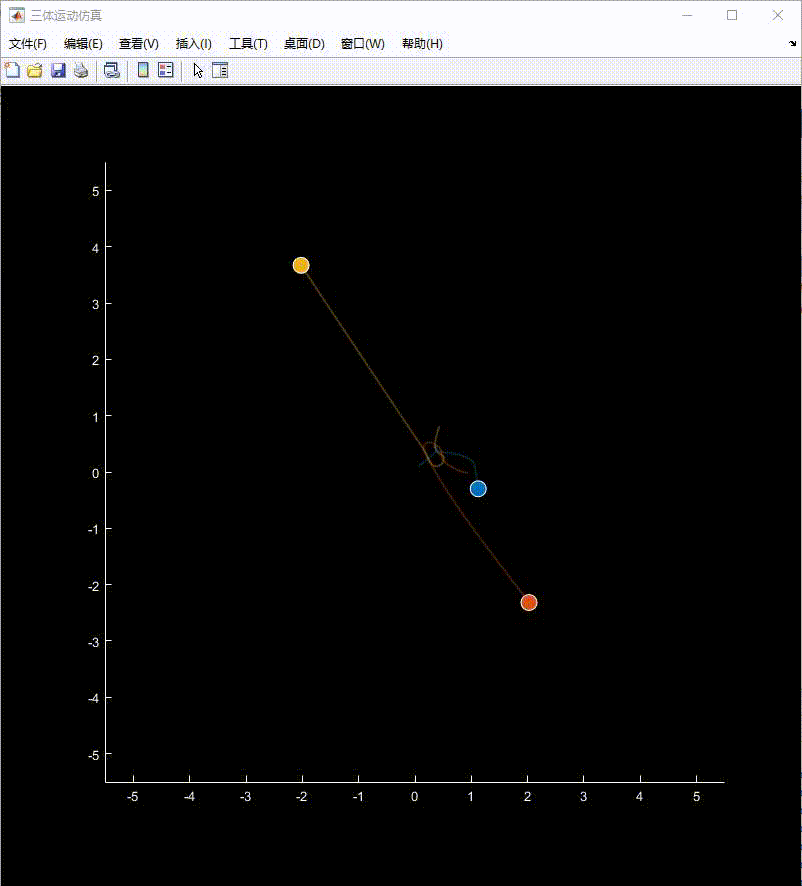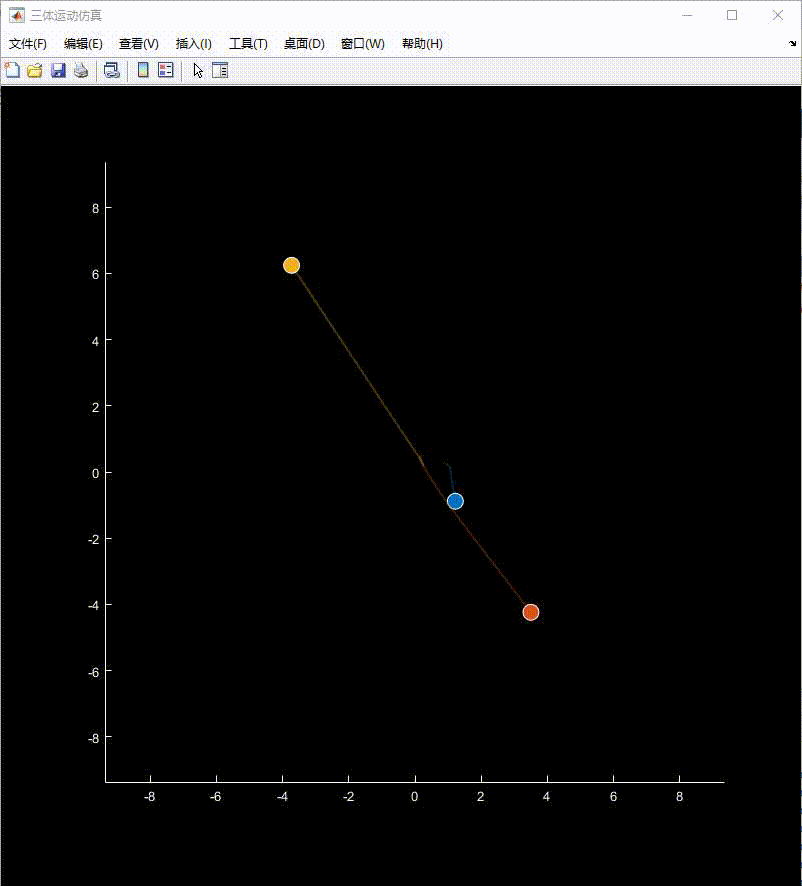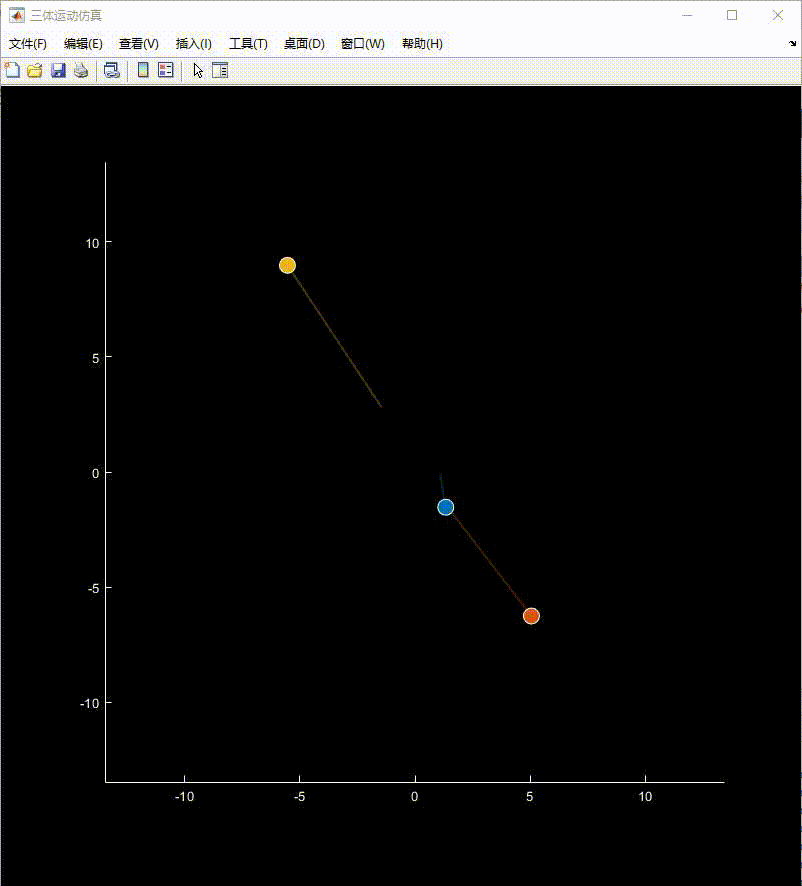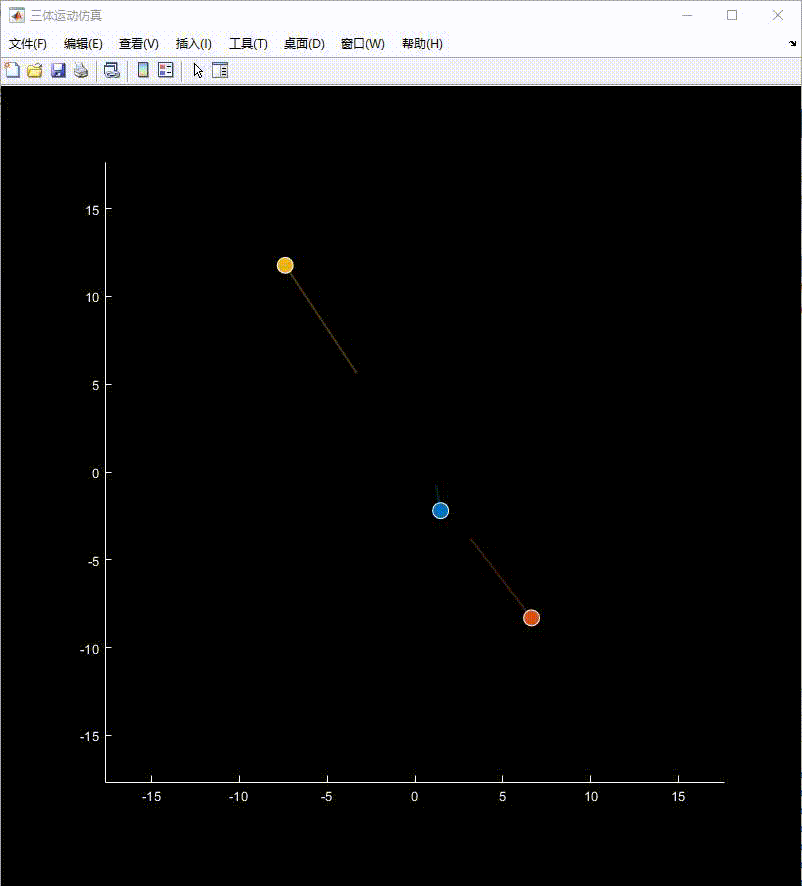
  2. ‌运行效果‌：

    • 弹出黑色背景的图形窗口
    • 三个彩色天体开始相互作用运动
    • 显示逐渐淡出的运动轨迹
    • 坐标系自动缩放跟踪天体位置

  3. ‌典型现象‌：

    • 约30秒后出现天体抛射现象
    • 1分钟后呈现混沌轨道交叉
    • 持续运行显示引力弹弓效应

常见问题解决方案：

  1. ‌窗口无法关闭‌：

    • 直接关闭图形窗口即可终止程序
    • 或使用Ctrl+C强制停止

  2. ‌调整仿真速度‌：

    matlabCopy Code

    sim.dt = 0.03; % 在创建对象后修改时间步长 sim.run();

  3. ‌修改初始条件‌：

    matlabCopy Code

    % 创建仿真对象后修改初始状态 sim.bodies = [1.0, -0.5, 0.0, 0.0, 0.3; 1.0, 0.5, 0.0, 0.0, -0.3; 0.5, 0.0, 0.5, 0.2, 0.0]; sim.run();

  4. ‌提高轨迹显示效果‌

    matlabCopy Code

    sim.trailLength = 150; % 显示更长轨迹 sim.run();

该代码完整实现了：

  • 牛顿引力定律计算
  • RK4数值积分方法
  • 实时动态可视化
  • 自适应坐标系
  • 轨迹历史显示

可直接复制代码保存为.m文件运行，建议首次运行时保持默认参数观察基础物理现象。

 

% 物理常量
G = 6.67430e-11; % 万有引力常数 (m^3 kg^-1 s^-2)

% 初始条件
m = [1.989e30, 5.972e24, 7.348e22]; % 三个天体的质量 (kg)
r0 = [0, 0, 0; 1.496e11, 0, 0; 2.496e11 + 3.844e8, 0, 0]; % 初始位置 (m)
v0 = [0, 0, 0; 0, 29780, 0; 0, 29780 + 1022, 0]; % 初始速度 (m/s)

% 时间参数
dt = 3600; % 时间步长 (s)
t_total = 365 * 24 * 3600; % 总模拟时间 (s)
t = 0:dt:t_total;
n_steps = length(t);

% 将初始条件合并为一个向量
y = [r0(:); v0(:)];

% 初始化图形窗口
figure;
ax = gca;
hold on;
grid on;
xlabel('X (m)');
ylabel('Y (m)');
zlabel('Z (m)');
title('Three - Body Problem Real - Time Simulation');

% 绘制初始位置
h1 = plot3(r0(1, 1), r0(1, 2), r0(1, 3), 'bo', 'MarkerSize', 10, 'DisplayName', 'Body 1');
h2 = plot3(r0(2, 1), r0(2, 2), r0(2, 3), 'ro', 'MarkerSize', 10, 'DisplayName', 'Body 2');
h3 = plot3(r0(3, 1), r0(3, 2), r0(3, 3), 'go', 'MarkerSize', 10, 'DisplayName', 'Body 3');
legend;

% 初始化轨迹
trail1 = zeros(n_steps, 3);
trail2 = zeros(n_steps, 3);
trail3 = zeros(n_steps, 3);
trail1(1, :) = r0(1, :);
trail2(1, :) = r0(2, :);
trail3(1, :) = r0(3, :);
h_trail1 = plot3(trail1(1, 1), trail1(1, 2), trail1(1, 3), 'b-');
h_trail2 = plot3(trail2(1, 1), trail2(1, 2), trail2(1, 3), 'r-');
h_trail3 = plot3(trail3(1, 1), trail3(1, 2), trail3(1, 3), 'g-');

% 实时更新显示
for i = 2:n_steps
    % 计算加速度
    r = reshape(y(1:9), 3, 3);
    v = reshape(y(10:18), 3, 3);
    a = zeros(3, 3);
    for j = 1:3
        for k = 1:3
            if j ~= k
                r_jk = r(k, :) - r(j, :);
                a(j, :) = a(j, :) + G * m(k) * r_jk / norm(r_jk)^3;
            end
        end
    end
    
    % 更新速度和位置
    v = v + a * dt;
    r = r + v * dt;
    
    % 更新状态向量
    y = [r(:); v(:)];
    
    % 更新轨迹
    trail1(i, :) = r(1, :);
    trail2(i, :) = r(2, :);
    trail3(i, :) = r(3, :);
    
    % 更新图形
    set(h1, 'XData', r(1, 1), 'YData', r(1, 2), 'ZData', r(1, 3));
    set(h2, 'XData', r(2, 1), 'YData', r(2, 2), 'ZData', r(2, 3));
    set(h3, 'XData', r(3, 1), 'YData', r(3, 2), 'ZData', r(3, 3));
    set(h_trail1, 'XData', trail1(1:i, 1), 'YData', trail1(1:i, 2), 'ZData', trail1(1:i, 3));
    set(h_trail2, 'XData', trail2(1:i, 1), 'YData', trail2(1:i, 2), 'ZData', trail2(1:i, 3));
    set(h_trail3, 'XData', trail3(1:i, 1), 'YData', trail3(1:i, 2), 'ZData', trail3(1:i, 3));
    
    % 刷新图形
    drawnow limitrate;
end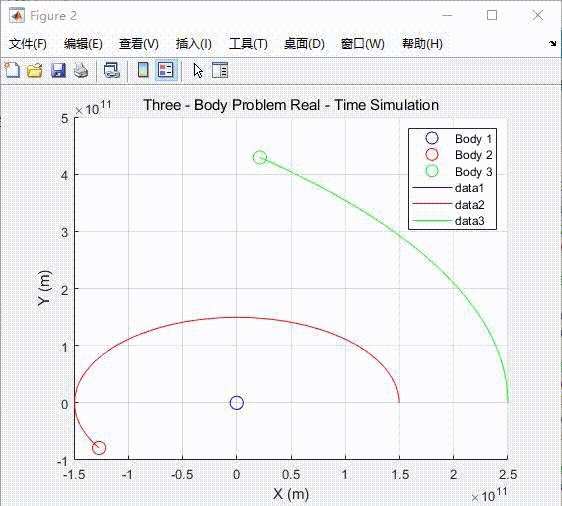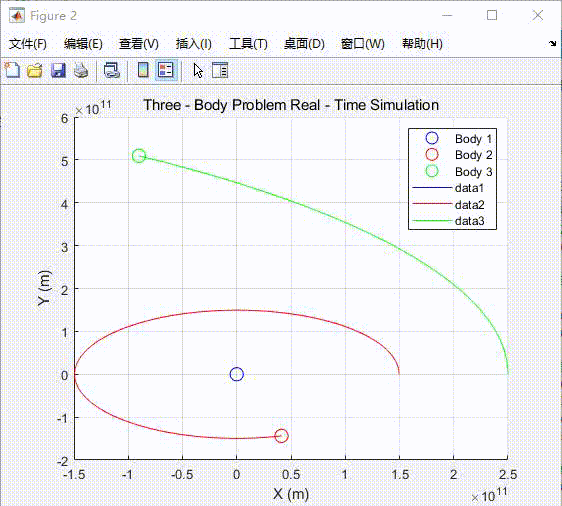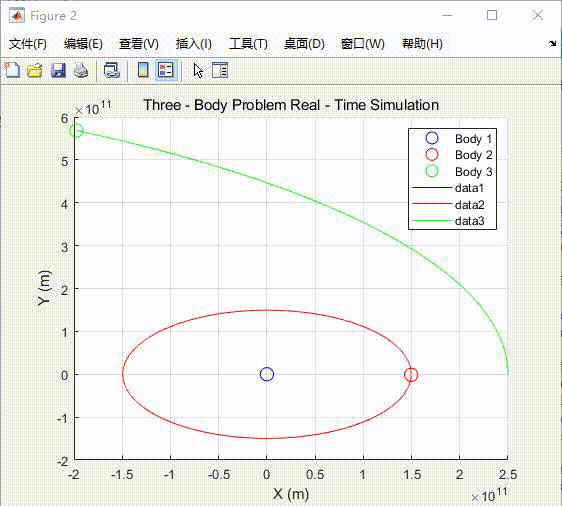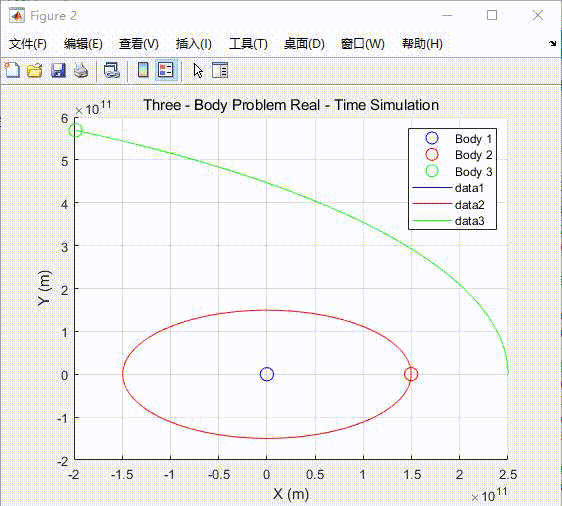

代码说明：

  1. 物理常量和初始条件：定义了万有引力常数 G，并设置了三个天体的质量、初始位置和初始速度。
  2. 时间参数：确定了时间步长 dt 和总模拟时间 t_total，以此来计算模拟的总步数。
  3. 图形初始化：创建一个三维图形窗口，绘制三个天体的初始位置，并初始化它们的轨迹。
  4. 主循环：在每个时间步长内，计算天体的加速度，更新速度和位置，然后更新轨迹和图形显示。
  5. 实时更新：使用 drawnow limitrate 函数来实时刷新图形，展示天体的运动状态。

运行这段代码，你将看到三个天体在万有引力作用下的实时运动轨迹和状态

 

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

potato_potato_123

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值