卫星变轨轨迹和推力模拟（单一引力源）MATLAB

 

代码说明：

1. 常量定义：定义了万有引力常数、地球和月球的质量、半径以及地月平均距离。
2. 初始状态设置：设置卫星的初始位置、速度和姿态，以及月球的初始位置。
3. 模拟循环：在循环中计算地球和月球对卫星的引力，模拟机动变轨推力，更新卫星的速度、位置和姿态。
4. 绘制 3D 场景：卫星轨迹、卫星姿态和推力矢量。
5. 辅助函数：rotationMatrix 函数用于计算旋转矩阵，drawSatellite 函数用于绘制卫星（长方体）。

你可以根据需要调整模拟参数和卫星的初始状态。

% 常量定义
G = 6.67430e-20; % 万有引力常数 (km^3 kg^-1 s^-2)
M_earth = 5.972e12; % 地球质量 (kg)

% 卫星初始状态
initial_position = [5; 0; 0]; % 初始位置 (km)，椭圆轨道长半轴的端点
initial_velocity = [0; 2; 0]; % 初始速度 (km/s)，垂直于长半轴方向
initial_attitude = [1 0 0; 0 1 0; 0 0 1]; % 初始姿态矩阵

% 引力源位置（假设在原点）
gravitational_source_position = [0; 0; 0];

% 模拟参数
total_time = 200; % 总模拟时间 (s)，根据椭圆轨道周期调整
dt = 0.1; % 时间步长 (s)
num_steps = total_time / dt;

% 初始化数组
position = zeros(3, num_steps);
velocity = zeros(3, num_steps);
attitude = zeros(3, 3, num_steps);

position(:, 1) = initial_position;
velocity(:, 1) = initial_velocity;
attitude(:, :, 1) = initial_attitude;

% 椭圆轨道参数
semi_major_axis = norm(initial_position); % 长半轴
angular_velocity = norm(initial_velocity) / semi_major_axis; % 角速度

% 模拟循环
for i = 1:num_steps - 1
    % 计算引力
    r = position(:, i) - gravitational_source_position;
    gravitational_force = -G * M_earth * r / norm(r)^3;
    
    % 计算当前位置的角度
    current_angle = atan2(position(2, i), position(1, i));
    
    % 计算向心力方向的单位向量
    centripetal_direction = -position(:, i) / norm(position(:, i));
    
    % 计算向心力大小（根据圆周运动公式 F = m * v^2 / r，这里假设 m = 1）
    centripetal_magnitude = norm(velocity(:, i))^2 / norm(position(:, i));
    
    % 计算推力
    thrust = centripetal_direction * centripetal_magnitude;
    
    % 计算总加速度
    acceleration = gravitational_force + thrust;
    
    % 更新速度和位置
    velocity(:, i + 1) = velocity(:, i) + acceleration * dt;
    position(:, i + 1) = position(:, i) + velocity(:, i) * dt;
    
    % 更新姿态（这里简单假设姿态绕推力方向旋转一个小角度）
    rotation_angle = 0.001; % 旋转角度 (rad)
    rotation_axis = thrust / norm(thrust);
    rotation_matrix = rotationMatrix(rotation_axis, rotation_angle);
    attitude(:, :, i + 1) = rotation_matrix * attitude(:, :, i);
end

% 绘制 3D 轨迹
figure;
plot3(position(1, :), position(2, :), position(3, :), 'b', 'LineWidth', 2);
xlabel('X (km)');
ylabel('Y (km)');
zlabel('Z (km)');
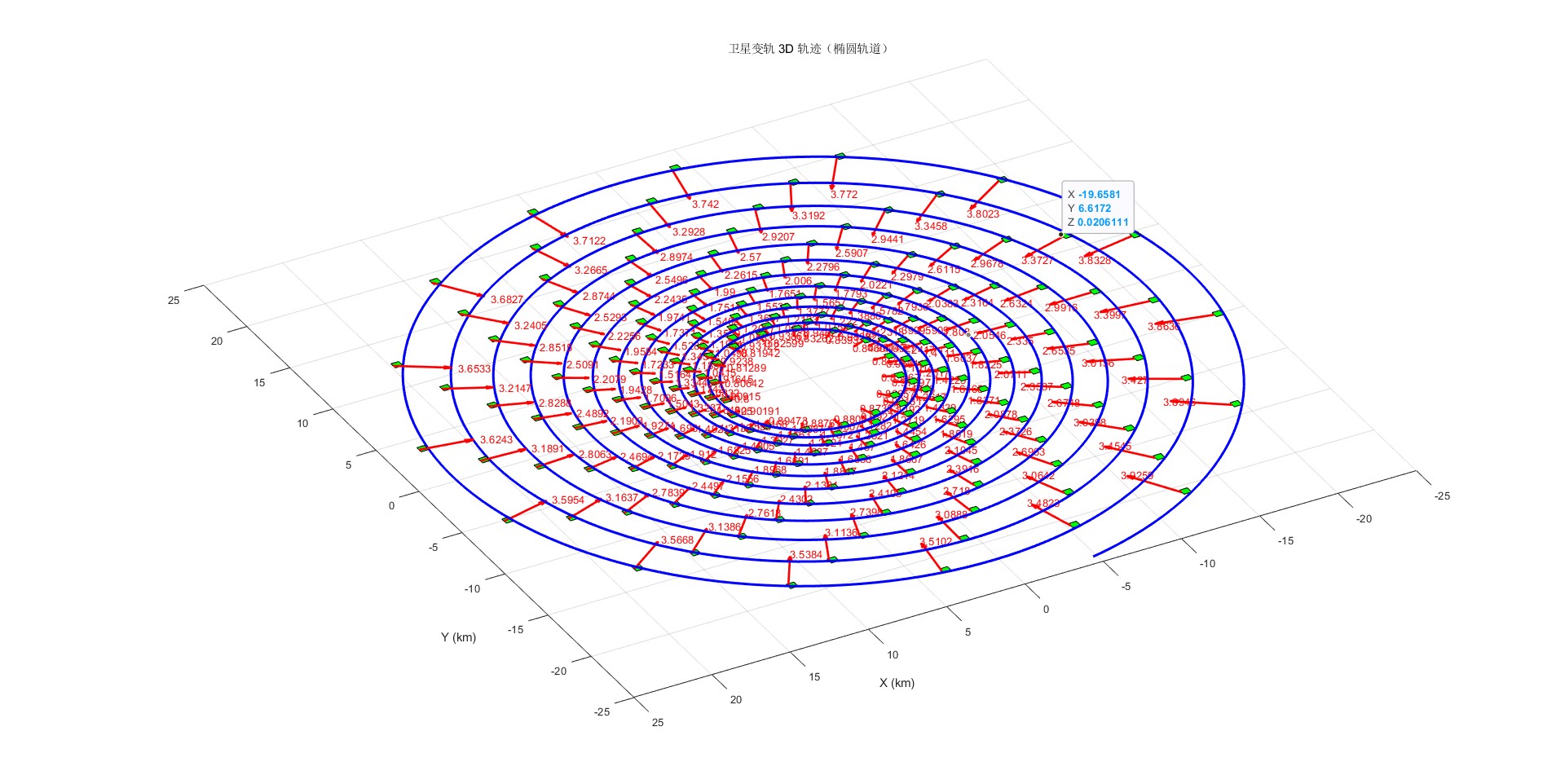
title('卫星变轨 3D 轨迹（考虑引力源）');
grid on;

% 绘制卫星姿态和推力矢量
for i = 1:10:num_steps
    % 绘制卫星（长方体）
    drawSatellite(position(:, i), attitude(:, :, i));
    
    % 确定立方体底面中心位置
    length = 1;
    width = 0.5;
    height = 0.2;
    base_center_local = [length/2; width/2; 0];
    base_center_global = attitude(:, :, i) * base_center_local + position(:, i);
    
    % 计算当前位置的角度
    current_angle = atan2(position(2, i), position(1, i));
    
    % 计算向心力方向的单位向量
    centripetal_direction = -position(:, i) / norm(position(:, i));
    
    % 计算向心力大小（根据圆周运动公式 F = m * v^2 / r，这里假设 m = 1）
    centripetal_magnitude = norm(velocity(:, i))^2 / norm(position(:, i));
    
    % 计算推力
    thrust = centripetal_direction * centripetal_magnitude;
    
    % 绘制推力矢量
    quiver3(base_center_global(1), base_center_global(2), base_center_global(3), thrust(1), thrust(2), thrust(3), 'r', 'LineWidth', 2, 'MaxHeadSize', 0.5);
    % 标注矢量大小
    text(base_center_global(1)+thrust(1), base_center_global(2)+thrust(2), base_center_global(3)+thrust(3), num2str(centripetal_magnitude), 'Color', 'r');
end

% 旋转矩阵函数
function R = rotationMatrix(axis, angle)
    axis = axis / norm(axis);
    c = cos(angle);
    s = sin(angle);
    t = 1 - c;
    x = axis(1);
    y = axis(2);
    z = axis(3);
    
    R = [t*x^2 + c    t*x*y - s*z  t*x*z + s*y;
         t*x*y + s*z  t*y^2 + c    t*y*z - s*x;
         t*x*z - s*y  t*y*z + s*x  t*z^2 + c];
end

% 绘制卫星（长方体）函数
function drawSatellite(position, attitude)
    % 长方体尺寸
    length = 1;
    width = 0.5;
    height = 0.2;
    
    % 长方体顶点坐标
    vertices = [0 0 0;
                length 0 0;
                length width 0;
                0 width 0;
                0 0 height;
                length 0 height;
                length width height;
                0 width height];
    
    % 应用姿态变换
    vertices = vertices * attitude';
    
    % 平移到当前位置
    vertices = bsxfun(@plus, vertices, position');
    
    % 绘制长方体
    faces = [1 2 3 4; 5 6 7 8; 1 2 6 5; 2 3 7 6; 3 4 8 7; 4 1 5 8];
    patch('Vertices', vertices, 'Faces', faces, 'FaceColor', 'g', 'EdgeColor', 'k');
    hold on;
end