周志华《机器学习》课后习题解答系列（六）：Ch5.10 - 卷积神经网络实验

本系列相关答案和源代码托管在我的Github上：PY131/Machine-Learning_ZhouZhihua.

卷积神经网络实验 - 手写字符识别

注：本题程实现基于python-theano（这里查看完整代码和数据集）。

1. 基础知识回顾

1.1. 核心思想

卷积神经网络（Convolutional Neural Network, CNN）是“深度学习”的代表模型之一，是一种多隐层神经网络，正被广泛用于图像处理、语音识别等热点领域。

卷积神经网络的原理和特点，集中体现在以下三个核心思想当中：

• 局部感受野（Local Receptive Fields）
• 权值共享（weight sharing）
• 时间或空间的亚采样

在整合了上述三大特点之后，卷积神经网络具备了很强的畸变容忍能力，能够从复杂的对象中隐式地进行特征提取与学习。

1.2. 结构和功能

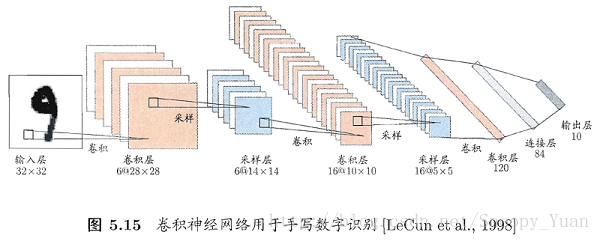
卷积神经网络同多层感知机（MLP）一样，通过设置多个隐层来实现对复杂模型的学习。如下图所示是一个手写字符识别的卷积神经网络结构示意图（书p114）：

从图中可以看到卷积层（convolutional layer）和采样层（pooling layer）的复合，其功能简述如下：

• 卷积层包含多个特征映射（feature map），它们采用相应的卷积滤波器从输入中提取特征；
• 采样层基于局部相关性原理对卷积层进行亚采样，从而在保留有用信息的同时减少数据量；

通过多层复合，隐层最终输出目标维特征向量，通过连接层和输出层输出结果。

1.3. 参数技巧

神经网络的参数设计十分重要，关于CNN模型的一些参数的考虑（如隐层特征图数目和大小、滤波器大小等），可参考Convolutional Neural Networks (LeNet)文章最后Tips and Tricks的内容。

2. 手写字符识别实验

这里，我们采用python-theano深度学习库来实现基于MNIST数据的字符识别实验。关于theano的基础使用可参考：深度学习基础 - 基于Theano-MLP的字符识别实验（MNIST）或是Deep Learning Tutorials。

2.1. 数据获取及预处理

这里我们采用经过规约的数据集mnist.pkl.gz,给出该数据集的部分信息如下：