ST表：解决区间最大值问题

ST表（Sparse Table，稀疏表）

ST表是一种基于倍增思想，用于解决可重复贡献问题的数据结构。

ST表应用最广泛的领域便是解决RMQ问题（区间最值查询）：

给定n个数，m个询问，对于每个询问，需要回答区间中的最值。

以最大值为例，ST表使用一个二维数组，对于范围内的所有，先进行预处理，计算并存储

本文中区间都是离散意义下的，只包含整数，所以也可以写成：

查询时，再利用这些子区间算出待求区间的最大值。

预处理时间复杂度为O(nlogn)，查询时间为O(1)。

---

ST表原理

表示区间中的最小值（显然这是下标范围）

将区间分为前后两端，则任意一段的最大值显然等于

（前半段的最大值，后半段的最大值）

我们来推导一下的状态转移方程：

从到的长度为​​，那么一半的长度为即

那么前半段最值的区间

状态表示为：

后半段区间为，右边式子改写为

状态表示为：

所以

采用位运算的方式进行处理，提高效率：

int st[maxn][30] //列数一般不小于log2(maxn)即可
for(int i = 1; i <= n; i++){
  st[i][0] = read();//读入数据
}
for(int j = 1; j <= 30; i++){
  for(int i = 1; i + (1 << j) - 1 <= n; i++){
     st[i][j] = max(st[i][j - 1],st[i + (1 << (j - 1))][j - 1]);
   } 
}

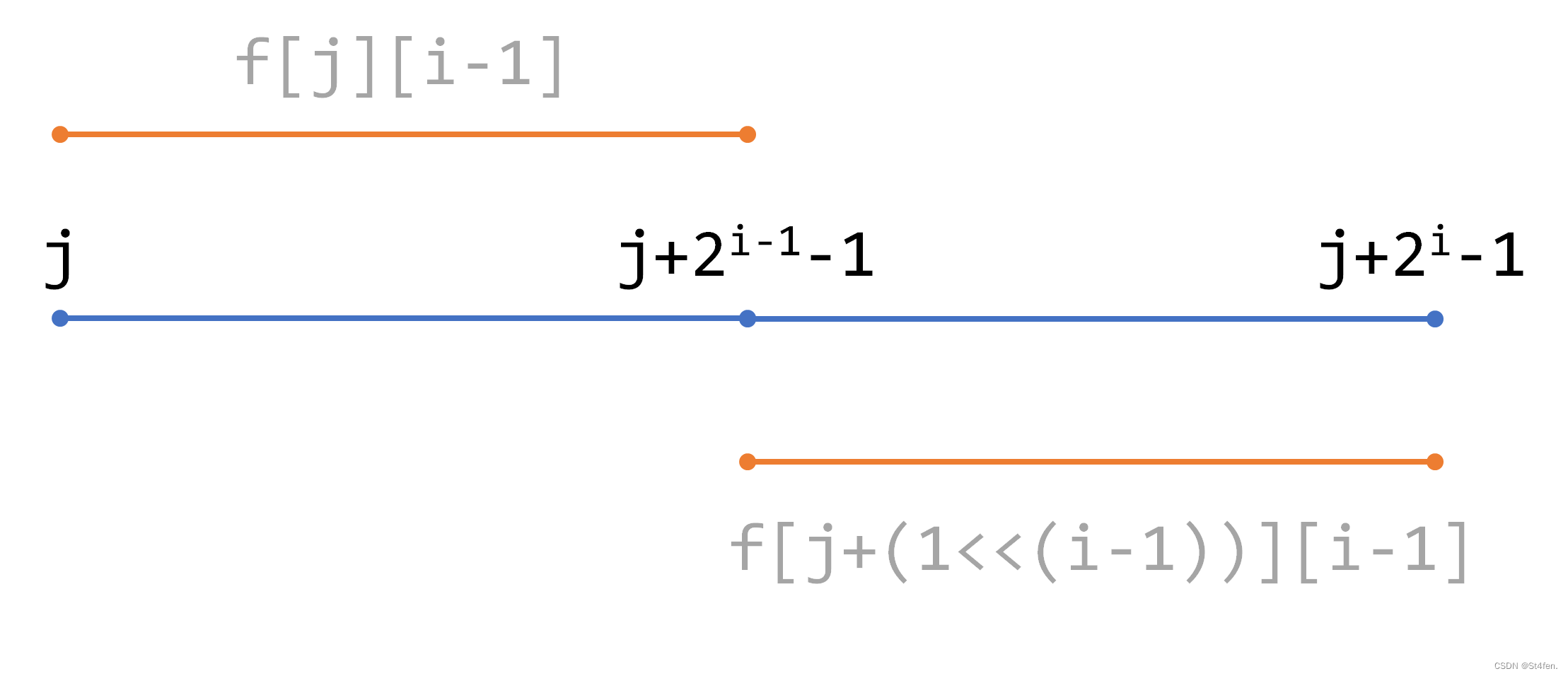
左边子区间取最大值，右边子区间取最大值，再取两个子区间的最大值

---

 查询

查询时，需要找到目标区间[l,r][l,r][l,r]的两个子区间，使他们的并集为(不必不相交)。具体地，就是要找到一个整数，两个子区间分别为和。

 我们希望前一个子区间的右端点尽可能接近r（同样会使第二个子区间的左端点尽可能接近）。当时，有 。

由于是整数，我们取。可以证明，此时两个子区间确实可以覆盖。

//计算s:
int s = log(r - l + 1) / log 2;

 每次计算值太花时间了，我们同样可以进行一次递推的预处理：

int logn[maxn] = {-1};
for(int i = 1; i <= n; i++){
    logn[i] = logn[i / 2]  + 1;
}

 在线查询的代码如：

int queMax(int l, int r){
    int k = logn[r - l + 1];
    return max(st[l][k], st[r - (1<<k) + 1][k]);
}

---

洛谷模板题： 【模板】ST 表 - 洛谷

给出一道模板题进行练习，下面是我的AC代码

#include <iostream>
#include <string> 
#include <cmath>
using namespace std;

inline int read(){
	int x = 0, f = 1; 
	char ch = getchar();
	while(ch < '0' || ch > '9'){
		if(ch == '-')
			f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9'){
		x = x * 10 + ch - 48;
		ch = getchar();
	}
	return x * f;
}

long long n, m;
const int maxn = 1e5 + 9;
long long st[maxn][20];
long long logn[maxn] = {-1};
long long l, r;

long long queMax(long long l, long long r){
	int k = logn[r - l + 1];
	return max(st[l][k], st[r - (1<<k) + 1][k]);
}

int main(){
	n = read();
	m = read();
	for(long long i = 1; i <= n; i++){
		st[i][0] = read();
		logn[i] = logn[i / 2] + 1;
	}
	for(long long j = 1; j <= 20; j++){
		for(long long i = 1; i + (1 << j) - 1 <= n; i++){
			st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
		}
	}
	for(long long i = 1; i <= m; i++){
		l = read();
		r = read();
		cout<<queMax(l,r)<<'\n';
	}
}

ST表优点：时间复杂度较低 、代码量较少。

ST表缺点：维护的信息有限，只支持静态操作（不支持修改操作）。

---

可重复贡献问题

凡是符合结合律且可重复贡献的信息查询都可以使用ST表高效进行。

可重复贡献问题是对于一个二元运算，运算的性质满足

例如：最大值满足，最大公因数。

显然最大值、最小值、最大公因数、最小公倍数、按位或、按位与都符合这个条件。可重复贡献的意义在于，可以对两个交集不为空的区间进行信息合并。