子字符串查找（上）：从暴力算法到KMP

子字符串查找(串匹配)很常用，当你在文本编辑器中使用搜索功能定位某个单词，或者在浏览器中输入一个关键字搜索网页，你可能从未意识到此时你正面临的就是子字符串查找问题。你得到了想要的结果，而这背后起作用的就是某一个子字符串查找算法。

问题描述：
文本T = Life becomes a lot more fun when you know that it is meaningless
模式P = fun

将文本串的长度记作N，即N = |T|；模式串的长度记作M，即M = |P|。通常有N >> M >> 1

问题已经清楚了，那么有哪些策略可以用来解决这个问题呢？

首先最容易想到的就是暴力解法：将文本串和模式串的首字符对齐，依次比对每一个字符，若在某一位置比对失败，将模式串自左向右移动一个单位，重新开始新一轮的比较。

具体实现：定义两个指针，指针i跟踪文本，指针j跟踪模式，将逻辑上的模式串自左向右移动转化为：把指针i指向的位置作为与模式串匹配的起始位置，i的取值范围为[0,N-M]。在每一个特定的i将其后（包含i本身）长度为j的子串依次与模式串的每个字符比对，当出现不同字符时，将j重置为0，i向后移动一个单位，不断重复这一过程，直至i越界（匹配失败）或者当匹配成功时返回i的位置。

代码如下：

public static int search(String txt, String pat) {
        int N = txt.length();
        int M = pat.length();
        for (int i = 0; i <= N - M; i++) {
            int j;
            for (j = 0; j < M; j++) {
                if (txt.charAt(i + j) != pat.charAt(j)) {
                    break;
                }
            if (j == M) return i;//匹配成功
            }
        }
        return N;//匹配失败
}

暴力算法的正确性毋庸置疑，它的效率怎么样呢？

最好情况：对于每一特定的i在起始位置就与模式串不匹配，在这种情况下只需N-M+1次比较，即O(N)；

最坏情况：对于某一特定的i,在与模式串比对过程中，前M-1项皆匹配成功，第M项比对失败，也就是说文本串中的每个字符都与模式串中的每一个字符比对一次，在这种情况下需要进行（N-M+1）* M次比较，即O(N*M)；

对于一个算法我们通常考虑其最坏情况，因为它给出了算法运行时间的上界，即为我们提供了一个保证：该算法在任何情况下的运行时间都不会大于该上界。

O（N*M）显然是不能接受的，我们想要的是即使在最坏情况下也能在线性时间内完成子字符串查找的算法。

稍加思考，不难发现，暴力解法每次只向右移动一个字符，这是制约该算法性能的主要原因，能不能突破这个瓶颈呢？答案是肯定的。

针对暴力解法的不足，KMP算法进行了两处改进：

1. 一次右移多个字符
2. 避免已匹配的字符串重复比对

KMP算法是如何做到这两点的呢？KMP提前构造了一张查询表。美妙的是查询表的构建与文本串无关，使得我们可以根据模式串提前构造查询表，KMP也因此具有了预知功能，这是KMP算法即使在最坏情况下也能在O(N)时间内完成子字符串查找的主要原因。

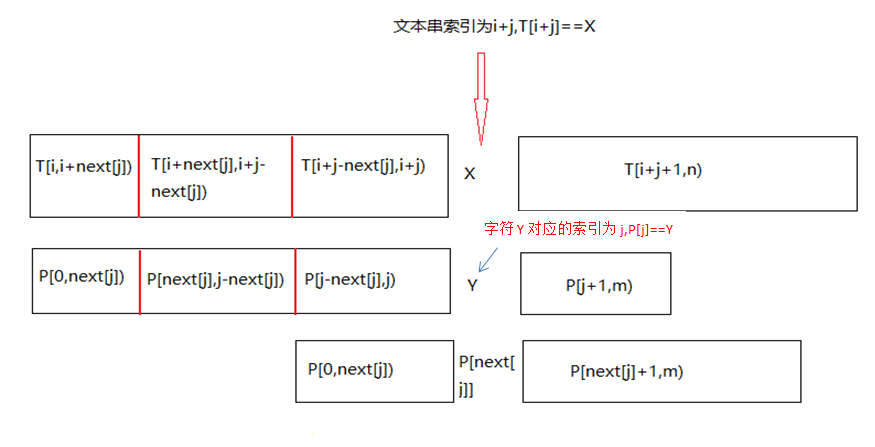
为什么查询表的构建与文本串无关呢？如下图所示，在P[j]之前模式串与文本串完全相等（长度记作partial_match_length），因此，我们可以只考虑模式串。再进一步，前缀是由P[j]决定的，只需对j构建next表（查询表），而j的取值范围不过是[0,M)。

j为模式串的索引，j == partial_match_length（例：j=3时考虑的是模式串中的前3个字符P[0,3)）。

以next[j] == 3为例：一次向右滑动partial_match_length - 3个位置，也就是说将P[next[j]]移动到P[j]，即P[j] = P[next[j]]，这一操作实现了一次右移多个字符。又因为相对于P[j]的前缀，其首部和尾部具有一定的相似性，已知P[0,next[j])与P[j-next[j],j)完全匹配，即可从P[j]处重新开始比对。

令最大自匹配的真前缀和真后缀的长度为t；KMP算法能够快速滑过j-2t个字符，避免重复比对t个字符。

综上，模式串与文本串在某一位置匹配失败后，KMP算法能告诉我们应该将模式串中的哪个字符移动到比对失败处，并且从失败处重新开始下一轮的比对。

既然next表决定了KMP算法的走向，那么next表应该如何构建呢？表中的每一项又有什么具体含义呢？

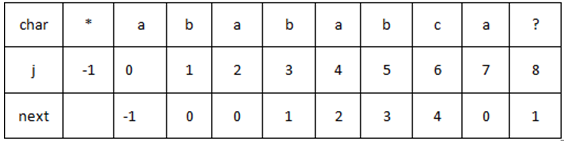
模式串P=abababca

next[j]代表什么？next[j]的值是模式串中长度为partial_match_length的子字符串真前缀与真后缀完全匹配的最大长度。模式串中partial_match_length为0的子串（首字符的前缀）为空，令next[0] = -1.

j=6，即partial_match_length=6,对应的子字符串为：ababab所有真前缀为：a,ab,aba,abab,ababa；所有真后缀为：babab,abab,bab,ab,b.可得真前缀与真后缀完全匹配的最大长度为4(abab)，所以next[6] = 4.

这里使用了一个小技巧：在模式串的左端设置一个哨兵，索引为-1，字符是一个通配符，能够匹配所有的字符。这样做的有两个好处：保持算法逻辑上的统一；使算法更加简洁。

计算next[j+1]时，当P[j]不等于P[next[j]]以及后续许多P[next of next of next of … next[j]]，最后收敛于1+next[0]，若next[0] == 0，P[next[0]] == P[0] != P[j]，需要单独对这种情况进行处理，算法的逻辑和实现都更加复杂。以计算next[j+1] (j=6为例)：

P[6] == c != P[next[6]] == a，计算P[next[next[6]]] == P[2] == a != c，计算P[next[next[next[6]]]] == P[0] == a != c，接着计算P[next[next[next[next[6]]]]] == P[-1] == c 推出next[7] = 1 + next[0],即next[7]=0;

观察这个计算过程， P[0] == a != c如果不设置哨兵，这种情况该怎么处理呢？（体会一下设置哨兵的妙处）

知道了next表的含义，接下来就该从代码的角度构建next表了：

已知next[0,j]，计算next[j+1]。当P[j] == P[next[j]]，next[j+1] = next[j] + 1;当P[j] != P[next[j]]，依次比对P[j]与P[next[next[j]]]…最坏的情况收敛于P[j] == P [next[0]]，此时next[j+1] = 1 + next[0];

next表的构建代码如下：

public static int buildNext(String pat) {
        int M = pat.length();
        int j = 0;
        int[] next = new int[M];
        next[0] = -1;
        while (j < M -1) {
            if (0 > next[j] || pat.charAt(j) == pat.charAt(next[j])) {
                next[++j] = ++next[j];
            } else {
                next[j] = next[next[j]];
            }
        }
        return M;
}

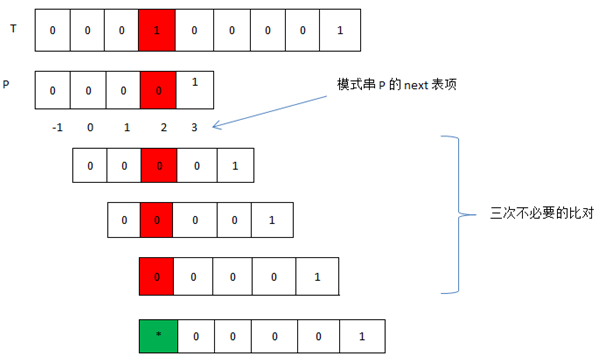
KMP算法很聪明，那么它是完美的吗？至少现在我们的KMP算法还有改进的空间。看下面一种情况：

当P[j] != T[I + j]时,用P[next[j]]替换P[j]，观察上图可知多了三次不必要的比对，能不能避免这种情况呢？问题出在了哪里呢？

用来替换P[j]的P[next[j]]和P[j]相等，匹配会继续失败。

对于匹配失败处的字符，KMP能告诉我们它应该是什么，如果它也能告诉我们不应该是什么，那么上面例子中的三次不必要的比对就可以避免。

改进后的KMP算法如下:

public static int buildNextElevate(String pat) {
        int M = pat.length();
        int j = 0;
        int[] next = new int[M];
        next[0] = -1;
        while (j < M -1) {
            if (0 > next[j] || pat.charAt(j) == pat.charAt(next[j])) {
                j++; next[j]++;
                next[j] = pat.charAt(j) != pat.charAt(next[j]) ? next[j] : next[next[j]];//与前一版本的不同之处
            } else {
                next[j] = next[next[j]];
            }
        }
        return M;
}

在最坏情况下，暴力算法确实很慢，但它真的一无是处吗？

首先，它能正确的解决问题，其次，它为我们提供了优化的思路和方向。对于很多问题，暴力解法往往不是最优的，但它却是一个很好的开始。

PS:
The Knuth-Morris-Pratt Algorithm in my own words