Kalman filter 卡尔曼公式推导

已于 2022-10-26 16:44:44 修改
阅读量188 收藏 2
点赞数 1
分类专栏： 卡尔曼滤波器 文章标签： 算法 概率论 矩阵
于 2022-10-18 11:42:19 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Strong__M/article/details/127384408
版权

Kalman filter

前言

最近学习了卡尔曼滤波器，所以整理在上面，之后如果有用到的话再看，这里就不再做前沿的介绍或者别的说明了，如果之后有空的话再做补充吧。最后附上一个扩展卡尔曼滤波器的例子，并附上 Matlab 代码。

文章目录

公式推导

状态方程

状态方程的例子可以套在绝大多数情况（话不能说满），所以这里也就没有举具体的例子，如果大家想参考相关的例子，可以看最下面的参考连接，推荐哔哩哔哩 Up主 Dr_Can 的视频。

在自动控制原理中，连续系统状态方程表示如下：
X ˙ = A X + B u Y = C X + D u \begin{aligned} \dot{X} &= AX+Bu\\ Y&=CX+Du \end{aligned} X˙Y​=AX+Bu=CX+Du​
其中 X X X 为状态变量， Y Y Y 为输出值或是待观测的变量， u u u 为输入， D D D 为输入对输出的直接影响，可以为 0 矩阵，所以上式也通常写为：

X ˙ = A X + B u Y = C X \begin{aligned} \dot{X} &= AX+Bu\\ Y&=CX \end{aligned} X˙Y​=AX+Bu=CX​

为了实际处理，我们需要将状态方程离散化，离散化后为：

X k = A k X k − 1 + B k u k − 1 Z k = H k X k \begin{aligned} X_k &= A_{k}X_{k-1}+B_ku_{k-1}\\ Z_k &= H_{k}X_{k} \end{aligned} Xk​Zk​​=Ak​Xk−1​+Bk​uk−1​=Hk​Xk​​

注意：这里的 A k , B k {A_k},{B_k} Ak​,Bk​ 与离散化之前的值并不相同，要根据实际情况进行离散化。

实际情况中，无论是系统本身，还是观测器都伴随有噪声的影响，这也是要进行卡尔曼滤波的原因，加入噪声后得到如下公式：

真实值：

X k = A k X k − 1 + B k u k − 1 + w k − 1 (1) \tag{1} X_k = A_{k}X_{k-1}+B_ku_{k-1} +w_{k-1} Xk​=Ak​Xk−1​+Bk​uk−1​+wk−1​(1)

观测值：

Z k = H k X k + V k (2) \tag{2} Z_k = H_{k}X_{k}+V_k Zk​=Hk​Xk​+Vk​(2)

其中

w k − 1 w_{k-1} wk−1​ 为系统的噪声，符合高斯分布 w k ∼ N ( 0 , Q k ) w_k \sim N(0,Q_k) wk​∼N(0,Qk​)

v k v_k vk​ 为测量噪声，符合高斯分布 v k ∼ N ( 0 , R k ) v_k \sim N(0,R_k) vk​∼N(0,Rk​)

预测值：

X ^ k − = A k X ^ k − 1 + B k u k (3) \tag{3} {\mathbf{\hat{X}}_k^-} = {A_k}{\mathbf{\hat{X}}_{k-1}} + {B_k}{u_k} X^k−​=Ak​X^k−1​+Bk​uk​(3)

注： 因为无法知道 w k w_{k} wk​ 的值，所以我们无法知道真实值 X k X_k Xk​ 的具体位置，但忽略噪声影响的预测值（先验估计值） X ^ k − {\mathbf{\hat{X}}_k^-} X^k−​ ，可以通过带入上一次的计算值（后验估计值） X ^ k − 1 {\hat{X}}_{k-1} X^k−1​得出。我们通过预测值，就得到了关于 真实值 X k X_k Xk​ 的高斯分布预测 真实值 X k ∼ N ( X ^ k − , P k − ) X_k\sim N({{\hat{X}}_k^-},P_k^-) Xk​∼N(X^k−​,Pk−​)

其中 P k − P_k^- Pk−​ 为先验估计的协方差矩阵
P k − = E ( e k − , e k − T ) e k − = ( X k − X ^ k − ) \begin{aligned} {P_k^-} &= E(e_k^-,e_k^{-T})\\ e{_k^-} &= (X_{k}-{\hat{X}_k^-})\\ \end{aligned} Pk−​ek−​​=E(ek−​,ek−T​)=(Xk​−X^k−​)​

先验估计误差 e k − e{_k^-} ek−​
e k − = X k − X ^ k − = A X k − 1 + B u k − 1 + w k − 1 − ( A X ^ k − 1 + B u k − 1 ) = A ( X k − 1 − X ^ k − 1 ) + w k − 1 = A e k − 1 + w k − 1 \begin{aligned} e{_k^-}&=X_{k}-{\hat{X}_k^-}\\ &= AX_{k-1}+Bu_{k-1}+w_{k-1}-(A\hat{X}_{k-1}+Bu_{k-1})\\ &= A(X_{k-1}-\hat{X}_{k-1})+w_{k-1}\\ &= Ae_{k-1}+w_{k-1} \end{aligned} ek−​​=Xk​−X^k−​=AXk−1​+Buk−1​+wk−1​−(AX^k−1​+Buk−1​)=A(Xk−1​−X^k−1​)+wk−1​=Aek−1​+wk−1​​
其中 e k − 1 − e^-_{k-1} ek−1−​ 为后验误差

先验估计误差的协方差矩阵 P k − {P_k^-} Pk−​：
P k − = E ( e k − , e k − T ) = E [ ( A e k − 1 + w k − 1 ) ( A e k − 1 + w k − 1 ) T ] = E [ ( A e k − 1 + w k − 1 ) ( e k − 1 T A T + w k − 1 T ) ] = E [ A e k − 1 e k − 1 T A T + A e k − 1 w k − 1 T + w k − 1 e k − 1 T A T + w k − 1 w k − 1 T ] = A E ( e k − 1 e k − 1 T ) A T + A E ( e k − 1 w k − 1 T ) + E ( w k − 1 e k − 1 T ) A T + E ( w k − 1 w k − 1 T ) \begin{aligned} {P_k^-}&= E(e_k^-,e_k^{-T})\\ &= E[(Ae_{k-1}+w_{k-1})(Ae_{k-1}+w_{k-1})^T]\\ &= E[(Ae_{k-1}+w_{k-1})({e^T_{k-1}}A^T+w^T_{k-1})]\\ &= E[Ae_{k-1}{e^T_{k-1}}A^T+Ae_{k-1}w^T_{k-1}+w_{k-1}{e^T_{k-1}}A^T+w_{k-1}w^T_{k-1}]\\ &= AE(e_{k-1}{e^T_{k-1}})A^T+AE(e_{k-1}w^T_{k-1})+E(w_{k-1}{e^T_{k-1}})A^T+E(w_{k-1}w^T_{k-1})\\ \end{aligned} Pk−​​=E(ek−​,ek−T​)=E[(Aek−1​+wk−1​)(Aek−1​+wk−1​)T]=E[(Aek−1​+wk−1​)(ek−1T​AT+wk−1T​)]=E[Aek−1​ek−1T​AT+Aek−1​wk−1T​+wk−1​ek−1T​AT+wk−1​wk−1T​]=AE(ek−1​ek−1T​)AT+AE(ek−1​wk−1T​)+E(wk−1​ek−1T​)AT+E(wk−1​wk−1T​)​
其中 由于 e k − 1 e_{k-1} ek−1​ 与 w k − 1 w_{k-1} wk−1​ 相互独立，所以 A E ( e k − 1 w k − 1 T ) AE(e_{k-1}w^T_{k-1}) AE(ek−1​wk−1T​)、 E ( w k − 1 e k − 1 T ) A T E(w_{k-1}{e^T_{k-1}})A^T E(wk−1​ek−1T​)AT 两项为 0 0 0 。 E ( w k − 1 w k − 1 T ) = Q k − 1 E(w_{k-1}w^T_{k-1}) = Q_{k-1} E(wk−1​wk−1T​)=Qk−1​ E ( e k − 1 e k − 1 T ) = P k − 1 E(e_{k-1}{e^T_{k-1}}) = P_{k-1} E(ek−1​ek−1T​)=Pk−1​ ，所以上式可简化为：
P k − = A P k − 1 A T + Q k − 1 (4) \tag{4} {P_k^-}= AP_{k-1}A^T+Q_{k-1} Pk−​=APk−1​AT+Qk−1​(4)
对于观测值 Z k = H k X k + V k Z_k = H_{k}X_{k}+V_k Zk​=Hk​Xk​+Vk​
Z k = H k X k + V k H k X k = Z k − V k X k = H k − 1 ( Z k − V k ) \begin{aligned} Z_k &= H_{k}X_{k}+V_k\\ H_{k}X_{k} &= Z_k-V_k\\ X_{k} &= {H_{k}^{-1}}(Z_k-V_k)\\ \end{aligned} Zk​Hk​Xk​Xk​​=Hk​Xk​+Vk​=Zk​−Vk​=Hk−1​(Zk​−Vk​)​
由于无法建模观测噪声 V k V_k Vk​ 的影响，所以
X m e a _ k = H k − 1 Z k X_{mea\_k} = {H_{k}^{-1}}Z_k Xmea_k​=Hk−1​Zk​

数据融合

至此，我们就知道了两个数据来源，一个是我们根据 公式 3 进行的预测值，一个是我们根据观测获得的测量值，这两个值都有误差，且误差都服从高斯分布，这就需要我们通过数据融合的思想，来获取更为精确的数据。

后验估计

采用数据融合的思想，新的预测数据 X ^ k \hat{X}_{k} X^k​ 由下式获得：
X ^ k = X ^ k − + G k ( X m e a _ k − X ^ k − ) = X ^ k − + G k ( H k − 1 Z k − X ^ k − ) 令 G k = K k H k = X ^ k − + K k H k ( H k − 1 Z k − X ^ k − ) = X ^ k − + K k ( Z k − H k X ^ k − ) \begin{aligned} {\hat{X}_{k}}&={\hat{X}_k^-}+{G_k}(X_{mea\_k}-{\hat{X}_k^-})\\ &={\hat{X}_k^-}+{G_k}({H_{k}^{-1}}Z_k-{\hat{X}_k^-})\\\\ &令 G_k = {K_k}{H_{k}}\\ &={\hat{X}_k^-}+{K_k}{H_{k}}({H_{k}^{-1}}Z_k-{\hat{X}_k^-})\\ &={\hat{X}_k^-}+{K_k}(Z_k-{H_{k}}{\hat{X}_k^-})\\ \end{aligned} X^k​​=X^k−​+Gk​(Xmea_k​−X^k−​)=X^k−​+Gk​(Hk−1​Zk​−X^k−​)令Gk​=Kk​Hk​=X^k−​+Kk​Hk​(Hk−1​Zk​−X^k−​)=X^k−​+Kk​(Zk​−Hk​X^k−​)​

X ^ k = X ^ k − + K k ( Z k − H k X ^ k − ) (5) \tag{5} {\hat{X}_{k}}={\hat{X}_k^-}+{K_k}(Z_k-{H_{k}}{\hat{X}_k^-})\\ X^k​=X^k−​+Kk​(Zk​−Hk​X^k−​)(5)

则Kalman Gain K k K_k Kk​ 的取值范围为：
K k ∈ [ 0 , H k − 1 ] w h e n : K k = 0 , X ^ k = X ^ k − w h e n : K k = H k − 1 , X ^ k = X m e a _ k \begin{aligned} &K_k\in[0,H{_k^{-1}}]\\ when:&K_k = 0,&\hat{X}_{k}&={\hat{X}_k^-}\\ when :&K_k = H{_k^{-1}},&\hat{X}_{k}&=X_{mea\_k} \end{aligned} when:when:​Kk​∈[0,Hk−1​]Kk​=0,Kk​=Hk−1​,​X^k​X^k​​=X^k−​=Xmea_k​​

这样就变成如下目标，寻找 K k K_k Kk​ 值，使得后验误差 X k − X ^ k X_k-\hat{X}_k Xk​−X^k​ 误差最小。
e k = X k − X ^ k e_k=X_k-\hat{X}_k ek​=Xk​−X^k​

后验误差的协方差矩阵

P k = E ( e , e T ) = [ σ e 1 2 σ e 1 e 2 σ e 2 e 1 σ e 2 2 ] P_k=E(e,e^T)= \begin{bmatrix} \sigma_{e_1}^2 & \sigma_{e_1e_2} \\ \sigma_{e_2e_1} & \sigma_{e_2}^2 \\ \end{bmatrix} Pk​=E(e,eT)=[σe1​2​σe2​e1​​​σe1​e2​​σe2​2​​]

希望误差最小，既 X ^ k \hat{X}_k X^k​ 越接近 X k X_k Xk​ ，既方差最小，既 P k P_k Pk​ 的 t r ( P k ) tr(P_k) tr(Pk​) 最小。
X k − X ^ k = X k − X ^ k − − K k ( Z k − H k X ^ k − ) = X k − X ^ k − − K k Z k + K k H k X ^ k − = X k − X ^ k − − K k ( H k X k + V k ) + K k H k X ^ k − = X k − X ^ k − − K k H k X k − K k V k + K k H k X ^ k − = ( X k − X ^ k − ) − K k H k ( X k − X ^ k − ) − K k V k = ( I − K k H k ) ( X k − X ^ k − ) − K k V k = ( I − K k H k ) e k − − K k V k \begin{aligned} X_k-\hat{X}_k&= X_k-{\hat{X}_k^-}-{K_k}({Z_k}-{H_k}{\hat{X}_k^-})\\ &= X_k-{\hat{X}_k^-}-{K_k}{Z_k}+{K_k}{H_k}{\hat{X}_k^-}\\ &= X_k-{\hat{X}_k^-}-{K_k}({H_k}{X_k}+{V_k})+{K_k}{H_k}{\hat{X}_k^-}\\ &= X_k-{\hat{X}_k^-}-{K_k}{H_k}{X_k}-{K_k}{V_k}+{K_k}{H_k}{\hat{X}_k^-}\\ &= (X_k-{\hat{X}_k^-})-{K_k}{H_k}({X_k}-{\hat{X}_k^-})-{K_k}{V_k}\\ &= (I-{K_k}{H_k})({X_k}-{\hat{X}_k^-})-{K_k}{V_k}\\ &= (I-{K_k}{H_k}){e_k^-}-{K_k}{V_k}\\ \end{aligned} Xk​−X^k​​=Xk​−X^k−​−Kk​(Zk​−Hk​X^k−​)=Xk​−X^k−​−Kk​Zk​+Kk​Hk​X^k−​=Xk​−X^k−​−Kk​(Hk​Xk​+Vk​)+Kk​Hk​X^k−​=Xk​−X^k−​−Kk​Hk​Xk​−Kk​Vk​+Kk​Hk​X^k−​=(Xk​−X^k−​)−Kk​Hk​(Xk​−X^k−​)−Kk​Vk​=(I−Kk​Hk​)(Xk​−X^k−​)−Kk​Vk​=(I−Kk​Hk​)ek−​−Kk​Vk​​

协方差矩阵：
P k = E ( e , e T ) = E ( ( X k − X ^ k ) ( X k − X ^ k ) T ) = E ( ( I − K k H k ) e k − − K k V k ) ( ( I − K k H k ) e k − − K k V k ) T ) = E ( ( I − K k H k ) e k − − K k V k ) ( e k − T ( I − K k H k ) T − V k T K k T ) T ) = E ( ( I − K k H k ) e k − e k − T ( I − K k H k ) T − ( I − K k H k ) e k − V k T K k T − K k V k e k − T ( I − K k H k ) T + K k V k V k T K k T ) = E ( ( I − K k H k ) e k − e k − T ( I − K k H k ) T ) − E ( ( I − K k H k ) e k − V k T K k T ) − E ( K k V k e k − T ( I − K k H k ) T ) + E ( K k V k V k T K k T ) \begin{aligned} P_k &= E(e,e^T)\\ &= E(({X_k}-{\hat{X}_k})({X_k}-{\hat{X}_k})^T)\\ &= E((I-{K_k}{H_k}){e_k^-}-{K_k}{V_k})((I-{K_k}{H_k}){e_k^-}-{K_k}{V_k})^T)\\ &= E((I-{K_k}{H_k}){e_k^-}-{K_k}{V_k})({{e_k^-}^T}(I-{K_k}{H_k})^T-{V_k^T}{K_k^T})^T)\\ &= E((I-{K_k}{H_k}){e_k^-}{{e_k^-}^T}(I-{K_k}{H_k})^T-(I-{K_k}{H_k}){e_k^-}{V_k^T}{K_k^T} -{K_k}{V_k}{{e_k^-}^T}(I-{K_k}{H_k})^T+{K_k}{V_k}{V_k^T}{K_k^T})\\ &= E((I-{K_k}{H_k}){e_k^-}{{e_k^-}^T}(I-{K_k}{H_k})^T) - E((I-{K_k}{H_k}){e_k^-}{V_k^T}{K_k^T}) - E({K_k}{V_k}{{e_k^-}^T}(I-{K_k}{H_k})^T) + E({K_k}{V_k}{V_k^T}{K_k^T})\\ \end{aligned} Pk​​=E(e,eT)=E((Xk​−X^k​)(Xk​−X^k​)T)=E((I−Kk​Hk​)ek−​−Kk​Vk​)((I−Kk​Hk​)ek−​−Kk​Vk​)T)=E((I−Kk​Hk​)ek−​−Kk​Vk​)(ek−​T(I−Kk​Hk​)T−VkT​KkT​)T)=E((I−Kk​Hk​)ek−​ek−​T(I−Kk​Hk​)T−(I−Kk​Hk​)ek−​VkT​KkT​−Kk​Vk​ek−​T(I−Kk​Hk​)T+Kk​Vk​VkT​KkT​)=E((I−Kk​Hk​)ek−​ek−​T(I−Kk​Hk​)T)−E((I−Kk​Hk​)ek−​VkT​KkT​)−E(Kk​Vk​ek−​T(I−Kk​Hk​)T)+E(Kk​Vk​VkT​KkT​)​
其中：
E ( ( I − K k H k ) e k − V k T K k T ) = ( I − K k H k ) E ( e k − V k T ) K k T E ( K k V k e k − T ( I − K k H k ) T ) = K k E ( V k e k − T ) ( I − K k H k ) T E((I-{K_k}{H_k}){e_k^-}{V_k^T}{K_k^T}) = (I-{K_k}{H_k})E({e_k^-}{V_k^T}){K_k^T}\\ E({K_k}{V_k}{{e_k^-}^T}(I-{K_k}{H_k})^T) ={K_k}E({V_k}{{e_k^-}^T})(I-{K_k}{H_k})^T E((I−Kk​Hk​)ek−​VkT​KkT​)=(I−Kk​Hk​)E(ek−​VkT​)KkT​E(Kk​Vk​ek−​T(I−Kk​Hk​)T)=Kk​E(Vk​ek−​T)(I−Kk​Hk​)T
在 E ( V k e k − T ) E({V_k}{{e_k^-}^T}) E(Vk​ek−​T) 中 V k 与 e k − T {V_k}与{{e_k^-}^T} Vk​与ek−​T 相互独立，故上面两个式子都为0.
P k = E ( e , e T ) = E ( ( I − K k H k ) e k − e k − T ( I − K k H k ) T ) + E ( K k V k V k T K k T ) = ( I − K k H k ) P k − ( I − K k H k ) T + K k R k K k T = ( P k − − K k H k P k − ) ( I − K k H k ) T + K k R k K k T = P k − − K k H k P k − − P k − H k T K k T + K k H k P k − H k T K k T + K k R k K k T \begin{aligned} P_k &= E(e,e^T)\\ &= E((I-{K_k}{H_k}){e_k^-}{{e_k^-}^T}(I-{K_k}{H_k})^T) + E({K_k}{V_k}{V_k^T}{K_k^T})\\ &= (I-{K_k}{H_k}){P_k^-}(I-{K_k}{H_k})^T + {K_k}{R_k}{K_k^T}\\ &= ({P_k^-}-{K_k}{H_k}{P_k^-})(I-{K_k}{H_k})^T + {K_k}{R_k}{K_k^T}\\ &= {P_k^-} - {K_k}{H_k}{P_k^-} - {P_k^-}{H_k^T}{K_k^T} + {K_k}{H_k}{P_k^-}{H_k^T}{K_k^T} + {K_k}{R_k}{K_k^T} \end{aligned} Pk​​=E(e,eT)=E((I−Kk​Hk​)ek−​ek−​T(I−Kk​Hk​)T)+E(Kk​Vk​VkT​KkT​)=(I−Kk​Hk​)Pk−​(I−Kk​Hk​)T+Kk​Rk​KkT​=(Pk−​−Kk​Hk​Pk−​)(I−Kk​Hk​)T+Kk​Rk​KkT​=Pk−​−Kk​Hk​Pk−​−Pk−​HkT​KkT​+Kk​Hk​Pk−​HkT​KkT​+Kk​Rk​KkT​​

协方差矩阵的迹

t r ( P k ) = t r ( P k − ) − t r ( K k H k P k − ) − t r ( P k − H k T K k T ) + t r ( K k H k P k − H k T K k T ) + t r ( K k R k K k T ) = t r ( P k − ) − 2 t r ( K k H k P k − ) + t r ( K k H k P k − H k T K k T ) + t r ( K k R k K k T ) 因为： t r ( A ) = t r ( A T ) ( ( P k − H k T ) K k T ) T = K k H k P k − T P k − 是对称矩阵 P k − = P k − T \begin{aligned} & tr(P_k) &&\\ =& tr({P_k^-}) - tr({K_k}{H_k}{P_k^-}) - tr({P_k^-}{H_k^T}{K_k^T})+ tr({K_k}{H_k}{P_k^-}{H_k^T}{K_k^T}) + tr({K_k}{R_k}{K_k^T})\\ =& tr({P_k^-}) - 2tr({K_k}{H_k}{P_k^-}) + tr({K_k}{H_k}{P_k^-}{H_k^T}{K_k^T}) + tr({K_k}{R_k}{K_k^T})\\ \end{aligned} \begin{aligned} &因为：\\ &tr(A) = tr(A^T)\\ &{(({P_k^-}{H_k^T}){K_k^T})^T}={K_k}{H_k}{{P_k^-}^T}\\ &{P_k^-}是对称矩阵{P_k^-}={{P_k^-}^T} \end{aligned} ==​tr(Pk​)tr(Pk−​)−tr(Kk​Hk​Pk−​)−tr(Pk−​HkT​KkT​)+tr(Kk​Hk​Pk−​HkT​KkT​)+tr(Kk​Rk​KkT​)tr(Pk−​)−2tr(Kk​Hk​Pk−​)+tr(Kk​Hk​Pk−​HkT​KkT​)+tr(Kk​Rk​KkT​)​​因为：tr(A)=tr(AT)((Pk−​HkT​)KkT​)T=Kk​Hk​Pk−​TPk−​是对称矩阵Pk−​=Pk−​T​

求 K k K_k Kk​ 的最小值，即 t r ( P k ) tr(P_k) tr(Pk​) 对 K k K_k Kk​ 求导：
d ( t r ( P k ) ) d ( K k ) = 0 − 2 ( H k P k − ) T + 2 K k H k P k − H k T + 2 K k R k 因为： d ( t r ( A B ) ) d ( A ) = B T d ( t r ( A B A T ) ) d ( A ) = 2 A B \begin{aligned} &\frac{d(tr(P_k))}{d(K_k)}=0 - 2({H_k}{{P_k^-}})^T+2{K_k}{H_k}{P_k^-}{H_k^T}+2{K_k}{R_k}&&&\\ \end{aligned} \begin{aligned} 因为：&\\ &\frac{d(tr(AB))}{d(A)}=B^T\\ &\frac{d(tr(AB{A^T}))}{d(A)}=2AB\\ \end{aligned}\\ ​d(Kk​)d(tr(Pk​))​=0−2(Hk​Pk−​)T+2Kk​Hk​Pk−​HkT​+2Kk​Rk​​​​​因为：​d(A)d(tr(AB))​=BTd(A)d(tr(ABAT))​=2AB​
令 d ( t r ( P k ) ) d ( K k ) = 0 \frac{d(tr(P_k))}{d(K_k)}=0 d(Kk​)d(tr(Pk​))​=0
− 2 ( H k P k − ) T + 2 K k H k P k − H k T + 2 K k R k = 0 K k H k P k − H k T + K k R k = ( H k P k − ) T K k ( H k P k − H k T + R k ) = P k − T H k T \begin{aligned} -2({H_k}{{P_k^-}})^T+2{K_k}{H_k}{P_k^-}{H_k^T}+2{K_k}{R_k}&=0&&&&&&&&&&\\ {K_k}{H_k}{P_k^-}{H_k^T}+{K_k}{R_k}&=({H_k}{{P_k^-}})^T\\ {K_k}({H_k}{P_k^-}{H_k^T}+{R_k})&={{P_k^-}^T}{H_k^T}\\ \end{aligned} −2(Hk​Pk−​)T+2Kk​Hk​Pk−​HkT​+2Kk​Rk​Kk​Hk​Pk−​HkT​+Kk​Rk​Kk​(Hk​Pk−​HkT​+Rk​)​=0=(Hk​Pk−​)T=Pk−​THkT​​

卡尔曼增益

K k = P k − T H k T H k P k − H k T + R k (6) \tag{6} {K_k}=\frac{{{P_k^-}^T}{H_k^T}}{{H_k}{P_k^-}{H_k^T}+{R_k}}\\ Kk​=Hk​Pk−​HkT​+Rk​Pk−​THkT​​(6)

同时：
P k = P k − − K k H k P k − − P k − H k T K k T + K k H k P k − H k T K k T + K k R k K k T = P k − − K k H k P k − − P k − H k T K k T + K k ( H k P k − H k T + K k R k ) K k T = P k − − K k H k P k − − P k − H k T K k T + P k − H k T K k T = P k − − K k H k P k − = ( I − K k H k ) P k − \begin{aligned} P_k &= {P_k^-} - {K_k}{H_k}{P_k^-} - {P_k^-}{H_k^T}{K_k^T} + {K_k}{H_k}{P_k^-}{H_k^T}{K_k^T} + {K_k}{R_k}{K_k^T}\\ &= {P_k^-} - {K_k}{H_k}{P_k^-} - {P_k^-}{H_k^T}{K_k^T} + {K_k}({H_k}{P_k^-}{H_k^T} + {K_k}{R_k}){K_k^T}\\ &= {P_k^-} - {K_k}{H_k}{P_k^-} - {P_k^-}{H_k^T}{K_k^T} + {P_k^-}{H_k^T}{K_k^T}\\ &= {P_k^-} - {K_k}{H_k}{P_k^-}\\ &= (I - {K_k}{H_k}){P_k^-}\\ \end{aligned} Pk​​=Pk−​−Kk​Hk​Pk−​−Pk−​HkT​KkT​+Kk​Hk​Pk−​HkT​KkT​+Kk​Rk​KkT​=Pk−​−Kk​Hk​Pk−​−Pk−​HkT​KkT​+Kk​(Hk​Pk−​HkT​+Kk​Rk​)KkT​=Pk−​−Kk​Hk​Pk−​−Pk−​HkT​KkT​+Pk−​HkT​KkT​=Pk−​−Kk​Hk​Pk−​=(I−Kk​Hk​)Pk−​​

P k = ( I − K k H k ) P k − (7) \tag{7} P_k = (I - {K_k}{H_k}){P_k^-}\\ Pk​=(I−Kk​Hk​)Pk−​(7)

至此，公式推导结束。

卡尔曼滤波器的使用

  1. 计算先验估计值
    X ^ k − = A k X ^ k − 1 + B k u k {\mathbf{\hat{X}}_k^-} = {A_k}{\mathbf{\hat{X}}_{k-1}} + {B_k}{u_k} X^k−​=Ak​X^k−1​+Bk​uk​

  2. 更新先验误差的协方差矩阵
    P k − = A P k − 1 A T + Q k − 1 {P_k^-}= AP_{k-1}A^T+Q_{k-1} Pk−​=APk−1​AT+Qk−1​

  3. 计算Kalman Gain
    K k = P k − T H k T H k P k − H k T + R k {K_k}=\frac{{{P_k^-}^T}{H_k^T}}{{H_k}{P_k^-}{H_k^T}+{R_k}}\\ Kk​=Hk​Pk−​HkT​+Rk​Pk−​THkT​​

  4. 计算后验估计
    X ^ k = X ^ k − + K k ( Z k − H k X ^ k − ) {\hat{X}_{k}}={\hat{X}_k^-}+{K_k}(Z_k-{H_{k}}{\hat{X}_k^-}) X^k​=X^k−​+Kk​(Zk​−Hk​X^k−​)

  5. 更新误差协方差矩阵

P k = ( I − K k H k ) P k − P_k = (I - {K_k}{H_k}){P_k^-} Pk​=(I−Kk​Hk​)Pk−​

参考

【1】【卡尔曼滤波器】3_卡尔曼增益超详细数学推导 ～全网最完整_哔哩哔哩_bilibili

【2】通过简单直观的推导理解卡尔曼基础)Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation_tuszhangs的博客-CSDN博客

【3】Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation (Lecture Note | IEEE Journals & Magazine | IEEE Xplore )

【4】轻松理解卡尔曼滤波 - 知乎

【5】How a Kalman filter works, in pictures | Bzarg

【6】kalman滤波理解一：理论框架_还差得远呢的博客-CSDN博客

【7】probability - Is the product of two Gaussian random variables also a Gaussian? - Mathematics Stack Exchange

例子

这是一个基于扩展卡尔曼滤波器的例子
在这里插入图片描述

clear
clc
%初始参数
%状态函数：
[ x_k v_xk y_k v_yk]'
X = [0 10 200 0]';
t = 10;
T = 0.1;
m = 1;
kx = 0.01;
ky = 0.05;
g = -9.8;
Status = [T,g,m,kx,ky];
I = eye(4);

H = zeros(2,4);


% 初始的误差协方差矩阵
P_k1  = zeros(4,4);
% 噪声
Q = zeros(4,4);
Q(2,2) = 5;
Q(4,4) = 5;
R = eye(2);
R(1,1) = 0.0004;
R(2,2) = 3;
P_k1,Q,R
X_real = X;
X_real1 = X;
X_head1 = X;
X_headp = zeros(4,1);
X_head = zeros(4,1);


XY = zeros(t/T,4);
ZZ = zeros(t/T,2);

%生成 A，H 矩阵
A = [1          T               0       0; 
     0   1-2*T/m*kx*X(2)        0       0; 
     0          0               1       T;
     0          0               0   1+2*T/m*ky*X(4)];
H = zeros(2,4);

%迭代计算
rng(10);
for i = 1: t/T
    % 构造真实值
    X_real = CreatRealDatas(X_real1, Status, Q);
    % 构造观测值
    Zk = CreatObserveDatas(X_real, R);
    % 计算先验值
    X_headp = CalculatePriorValue(X_head1, Status);
    % 更新 A H 矩阵
    [A, H] = UpdateAHmatrix(X_head1, Status);
    % 误差协方差矩阵 Pk 的先验值
    Pkp = A*P_k1*A' + Q;
    % 计算 Kalman Gain
    Kk = Pkp*H'*(H*Pkp*H'+ R)^-1;
    % 计算 后验估计
    

    ZZ_a = atan(X_headp(1)/X_headp(3));
    ZZ_r = sqrt(X_headp(1)^2 + X_headp(3)^2);
    abc = [ZZ_a,ZZ_r]';
    

    % X_head = X_headp + Kk*(Zk - H*X_headp);
    X_head = X_headp + Kk*(Zk - abc);
    % 更新误差的协方差矩阵
    Pk = (I - Kk*H)*Pkp;
%数据更新
   
    X_real1 = X_real;
    X_head1 = X_head;
    P_k1 = Pk;
    
    XY(i,:) = X_real;
    Xh(i,:) = X_head;
    ZZ(i,:) = Zk;
end

%绘制图像
figure(1)
hold on
ZZ2 = [ZZ(:,2).*sin(ZZ(:,1)),ZZ(:,2).*cos(ZZ(:,1))];
plot(XY(:,1),XY(:,3),'r');
plot(ZZ2(:,1),ZZ2(:,2),'*');
plot(Xh(:,1),Xh(:,3),'g');

figure(2)
hold on
plot(XY(:,2),'r')
plot(XY(:,4),'b')

函数创建

  1. 构造真实值
function X_real = CreatRealDatas(X_real1, Status, Q)
    X_k1 = X_real1(1); V_xk1 = X_real1(2); Y_k1 = X_real1(3); V_yk1 = X_real1(4);
    T = Status(1); g = Status(2); m = Status(3); kx =Status(4); ky = Status(5);
    
    X_k = X_k1 + T*V_xk1;
    if V_xk1 >= 0
        V_xk = V_xk1 - T/m*kx * V_xk1*V_xk1 + Q(2,2)^0.5*randn(1)*T;
    else
        V_xk = V_xk1 + T/m*kx * V_xk1*V_xk1 + Q(2,2)^0.5*randn(1)*T;
    end
    
    Y_k = Y_k1 + T*V_yk1;
    if V_yk1 >= 0
        V_yk = V_yk1 + T*g - T/m*ky * V_yk1*V_yk1  + Q(4,4)^0.5*randn(1)*T;
    else
        V_yk = V_yk1 + T*g + T/m*ky * V_yk1*V_yk1  + Q(4,4)^0.5*randn(1)*T;
    end
    X_real = [X_k V_xk Y_k V_yk]';
end
  1. 构造观测值
function Zk = CreatObserveDatas(X_real, R)

    X_k = X_real(1); Y_k = X_real(3);
 
    Z_a = atan(X_k/Y_k) + R(1,1)^0.5*randn(1);
    Z_r = sqrt(X_k^2 + Y_k^2) + R(2,2)^0.5*randn(1);
    Zk = [Z_a;Z_r];
end
  1. 计算先验值
function X_headp = CalculatePriorValue(X_head1, Status)

    T = Status(1); g = Status(2); m = Status(3); kx =Status(4); ky = Status(5);
    
    X_k = X_head1(1) + T*X_head1(2);
    if X_head1(2) >= 0
        V_xk = X_head1(2) - T/m*kx * X_head1(2)*X_head1(2);
    else
        V_xk = X_head1(2) + T/m*kx * X_head1(2)*X_head1(2);
    end
    
    Y_k = X_head1(3) + T*X_head1(4);
    if X_head1(4) >= 0
        V_yk = X_head1(4) + T*g - T/m*ky * X_head1(4)*X_head1(4);
    else
        V_yk = X_head1(4) + T*g + T/m*ky * X_head1(4)*X_head1(4);
    end
    X_headp = [X_k V_xk Y_k V_yk]';
end
  1. 更新 A，H 矩阵
function [A, H] = UpdateAHmatrix(X_head1, Status)
    
    T = Status(1); g = Status(2); m = Status(3); kx =Status(4); ky = Status(5);
    
    A = zeros(4);
    
    A(1,1) = 1;
    A(1,2) = T;
    A(2,2) = 1-2*T/m*kx*X_head1(2);
    A(3,3) = 1;
    A(3,4) = T;
    A(4,4) = 1+2*T/m*ky*X_head1(4);
    
    H = zeros(2,4);
    
    H(1,1) = X_head1(3)/(X_head1(1)^2 + X_head1(3)^2);
    H(1,3) = X_head1(1)/(X_head1(1)^2 + X_head1(3)^2);
    H(2,1) = X_head1(1)/sqrt(X_head1(1)^2 + X_head1(3)^2);
    H(2,3) = X_head1(3)/sqrt(X_head1(1)^2 + X_head1(3)^2);
end

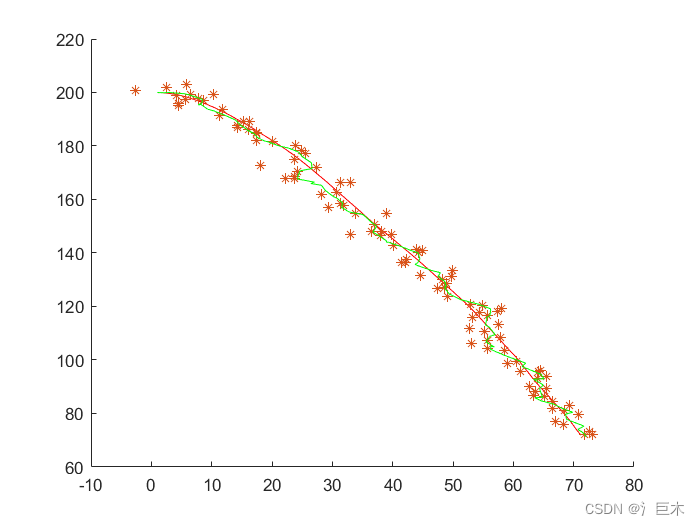
结果

红色 为真实值
* 为观测值
绿色 为滤波后的输出值。
在这里插入图片描述

氵巨木
关注
  • 1
    点赞
  • 踩
  • 2
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
专栏目录
Kalman Filter 公式推导过程
12-12
kalman filter 公式推导过程笔记；英文；BLUE:best&linear&unbiased&estimate.
kalman filter 卡尔曼滤波器讲解
04-03
卡尔曼滤波器是高斯线性滤波器，整个推导过程设计概率和矩阵知识比较多，文档内有详细推导过程（公式、概念都给出了参考链接），花上一天时间搞定卡尔曼滤波器妥妥的！
kalman filter 卡尔曼滤波 公式推导
D_turtle的博客
05-24 982
Kalman filter 一个线性时不变系统如下： xk+1=Axk+Buk+wkyk=Cxk+vkxk+1=Axk+Buk+wkyk=Cxk+vk x_{k+1} = Ax_k+Bu_k+w_k\\ y_k = Cx_k+v_k 其中，wkwkw_k是process noise, wk∈ℝnwk∈Rnw_k\in\mathbb{R}^n, wk∼(0,Q)wk∼N(0,Q)w_k\...
Kalman Filter卡尔曼滤波公式推导和视频行人跟踪应用
Hi
04-26 1097
Kalman Filter卡尔曼滤波公式推导和视频行人跟踪应用 随着传感技术、机器人、自动驾驶以及航空航天等技术的不断发展，对控制系统的精度及稳定性的要求也越来越高。卡尔曼滤波作为一种状态最优估计的方法，其应用也越来越普遍，如在无人机、机器人等领域均得到了广泛应用。 公式推导 1.递归算法了解 参考视频：【卡尔曼滤波器】1_递归算法_Recursive Processing_哔哩哔哩_bilibili 2.数学基础_数据融合_协方差矩阵_状态空间方程_观测器问题 参考视频：【卡尔曼滤波器】2_数
卡尔曼滤波（Kalman filter）公式推导详细版
davidsmith8的博客
09-16 3642
卡尔曼滤波（Kalman filter）公式推导详细版 记得很早的时候，我曾经手工推导过卡尔曼滤波，但是之前的已经大多记不起来了。今天帮着老师整理PPT的时候，老师让我补充完相应的推导相关的内容。所以今天就借着这个机会一并写一个卡尔曼滤波的公式的推导的博客。现在csdn上关于卡尔曼滤波的的推导的博客已经很多了，但是对于我这个入门小白来说，我还是觉得大神们的推导中间都省略了若干步骤，不够详细。所以...
卡尔曼滤波器Kalman Filter公式推导
LonlyForever的博客
11-19 421
卡尔曼滤波器Kalman Filter公式推导引言预测与校正预测:x^n−1∣n−1→x^n∣n−1\hat{\mathrm{x}}_{\mathrm{n}-1 \mid \mathrm{n}-1} \rightarrow \hat{\mathrm{x}}_{\mathrm{n} \mid \mathrm{n}-1}x^n−1∣n−1​→x^n∣n−1​校正：x^n∣n−1→x^n∣n\hat{\mathrm{x}}_{\mathrm{n} \mid \mathrm{n}-1} \rightarrow \h
卡尔曼滤波 (Kalman Filter) 公式推导
Frankgoogle的博客
08-14 920
Kalman Filter 本文简单介绍了卡尔曼滤波(Kalman Filter)的基本原理以及我对卡尔曼滤波的一些理解。 首先谈一下我的一点点理解 卡尔曼滤波是目前应用很广泛的一种滤波方法，最早由Kalman老先生在1960年提出，网上可以找到原文。这种方法最开始用在航天领域，作为轨道矫正的一种方法，有很好的效果。 卡尔曼滤波的方法的核心思想，就是用另一个测量空间的观测值去纠正当前空间对被测量的...
Kalman Filter 公式及推导
xajh_wk的博客
03-15 1770
1.介绍卡尔曼滤波的本质是参数化的贝叶斯模型，通过对下一时刻系统的初步状态估计（即状态的先验估计）以及测量得出的反馈相结合，最终得到该时刻较为准确的的状态估计（即状态的后验估计）。其核心思想即为预测+测量反馈。 Kalman fliter是线性滤波器 2.经典的5个公式：状态预测 “小帽子”表示估计，“-”表示用上一时刻的量估计而来的，F是状态转移矩阵，表示怎么由上一状态量怎么推测当前时刻状态；B...
卡尔曼滤波(kalman filter)超详细推导
littlefrogyq的博客
07-23 1710
1. 概率论相关知识 这一节主要叙述概率论的一些相关基础知识，包括全概率公式、贝叶斯公式、协方差矩阵、二维高斯分布等等，对这些熟悉的可以直接跳到第二节 1.1 全概率公式与贝叶斯公式 1.2 协方差矩阵 1.3 二维高斯分布 2. 贝叶斯(Bayes)滤波 卡尔曼滤波是基于贝叶斯滤波的一种改进，这里先说明一下贝叶斯滤波的相关原理。 2.1 变量定义 运动过程一般需要用到的变量主要有3个： xi\boldsymbol x_ixi​表示iii时刻的状态。比如在运动的机器人中，表示机器人当前的位姿 zi\bold
卡尔曼滤波（Kalman Filter）
qq_39645262的博客
02-06 1145
卡尔曼滤波算法作为一个在存在不确定性的情况下对系统状态进行估计和预测的强大工具，被广泛应用于诸如目标跟踪、导航和控制等场景。
卡尔曼滤波(Kalman Filter)概念介绍及详细公式推导
热门推荐
泽渊的博客
05-29 1万+
卡尔曼滤波（Kalman filter）是一种高效率的递归滤波器（自回归滤波器），它能够从一系列的不完全及包含噪声的测量中，估计动态系统的状态。卡尔曼滤波会根据各测量量在不同时间下的值，考虑各时间下的联合分布，再产生对未知变数的估计，因此会比只以单一测量量为基础的估计方式要准。卡尔曼滤波得名自主要贡献者之一的鲁道夫·卡尔曼。​ 卡尔曼滤波的算法是二步骤的程序。
卡尔曼滤波（Kalman Filter）原理与公式推导.pdf
12-23
卡尔曼滤波（Kalman Filter）原理与公式推导.pdf
卡尔曼滤波Kalman Filter
01-06
年少不知记笔记，老来方恨看不懂……本文从三方面进行，首先是卡尔曼滤波的思想，然后对卡尔曼滤波进行公式推导，最后是对卡尔曼滤波进行总结。 核心思想 取自知乎Kent Zeng的回答：点击链接，我对他的回答进行了...
kalman卡尔曼滤波.7z
12-24
最后，`An Introduction to the Kalman Filter.pdf`是2004年的英文文章，它详尽地介绍了卡尔曼滤波的基本理论和实际应用。这篇文章可能包括了滤波器的数学基础，如状态空间模型、贝叶斯估计、随机过程等，并提供了...
36. Adam 算法详解
qq_41238579的博客
07-10 961
Adam（Adaptive Moment Estimation）是一种结合动量法和自适应学习率的优化算法，自2014年提出以来，迅速成为深度学习中最流行和常用的优化算法之一。Adam算法的核心思想是利用梯度的一阶动量和二阶动量来动态调整学习率，既保持了动量法的优点，又结合了RMSProp的自适应学习率特性。
函数模板与类模板
程序员_小兵
07-12 1546
/交换int数据a = b;b = temp;//交换char数据a = b;b = temp;//问题：如果我要交换double类型数据，那么还需要些一个double类型数据交换的函数//繁琐，写的函数越多，当交换逻辑发生变化的时候，所有的函数都需要修改，无形当中增加了代码的维护难度//如果能把类型作为参数传递进来就好了，传递int就是Int类型交换，传递char就是char类型交换//我们有一种技术，可以实现类型的参数化---函数模板。
2024C++信息素养大赛-算法创意实践挑战_复赛真题（广东省）题目+参考答案和详细解析
最新发布
m0_74586426的博客
07-12 704
2024C++信息素养大赛-算法创意实践挑战_复赛真题（广东省）题目+参考答案和详细解析
【排序 - 堆排序】
2302_80393814的博客
07-10 548
堆排序利用堆这种数据结构的特性，通过构建最大堆和不断调整堆的过程来实现排序。它的时间复杂度稳定在 O(n log n)，并且适用于大数据量的排序需求。通过本文，我们深入了解了堆排序的原理和实现方式，并通过C语言代码展示了如何实现堆排序算法。对于理解高效排序算法和算法设计有着重要的帮助。
可信集合卡尔曼公式推导
04-18
可信集合卡尔曼滤波（Covariance Intersection Kalman Filter）是一种用于融合多个传感器数据的滤波算法。它通过将不同传感器的测量结果进行融合，得到更准确和可信的估计值。 卡尔曼滤波是一种递归滤波算法，它...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值