树的定义
在计算机科学中,树(tree)是一种抽象数据类型(ADT),用来模拟具有树状结构性质的数据集合。它是由n(n>=1)个有限节点组成的一个具有层状关系的集合。把它叫“树”是因为它看起来像一颗倒挂的树,也就是说它是根朝上而叶朝下的。
树的相关术语
- 节点的度:一个节点含有的子树的个数称为该节点的度。
- 树的度:一棵树中,最大的节点的度称为树的度。
- 叶子结点:没有子节点的节点。
- 父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点。
- 节点的层次:从根开始定义起,根为第一层,根的子节点为第二层,以此类推。
- 树的高度或深度:树中节点的最大层次。
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟。
- 节点的祖先:从根到该节点所经分支上的所有节点。
- 子孙:以某一节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)颗互不相交的树的集合称为森林。
- 二叉树:任意节点的子节点个数不大于2。且子节点的顺序不能变。
- 满二叉树:如果一颗二叉树的节点要么有两个孩子节点要么是叶子结点,则为满二叉树。
- 完全二叉树:若设二叉树的深度为h,除第h层外,其他各层的节点数都达到最大个数,第h层所有的节点都连续集中在最左边,这就是完全二叉树。 (满二叉树是特殊的完全二叉树)。
二叉树的5个性质
- 二叉树第K层最多有 2k−1 个节点。
- 二叉树有K层节点最多为 2k−1 。
- 二叉树的叶子结点和度数为2的节点关系:N0 = N2+1(N0代表叶子节点个数,N2代表所有度数为2的节点个数)。
- 完全二叉树总结点个数为N,则层数为 [log2n]+1 。
- 如果有一颗有n个节点的完全二叉树的节点按层次序编号,对任一层的节点i(1<=i<=n)有
1.如果i=1 ,则节点是二叉树的根,无双亲;如果i>1,则其双亲节点为[i/2],向下取整。
2.如果2i>n那么节点i没有左孩子,否则其左孩子为2i。
3.如果2i+1>n那么节点没有右孩子,否则右孩子为2i+1。
树的存储
1.双亲表示法
假设以一组连续空间存储树的节点,同时在每个节点中,附设一个指示其双亲节点在数组中位置的元素。
也就是说每个节点不仅要知道自己是谁之外还要知道自己的父节点在哪。
结构特点如下:
| data | parent |
|---|
双亲表示法的结构定义代码:
/*树的双亲表示法节点结构定义*/
#define MAXSIZE 100
typedef int ElemType; //树结点的数据类型,可以在这儿进行更改
typedef struct PTNode //结点结构
{
ElemType data; //结点数据
int parent; //双亲位置
}PTNode;
typedef struct
{
PTNode nodes[MAXSIZE]; //结点数组
int position; //根的位置
int n; //节点数
}PTree;优缺点
查找双亲很方便,但是查找子节点比较麻烦,需要遍历全树。
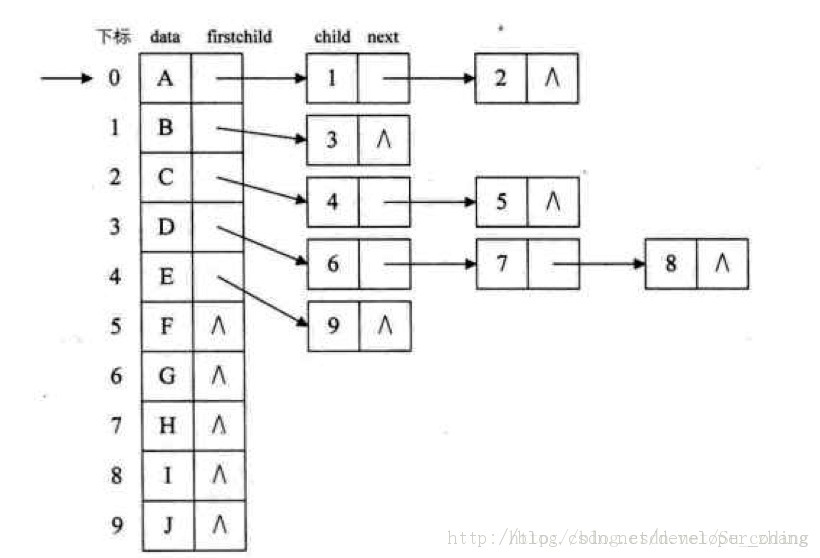
2.孩子表示法
与双亲表示法恰恰相反,双亲节点记录自己的孩子节点,获取最大的树的度。
从图中可以看出这张图片表示的树的最大度为3。
孩子表示法的结构定义代码:
#define MAXSIZE 100
#define char ElemType
typedef struct Cnode //孩子结点
{
ElemType child;
struct Cnode* next;
}*Cnode;
typedef struct
{
ElemType data;
int parent; //双亲的位置域
Cnode firstchild; //孩子的链表头指针
}PTNode;
typedef struct //树结构
{
PTNode node[MAXSIZE];
int count; //节点个数
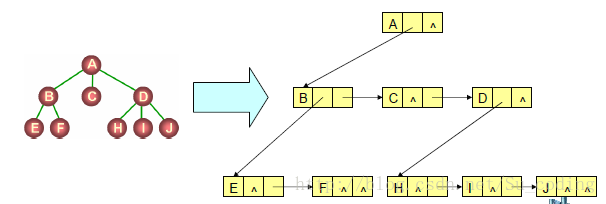
}CTree;3.孩子兄弟表示法
任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此,我们设置两个指针,分别指向该结点的第一个孩子和此结点的右兄弟。
结点结构图如下:
| data | firstchild | rightbrother |
|---|
孩子兄弟表示法示例图:
孩子兄弟表示法的结构定义代码:
typedef struct TreeNode
{
ElemType data;
struct TreeNode* firstchild;
struct TreeNode* rightbrother;
}TreeNode,*TreeNode;





















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








