机器学习
在应用机器学习算法时,我们通常采用梯度下降法来对采用的算法进行训练。其实,常用的梯度下降法还具体包含有三种不同的形式,它们也各自有着不同的优缺点。
下面我们以线性回归算法来对三种梯度下降法进行比较。
一般线性回归函数的假设函数为:
hθ=∑nj=0θjxjhθ=∑j=0nθjxj
对应的能量函数(损失函数)形式为:
Jtrain(θ)=1/(2m)∑mi=1(hθ(x(i))−y(i))2Jtrain(θ)=1/(2m)∑i=1m(hθ(x(i))−y(i))2
下图为一个二维参数(θ0θ0和θ1θ1)组对应能量函数的可视化图:

1. 批量梯度下降法BGD
批量梯度下降法(Batch Gradient Descent,简称BGD)是梯度下降法最原始的形式,它的具体思路是在更新每一参数时都使用所有的样本来进行更新,其数学形式如下:
(1) 对上述的能量函数求偏导:
(2) 由于是最小化风险函数,所以按照每个参数θθ的梯度负方向来更新每个θθ:
具体的伪代码形式为:
repeat{
(for every j=0, ... , n)
}
从上面公式可以注意到,它得到的是一个全局最优解,但是每迭代一步,都要用到训练集所有的数据,如果样本数目mm很大,那么可想而知这种方法的迭代速度!所以,这就引入了另外一种方法,随机梯度下降。
优点:全局最优解;易于并行实现;
缺点:当样本数目很多时,训练过程会很慢。
从迭代的次数上来看,BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下:

2. 随机梯度下降法SGD
由于批量梯度下降法在更新每一个参数时,都需要所有的训练样本,所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法(Stochastic Gradient Descent,简称SGD)正是为了解决批量梯度下降法这一弊端而提出的。
将上面的能量函数写为如下形式:
利用每个样本的损失函数对θθ求偏导得到对应的梯度,来更新θθ:
具体的伪代码形式为:
1. Randomly shuffle dataset;
2. repeat{
for i=1, ... , mm{
(for j=0, ... , nn)
}
}
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将theta迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
优点:训练速度快;
缺点:准确度下降,并不是全局最优;不易于并行实现。
从迭代的次数上来看,SGD迭代的次数较多,在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下:

3. 小批量梯度下降法MBGD
有上述的两种梯度下降法可以看出,其各自均有优缺点,那么能不能在两种方法的性能之间取得一个折衷呢?即,算法的训练过程比较快,而且也要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初衷。
MBGD在每次更新参数时使用b个样本(b一般为10),其具体的伪代码形式为:
Say b=10, m=1000.
Repeat{
for i=1, 11, 21, 31, ... , 991{

(for every j=0, ... , nn)
}
}
如果把梯度下降法想象成一个小球从山坡到山谷的过程,那么前面几篇文章的小球是这样移动的:从A点开始,计算当前A点的坡度,沿着坡度最大的方向走一段路,停下到B。在B点再看一看周围坡度最大的地方,沿着这个坡度方向走一段路,再停下。确切的来说,这并不像一个球,更像是一个正在下山的盲人,每走一步都要停下来,用拐杖来来探探四周的路,再走一步停下来,周而复始,直到走到山谷。而一个真正的小球要比这聪明多了,从A点滚动到B点的时候,小球带有一定的初速度,在当前初速度下继续加速下降,小球会越滚越快,更快的奔向谷底。momentum 动量法就是模拟这一过程来加速神经网络的优化的。
上图直观的解释了动量法的全部内容。
A为起始点,首先计算A点的梯度∇a∇a ,然后下降到B点,
θθ 为参数 αα 为学习率。
到了B点需要加上A点的梯度,这里梯度需要有一个衰减值 γγ ,推荐取0.9。这样的做法可以让早期的梯度对当前梯度的影响越来越小,如果没有衰减值,模型往往会震荡难以收敛,甚至发散。所以B点的参数更新公式是这样的:
其中 vt−1vt−1 表示之前所有步骤所累积的动量和。
这样一步一步下去,带着初速度的小球就会极速的奔向谷底。
2.Nesterov accelerated gradient(NAG)
Momentum改进自SGD算法,让每一次的参数更新方向不仅仅取决于当前位置的梯度,还受到上一次参数更新方向的影响:
公式1,Momentum的数学形式
其中,







所以Momentum的想法很简单,就是多更新一部分上一次迭代的更新量,来平滑这一次迭代的梯度。从物理的角度上解释,就像是一个小球滚落的时候会受到自身历史动量的影响,所以才叫动量(Momentum)算法。这样做直接的效果就是使得梯度下降的的时候转弯掉头的幅度不那么大了,于是就能够更加平稳、快速地冲向局部最小点:

图片引自《 An overview of gradient descent optimization algorithms》
然后NAG就对Momentum说:“既然我都知道我这一次一定会走


公式2,NAG的原始形式
跟上面Momentum公式的唯一区别在于,梯度不是根据当前参数位置

对于这个改动,很多文章给出的解释是,能够让算法提前看到前方的地形梯度,如果前面的梯度比当前位置的梯度大,那我就可以把步子迈得比原来大一些,如果前面的梯度比现在的梯度小,那我就可以把步子迈得小一些。这个大一些、小一些,都是相对于原来不看前方梯度、只看当前位置梯度的情况来说的。
为了从另一个角度更加深入地理解这个算法,我们可以对NAG原来的更新公式进行变换,得到这样的等效形式(具体推导过程放在最后啦):

公式3,NAG的等效形式
这个NAG的等效形式与Momentum的区别在于,本次更新方向多加了一个![\beta[g(\theta_{i-1}) - g(\theta_{i-2})]](http://image100.360doc.com/DownloadImg/2016/10/1008/81923986_17)
3:AdaGrad
如果我们希望根据每个参数去调节学习率,那么AdaGrad恰好解决了这个问题。AdaGrad算法根据每个参数过去的更新历史来决定现在的更新学习率。AdaGrad会记录之前每一步更新值的平方,通过将这些累加起来来调节每一步学习率的大小。这样一来,对于那些频繁更新的参数,学习率会比较小;而对于那些不频繁更新的参数,学习率会比较大。从这个角度看,AdaGrad很适合比较稀疏的数据。更新公式如下:
G=G+[g(param)]^2
param=param-lr*g(param)/sqrt(G+epsilon)
其中epsilon是一个极小值,为了数值稳定。AdaGrad的一个优点是它可以避免手动去调节学习率,并且在很多时候,只要初始化学习率为0.01即可,然后可以放任不管。但是,一个明显的缺点是随着更新步骤的增多,学习率将会一直减小直至接近于0,这样就会导致网络更新停滞。
4:RMSProp
RMSProp是为了解决算法3的学习率消失问题,通过在历史更新与梯度平方之间设置一定的比例。其更新公式如下:
G=0.9*G+0.1*[g(param)]^2
param=param-lr*g(param)/sqrt(G+epsilon)
RMSProp与接下来要讨论的算法5几乎是同时提出的。
5:AdaDelta
AdaDelta也是为了解决AdaGrad的学习率消失问题,与AdaGrad累积历史更新所不同的是,AdaDelta将过去的更新限制在固定的长度w里面。并且,由于存储过去w个更新在计算上效率很低,取而代之的是通过采取指数衰减的形式来保留最近的更新项(平方梯度)。
这里需要定义一个叫做均方根的概念,均方根的公式如下:
RMS[g]=sqrt(E(g^2)+epsilon)
简而言之,均方根就是平方均值的平方根。
AdaDelta的更新公式如下:
首先初始化两个均值,E[g^2]=0,E[d_param^2]=0
E[g^2]=rou*E[g^2]+(1-rou)*g^2
d_param=RMS[d_param]/RMS[g]*g
E[d_param^2]=rou*E[d_param^2]+(1-rou)*d_param^2
param=param-lr*d_param
其中rou为衰减率。
6:Adam
最近,Adam算法被提出来,该算法非常有效,并且只需要一阶梯度,而且对内存要求也很低。Adam同时考虑了梯度以及梯度的平方,因此,Adam同时具有AdaGrad和AdaDelta的优点,能够很好地适应于稀疏数据或不当的初始化网络。
Adam算法的更新公式如下:
初始化一阶向量m和二阶向量v为0;
设置最优的beta1、beta2的值(论文中有介绍实践最优默认值);
m=beta1*m+(1-beta1)*g
v=beta2*v+(1-beta2)*g^2
m=m/(1-beta1)
v=v/(1-beta2)
param=param-lr*m/(sqrt(v)+epsilon)







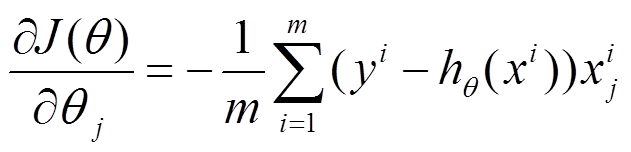
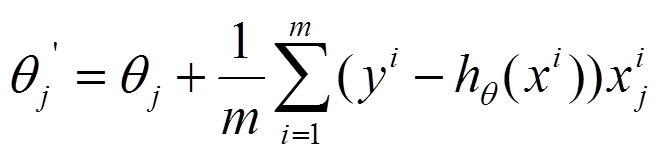
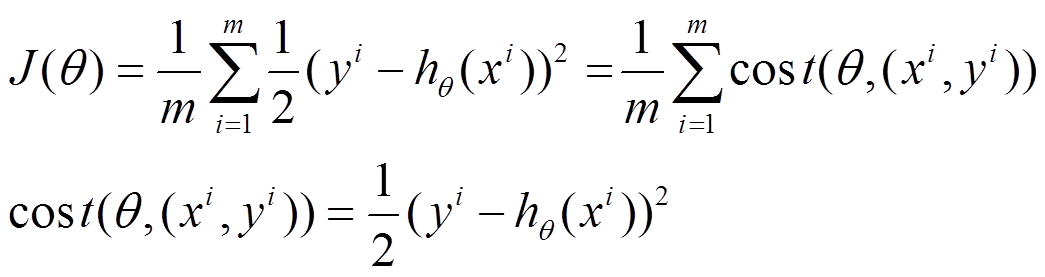















 544
544











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








